
1.(福建21)(1)(本小题满分7分)选修4-4:矩阵与变换 

已知矩阵M 所对应的线性变换把点A(x,y)变成点A ‘(13,5),试求M的逆矩阵及点A的坐标
所对应的线性变换把点A(x,y)变成点A ‘(13,5),试求M的逆矩阵及点A的坐标
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知直线l:3x+4y-12=0与圆C: (
( 为参数 )试判断他们的公共点个数
为参数 )试判断他们的公共点个数
(3)(本小题满分7分)选修4-5:不等式选讲
解不等式∣2x-1∣<∣x∣+1
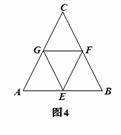
32. 解:(1)图中共有5个三角形;··········································· (2分)
(2)△ ≌△
≌△ . ·············································· (3分)
. ·············································· (3分)
∵ △ 是等边三角形,∴ ∠
是等边三角形,∴ ∠ ∠
∠ .···················· (4分)
.···················· (4分)
∵  、
、 、
、 是边
是边 、
、 、
、 的中点,
的中点,
∴AE=AG=CG=CF= AB. ····································································· (6分)
AB. ····································································· (6分)
∴ △ ≌△
≌△ . ········································································· (7分)
. ········································································· (7分)
31. (1)如图:
(2)证明 即可.
即可.
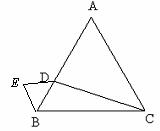
30. 解:(1)略.
(2)证明:∵BC=BD,点E是BC的中点,点F是BD的中点,
∴BE=BF.又∠ABC=∠ABD,AB=AB,∴△ABE≌△ABF.
29. 解:(1)如右图;
(2) .
.
理由:过 作
作 于
于 ,四边形
,四边形 为矩形,
为矩形, .
.
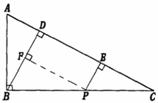
 ,
, ,
,
 .
.
在 和
和 中,
中,

 .
.
 .
.
 .
.
28. 证明:


∴在 和
和 中
中


27. 证明: ,
, ,
,
 ·················································································································· 1分
·················································································································· 1分
在 与
与 中
中
 ·········································· 2分
·········································· 2分


 ································································ 1分
································································ 1分

 1分
1分
26. 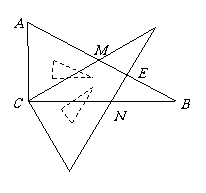 (1) 证明:∵∠A=∠A′ AC=A′C ∠ACM=∠A′CN=900-∠MCN
(1) 证明:∵∠A=∠A′ AC=A′C ∠ACM=∠A′CN=900-∠MCN
∴
(2)在Rt△ABC中
∵ ,∴∠A=900-300=600
,∴∠A=900-300=600
又∵ ,∴∠MCN=300,
,∴∠MCN=300,
∴∠ACM=900-∠MCN=600
∴∠EMB′=∠AMC=∠A=∠MCA=600
∵∠B′=∠B=300
所以三角形MEB′是Rt△MEB′且∠B′=300
所以MB′=2ME
25. 证明:(1)∵CF∥BE∴EBD=FCD
又∵∠BDE=∠CDF,BD=CD
∴△BDE≌△CDF
(2)四边形BECF是平行四边形
由△BDE≌△CDF得ED=FD
∵BD=CD
∴四边形BECF是平行四边形
24. (1) (或相等)
(或相等)
(2) (或成立),理由如下
(或成立),理由如下
方法一:由 ,得
,得


在 和
和 中
中



方法二、连接AD,同方法一, ,所以AF=DC。
,所以AF=DC。
由 。可证
。可证 。
。
(3)如图,
方法一:由 点B与点E重合,得
点B与点E重合,得 ,
,
所以点B在AD的垂直平分线上,
且

所以OA=OD,点O在AD的垂直平分线上,故 。
。
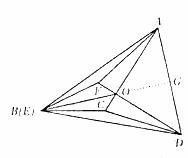
方法二:延长BO交AD于点G。同方法一OA=OD,可证
则 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com