23．(江苏卷)设变量x、y满足约束条件，则

的最大值为　　

[正确解答] 画出可行域，得在直线2x-y=2与直线x-y=-1的交点

A(3,4)处，目标函数z最大值为18

22．(湖南卷)已知则的最小值是　　　　 .

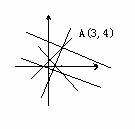解析：由，画出可行域，得交点A(1，2)，B(3，4)，则的最小值是5.

21．(湖北卷)若直线y＝kx+2与圆(x－2)²+(y－3)²＝1有两个不同的交点，则k 的取值范围是　　　 .

解：由直线y＝kx+2与圆(x－2)²+(y－3)²＝1有两个不同的交点可得直线与圆的位置关系是相交，故圆心到直线的距离小于圆的半径，即<1，解得kÎ(0，)

20．(湖北卷)已知直线与圆相切，则的值为　　　　 。

解：圆的方程可化为，所以圆心坐标为(1，0)，半径为1，由已知可得

，所以的值为－18或8。

19．(福建卷)已知实数、满足则的最大值是＿＿＿＿。

解析：已知实数、满足在坐标系中画出可行域，三个顶点分别是A(0，1)，B(1，0)，C(2，1)，∴ 的最大值是4.

18．(北京卷)已知点的坐标满足条件，点为坐标原点，那么的最小值等于_______,最大值等于____________.

解：画出可行域，如图所示：　　　　　　　　　　　　　　　　　　

易得A(2，2)，OA＝

B(1，3)，OB＝，，C(1，1)，OC＝

故|OP|的最大值为，最小值为.

17．(重庆卷)以点(2，－1)为圆心且与直线相切的圆的方程为

(A)　　 (B)

(C)　 (D)

解：r＝＝3，故选C

16．(重庆卷)过坐标原点且与x²+y² + 4x+2y+=0相切的直线的方程为

(A)y=-3x或y=x (B) y=-3x或y=-x　 (C)y=-3x或y=-x　 (B) y=3x或y=x　

解析：过坐标原点的直线为，与圆相切，则圆心(2，－1)到直线方程的距离等于半径，则，解得，∴ 切线方程为，选A.

15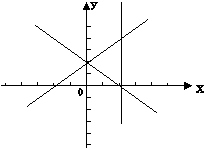．(浙江卷)在平面直角坐标系中，不等式组表示的平面区域的面积是

(A)　　　 (B)4　　　　　 (C) 　　　　　(D)2

[考点分析]本题考查简单的线性规划的可行域、三角形的面积。

解析：由题知可行域为，

　，故选择B。

14．(天津卷)设变量、满足约束条件，则目标函数的最小值为(　　 )

A．　　 　 　B．　　　 C．　　　　 D．

解析：设变量、满足约束条件在坐标系中画出可行域△ABC，A(2，0)，B(1，1)，C(3，3)，则目标函数的最小值为3，选B.