
13. 提示:(1)如图,AD即为所求。
(2)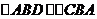 ,理由如下:
,理由如下:
AD平分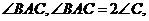 则
则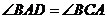 ,又
,又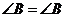 ,故
,故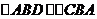 。
。
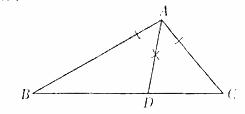
12. (1)证明:
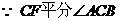 ,
,
∴ 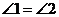 .
.
又∵ 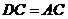 ,
,
∴ CF是△ACD的中线,
∴ 点F是AD的中点.
∵ 点E是AB的中点,
∴ EF∥BD,
即 EF∥BC.
(2)解:由(1)知,EF∥BD,
∴ △AEF∽△ABD ,
∴ 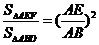 .
.
又∵ 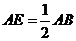 ,
,
 ,
,
∴ 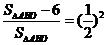 ,
,
∴ 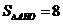 ,
,
∴ 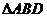 的面积为8.
的面积为8.
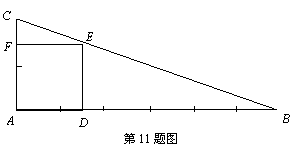
11. 解:⑴ 作图:作∠BAC的平分线交线段BC于E; …………………………………………………4分
 (痕迹清晰、准确,本步骤给满分4分,否则酌情扣1至4分;另外两点及边作的是否准确,不扣分)
(痕迹清晰、准确,本步骤给满分4分,否则酌情扣1至4分;另外两点及边作的是否准确,不扣分)
⑵ 如图,∵ 四边形ADEF是正方形,
∴ EF∥AB,AD = DE = EF = FA. ……5分
∴ △CFE ∽△CAB.
∴ 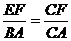 .…………………………………6分
.…………………………………6分
∵ AC = 2 ,AB = 6,
设AD = DE = EF = FA = x,
∴ 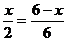 . ………………………………………………………………………………………………………7分
. ………………………………………………………………………………………………………7分
∴ x=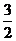 .即正方形ADEF的边长为
.即正方形ADEF的边长为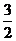 . ………………………………………………………………8分
. ………………………………………………………………8分
(本题可以先作图后计算,也可以先计算后作图;未求出AD或AF的值用作中垂线的方法找到D点或F点,给2分)
10. (1)∵△ABC为等腰三角形
∴AC=BC ∠CAB=∠CBA
又∵CH为底边上的高,P为高线上的点
∴PA=PB
∴∠PAB=∠PBA
∵∠CAE=∠CAB-∠PAB
∠CBF=∠CBA-∠PBA
∴∠CAE=∠CBF
(2)∵AC=BC
∠CAE=∠CBF
∠ACE=∠BCF
∴△ACE-△BCF(AAS)
∴AE=BF
(3)若存在点P能使S△ABC=S△ABG,因为AE=BF,所以△ABG也是一个等腰三角形,这两个三角形面积相等,底边也相同,所以高也相等,进而可以说明△ABC-△ABG,则对应边AC=AE,∠ACE=∠AEC,所以0°≤∠C<90°
9. [解] (1)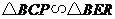 ,
,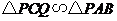 ,
,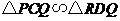 ,
,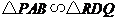 .
.
(2)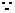 四边形
四边形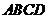 和四边形
和四边形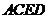 都是平行四边形,
都是平行四边形,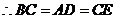 ,
,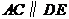 ,
,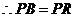 ,
,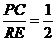 .又
.又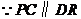 ,
,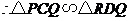 .
.
 点
点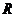 是
是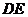 中点,
中点,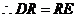 .
.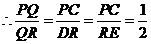 .
.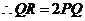 .
.
又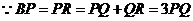 ,
,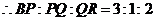 .
.
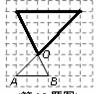
8.
7.
解:(1)∵MN∥BC,∴∠AMN=∠B,∠ANM=∠C.
∴ △AMN ∽ △ABC.
∴ 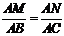 ,即
,即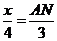 .
.
∴ AN=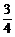 x. ……………2分
x. ……………2分
∴  =
=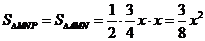 .(0<
.(0<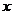 <4)
……………3分
<4)
……………3分
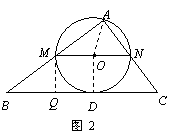 (2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =
(2)如图2,设直线BC与⊙O相切于点D,连结AO,OD,则AO =OD =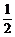 MN.
MN.
在Rt△ABC中,BC =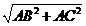 =5.
=5.
由(1)知 △AMN ∽ △ABC.
∴ 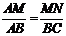 ,即
,即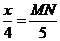 .
.
∴ 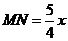 ,
,
∴ 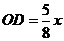 .
…………………5分
.
…………………5分
过M点作MQ⊥BC 于Q,则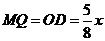 .
.
在Rt△BMQ与Rt△BCA中,∠B是公共角,
∴ △BMQ∽△BCA.
∴ 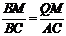 .
.
∴ 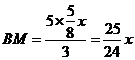 ,
,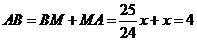 .
.
∴ x=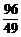 .
.
∴ 当x=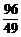 时,⊙O与直线BC相切.…………………………………7分
时,⊙O与直线BC相切.…………………………………7分
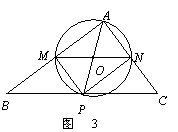 (3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
(3)随点M的运动,当P点落在直线BC上时,连结AP,则O点为AP的中点.
∵ MN∥BC,∴ ∠AMN=∠B,∠AOM=∠APC.
∴ △AMO ∽ △ABP.
∴ 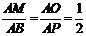 .
AM=MB=2.
.
AM=MB=2.
故以下分两种情况讨论:
① 当0<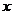 ≤2时,
≤2时,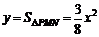 .
.
∴ 当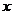 =2时,
=2时,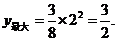 ……………………………………8分
……………………………………8分
② 当2<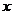 <4时,设PM,PN分别交BC于E,F.
<4时,设PM,PN分别交BC于E,F.
 ∵ 四边形AMPN是矩形,
∵ 四边形AMPN是矩形,
∴ PN∥AM,PN=AM=x.
又∵ MN∥BC,
∴ 四边形MBFN是平行四边形.
∴ FN=BM=4-x.
∴ 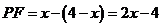 .
.
又△PEF ∽ △ACB.
∴ 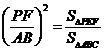 .
.
∴ 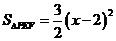 .
……………………………………………… 9分
.
……………………………………………… 9分
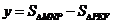 =
=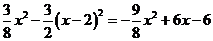 .……………………10分
.……………………10分
当2<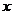 <4时,
<4时,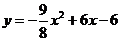
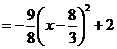 .
.
∴ 当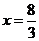 时,满足2<
时,满足2<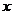 <4,
<4,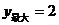 . ……………………11分
. ……………………11分
综上所述,当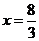 时,
时,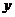 值最大,最大值是2. …………………………12分
值最大,最大值是2. …………………………12分
6. 解:(1)
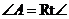 ,
,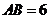 ,
,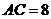 ,
,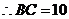 .
.
 点
点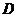 为
为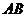 中点,
中点,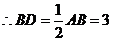 .
.
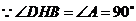 ,
,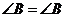 .
.
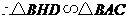 ,
,
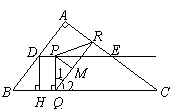
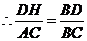 ,
,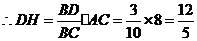 .
.
(2)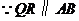 ,
,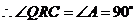 .
.
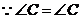 ,
,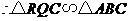 ,
,
 ,
,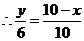 ,
,
即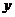 关于
关于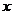 的函数关系式为:
的函数关系式为: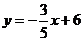 .
.
(3)存在,分三种情况:
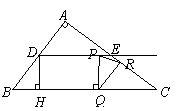 ①当
①当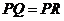 时,过点
时,过点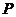 作
作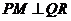 于
于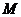 ,则
,则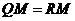 .
.
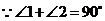 ,
,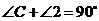 ,
,
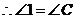 .
.
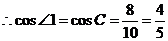 ,
,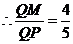 ,
,
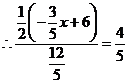 ,
,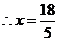 .
.
②当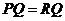 时,
时,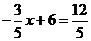 ,
,
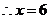 .
.
③当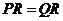 时,则
时,则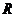 为
为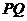 中垂线上的点,
中垂线上的点,
于是点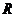 为
为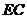 的中点,
的中点,
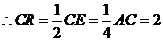 .
.
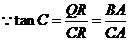 ,
,
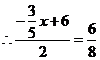 ,
,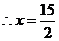 .
.
综上所述,当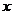 为
为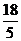 或6或
或6或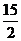 时,
时, 为等腰三角形.
为等腰三角形.
5. 解:(1)∆ABE∽∆DAE, ∆ABE∽∆DCA
∵∠BAE=∠BAD+45°,∠CDA=∠BAD+45°
∴∠BAE=∠CDA
又∠B=∠C=45°
∴∆ABE∽∆DCA
(2)∵∆ABE∽∆DCA
∴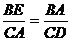
由依题意可知CA=BA=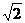
∴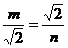
∴m=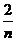
自变量n的取值范围为1<n<2.
(3)由BD=CE可得BE=CD,即m=n
∵m=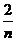
∴m=n=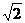
 ∵OB=OC=
∵OB=OC=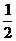 BC=1
BC=1
∴OE=OD=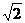 -1
-1
∴D(1-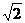 , 0)
, 0)
∴BD=OB-OD=1-(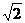 -1)=2-
-1)=2-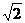 =CE,
DE=BC-2BD=2-2(2-
=CE,
DE=BC-2BD=2-2(2-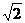 )=2
)=2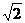 -2
-2
∵BD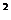 +CE
+CE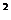 =2
BD
=2
BD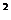 =2(2-
=2(2-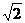 )
)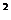 =12-8
=12-8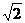 , DE
, DE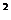 =(2
=(2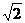 -2)
-2)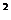 = 12-8
= 12-8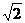
∴BD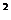 +CE
+CE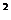 =DE
=DE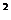
(4)成立
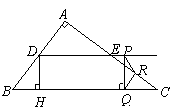
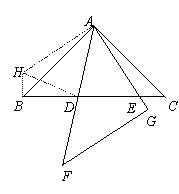
证明:如图,将∆ACE绕点A顺时针旋转90°至∆ABH的位置,则CE=HB,AE=AH,
∠ABH=∠C=45°,旋转角∠EAH=90°.
连接HD,在∆EAD和∆HAD中
∵AE=AH, ∠HAD=∠EAH-∠FAG=45°=∠EAD, AD=AD.
∴∆EAD≌∆HAD
∴DH=DE
又∠HBD=∠ABH+∠ABD=90°
∴BD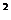 +HB
+HB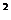 =DH
=DH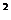
即BD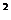 +CE
+CE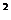 =DE
=DE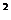
4. Ⅰ.证明:∵DEFG为正方形,
∴GD=FE,∠GDB=∠FEC=90°
∵△ABC是等边三角形,∴∠B=∠C=60°
∴△BDG≌△CEF(AAS)
Ⅱa.解法一:设正方形的边长为x,作△ABC的高AH,
求得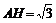
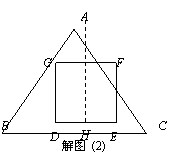 由△AGF∽△ABC得:
由△AGF∽△ABC得: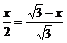
解之得: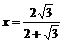 (或
(或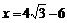 )
)
解法二:设正方形的边长为x,则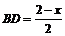
在Rt△BDG中,tan∠B=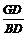 ,
,
∴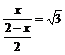
解之得: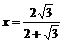 (或
(或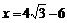 )
)
解法三:设正方形的边长为x,
则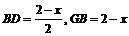
由勾股定理得: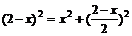
解之得: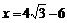
Ⅱb.解: 正确
由已知可知,四边形GDEF为矩形
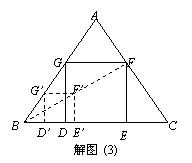 ∵FE∥F’E’ ,
∵FE∥F’E’ ,
∴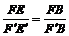 ,
,
同理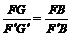 ,
,
∴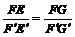
又∵F’E’=F’G’,
∴FE=FG
因此,矩形GDEF为正方形
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com