
1.(2002年全国理综,6)以下说法正确的是
A.纳米材料是指一种称为“纳米”的新物质制成的材料
B.绿色食品是指不含任何化学物质的食品
C.生物固氮是指植物通过叶面直接吸收空气中的氮气
D.光导纤维是以二氧化硅为主要原料制成的
3.凸n边形的内角和f(n)=(n-2)·180°(n≥3).
提示:(1)n=3时,图形是三角形,内角和为180°.
又f(3)=(3-2)·180°=180°.
∴n=3时命题成立.
(2)假设当n=k时,命题成立,即凸k边形的内角和为f(k)=(k-2)·180°,
那么n=k+1时,凸k+1边形的内角和是在原来的凸k边形的基础上增加一个三角形,内角和f(k)+180°=(k-2)·180°+180°=[(k+1)-2]·180°.
而f(k+1)=(k+1-2)·180°
∴n=k+1时,命题也成立.
由归纳假设凸n边形的内角和为f(n)=(n-2)·180°(n≥3).
2.xn-yn(n∈N*)能被x-y整除.
提示:(1)n=1时,x1-y1能被x-y整除.
(2)假设当n=k(k≥1)时命题成立,即xk-yk能被x-y整除.
那么n=k+1时,
xk+1-yk+1=x·xk-y·yk=x(xk-yk)+x·yk-y·yk=x(xk-yk)+yk(x-y).
由归纳假设xk-yk及x-y能被x-y整除,所以xk+1-yk+1能被x-y整除.
1.两个连续正整数的积能被2整除.
提示:设n∈N*,则要证明n(n+1)能被2整除.
(1)n=1时,1×(1+1)=2.能被2整除,即命题成立.
(2)假设n=k时,命题成立,即k·(k+1)能被2整除.
那么当n=k+1时,(k+1)(k+1+1)=(k+1)(k+2)=k(k+1)+2(k+1).
由归纳假设k(k+1)及2(k+1)都能被2整除.
∴(k+1)(k+2)能被2整除.故n=k+1时命题也成立
由(1)、(2)可知,命题对一切n∈N*都成立.
2. 平面内有n个圆,任意两个圆都相交于两点,任何三个圆都不相交于同一点,求证这n个圆将平面分成f(n)=n2-n+2个部分.
证明:(1)当n=1时,一个圆将平面分成两个部分,且f(1)=1-1+2=2.
因此,n=1时命题成立.
(2)假设n=k时命题成立,即k个圆把平面分成f(k)=k2-k+2个部分.
则n=k+1时,在k+1个圆中任取一个圆C,剩下的k个圆将平面分成f(k)个部分,而圆C与k个圆有2k个交点,这2k个交点将圆C分成2k段弧,每段弧将它所在的平面部分一分为二,故共增加了2k个平面部分,因此:f(k+1)=f(k)+2k=k2-k+2+2k=(k+1)2-(k+1)+2.
∴n=k+1时命题也成立.
由(1)、(2)知对一切n∈N*,命题都成立.
1.n为奇数时xn+yn能被x+y整除.
证明:(1)当n=1时,xn+yn=x+y,它能被x+y整除,所以n=1时命题成立.
(2) 假设当n=k(k为正奇数)时,命题成立,即xk+yk能被x+y整除.
当n=k+2时,
xk+2+yk+2=x2·xk+y2·yk=x2(xk+yk)+y2·yk-x2·yk
=x2(xk+yk)+yk(y2-x2)=x2(xk+yk)+yk·(y+x)(y-x).
由归纳假设知.xk+yk能被x+y整除.(y+x)(y-x)也能被x+y整除.
∴x2(xk+yk)+yk(y+x)(y-x)能被x+y整除.
即xk+2+yk+2也能被x+y整除.故对n=k+2时也成立.即第k+1个奇数也成立.
由(1)、(2)知命题对一切正奇数都成立
例1用数学归纳法证明:x2n-y2n (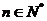 )能被x+y整除
)能被x+y整除
证明: (1)当n=1时,x2n-y2n=x2-y2=(x-y)(x+y)
所以(x-y)(x+y)能被x+y整除.故n=1时命题成立.
(2) 假设n=k时x2k-y2k能被x+y整除,
(利用添项去项将x2k+2-y2k+2配成x2k-y2k的形式,再用归纳假设)
因为x2k+2-y2k+2=x2·x2k-y2·y2k
=x2(x2k-y2k)+x2·y2k-y2·y2k
=x2(x2k-y2k)+y2k(x2-y2)
由假设x2k-y2k能被x+y整除,而x2-y2也能被x+y整除.
故x2k+2-y2k+2能被x+y整除,即n=k+1时也成立.
由(1)、(2)知命题对一切正整数都成立.
例2 用数学归纳法证明:对于任意自然数n,数11n+2+122n+1是133的倍数.
证明:(1) 当n=0时,11n+2+122n+1=112+121=121+12=133.故n=0时命题成立.
(2)假设当n=k时命题成立,即11k+2+122k+1能被133整除.
∴n=k+1时,
11(k+1)+2+122(k+1)+1=11·11k+2+122·122k+1
=11·(11k+2+122k+1)+122·122k+1-11×122k+1
=11·(11k+2+122k+1)+122k+1(144-11)
=11·(11k+2+122k+1)+122k+1·133
由归纳假设知11k+2+122k+1及133都能被133整除.
∴11(k+1)+2+122(k+1)+1能被133整除,即n=k+1时命题也成立.
根据(1)(2)可知.命题对一切自然数都成立.
说明:第一步的初始值,可能会:当n=1时,11n+2+122n+1=113+123=(11+12)(112-11×12+122)=23×(121+144-132)=23×133. ∴23×133能被133整除.即n=1时命题成立..因为自然数中包括0,所以第一步应验证n=0,而不是n=1.
本题第一步若证明n=1时命题成立,一者计算量较大,二者也不符合自然数集的新定义. 证n=0,既方便减少计算量又科学更严密.一般情况,有时为了简化计算常将证明n=1改证n=0或n=-1,这种技巧称之“提前起点”,提前起点的前提是n为整数,否则递推无法进行.另外,利用数学归纳法证明整除问题,由归纳假设P(k)能被p整除,证P(k+1)能被p整除,也可运用结论:“P(k+1)-P(k)能被p整除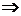 P(k+1)能被p整除.”
P(k+1)能被p整除.”
例3平面内有n(n≥2)条直线,其中任何两条不平行,任何三条不过同一点,证明交点的个数为f(n)= 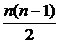 .
.
证明:(1)当n=2时,两条直线的交点只有一个,又f(2)=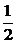 ×2×(2-1)=1,
×2×(2-1)=1,
因此,当n=2时,命题成立.
(2)假设当n=k(k≥2)时命题成立,就是说,平面内满足题设的任何k条直线的交点的个数f(k)等于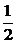 k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的一条直线,记为l.
k(k-1).现在来考虑平面内有k+1条直线的情况.任取其中的一条直线,记为l.
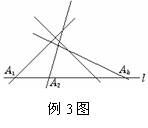 (如例3图所示).由上述归纳法的假设,除l以外的其他k条直线的交点个数为f(k)=
(如例3图所示).由上述归纳法的假设,除l以外的其他k条直线的交点个数为f(k)=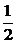 k(k-1).
k(k-1).
另外,因为已知任何两条直线不平行,所以直线l必与平面内其他k条直线都相交(有k个交点);又因为已知任何三条直线不过同一点,所以上面的k个交点两两不相同,且与平面内其他的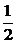 k·(k-1)个交点也两两不相同,从而平面内交点的个数是
k·(k-1)个交点也两两不相同,从而平面内交点的个数是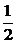 k(k-1)+k=
k(k-1)+k=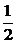 k[(k-1)+2]=
k[(k-1)+2]=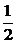 (k+1)[(k+1)-1].
(k+1)[(k+1)-1].
这就是说,当n=k+1时,k+1条直线的交点个数为
f(k+1)=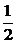 (k+1)[(k+1)-1].
(k+1)[(k+1)-1].
根据(1)、(2)可知命题对任何大于1的正整数都成立.
6.用数学归纳法证明一个与正整数有关的命题的步骤:
(1)证明:当n取第一个值n0结论正确;
(2)假设当n=k(k∈N*,且k≥n0)时结论正确,证明当n=k+1时结论也正确.
由(1),(2)可知,命题对于从n0开始的所有正整数n都正确 
递推基础不可少,归纳假设要用到,结论写明莫忘掉 .
. 
5. 数学归纳法的基本思想:即先验证使结论有意义的最小的正整数n0,如果当n=n0时,命题成立,再假设当n=k(k≥n0,k∈N*)时,命题成立.(这时命题是否成立不是确定的),根据这个假设,如能推出当n=k+1时,命题也成立,那么就可以递推出对所有不小于n0的正整数n0+1,n0+2,…,命题都成立.
4.数学归纳法:对于某些与自然数n有关的命题常常采用下面的方法来证明它的正确性:先证明当n取第一个值n0时命题成立;然后假设当n=k(kÎN*,k≥n0)时命题成立,证明当n=k+1时命题也成立 这种证明方法就叫做数学归纳法
这种证明方法就叫做数学归纳法
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com