
1.若集合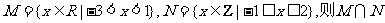 = ( )
= ( )
A.{0} B.{-1,0} C.{-1,0,1} D.{-2,-1,0,1,2}
22.(文)(本小题满分14分)已知函数f(x)=sin2x+2sin(x+)cos(x-)-cos2x-.
(1)求函数f(x)的最小正周期和单调递减区间;
(2)求函数f(x)在[-,π]上的最大值和最小值,并指出此时相应的x的值.
(理)(本小题满分14分)已知函数f(x)=2cosxsin(x+)-.
(1)求函数f(x)的最小正周期T;
(2)若△ABC的三边a,b,c满足b2=ac,且边b所对角为B,试求cosB的取值范围,并确定此时f(B)的最大值.
解:(1)f(x)=2cosx·sin(x+)-
=2cosx(sinxcos+cosxsin)-
=2cosx(sinx+cosx)-
=sinxcosx+·cos2x-
=sin2x+· -
=sin2x+cos2x
=sin(2x+).
∴T===π.
(2)由余弦定理cosB=得,cosB=
=-≥-=,∴≤cosB<1,
而0<B<π,∴0<B≤.函数f(B)=sin(2B+),
∵<2B+≤π,当2B+=,
即B=时,f(B)max=1.
21.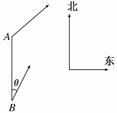 (本小题满分12分)如图所示,甲船由A岛出发向北偏东
(本小题满分12分)如图所示,甲船由A岛出发向北偏东
45°的方向做匀速直线航行,速度为15海里/小时,在甲
船从A岛出发的同时,乙船从A岛正南40海里处的B岛
出发,朝北偏东θ(tanθ=)的方向作匀速直线航行,速度
 为10海里/小时.
为10海里/小时.
(1)求出发后3小时两船相距多少海里?
(2)求两船出发后多长时间距离最近?最近距离为多少海里?
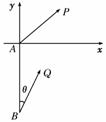
解:以A为原点,BA所在直线为y轴建立如图所示
的平面直角坐标系.
设在t时刻甲、乙两船分别在P(x1,y1),Q(x2,y2).
则,
由tanθ=可得,cosθ=,
sinθ=,
故
(1)令t=3,P、Q两点的坐标分别为(45,45),(30,20),
|PQ|===5.
即出发后3小时两船相距5海里.
(2)由(1)的解法过程易知:
|PQ|=
=
=
=≥20,
∴当且仅当t=4时,|PQ|取得最小值20.
即两船出发后4小时时,相距20海里为两船的最近距离.
20.(本小题满分12分)在△ABC中,角A,B,C的对边分别为a,b,c,cos=.
(1)求cosB的值;
(2)若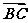
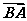 ·
·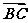 =2,b=2,求a和c的值.
=2,b=2,求a和c的值.
解:(1)∵cos=,
∴sin=sin(-)=,
∴cosB=1-2sin2=.
(2)由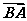 ·
·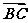 =2可得a·c·cosB=2,又cosB=,故ac=6,
=2可得a·c·cosB=2,又cosB=,故ac=6,
由b2=a2+c2-2accosB可得a2+c2=12,
∴(a-c)2=0,故a=c,∴a=c=.
19.(本小题满分12分)已知函数f(x)=2sinxcos(-x)-sin(π+x)cosx+sin(+x)cosx.
(1)求函数y=f(x)的最小正周期和最值;
(2)指出y=f(x)图象经过怎样的平移变换后得到的图象关于原点对称.
解:(1)f(x)=2sin2x+sinxcosx+cos2x
=1+sin2x+sinxcosx
=1++sin2x
=sin(2x-)+,
y=f(x)最小正周期T=π.
y=f(x)的最大值为+1=,最小值为-1=.
(2)∵y=+sin(2x-)的图象
 y=sin2x的图象.
y=sin2x的图象.
18.(文)(本小题满分12分)已知sin(π-α)=,α∈(0,).
(1)求sin2α-cos2的值;
(2)求函数f(x)=cosαsin2x-cos2x的单调递增区间.
解:∵sin(π-α)=,∴sinα=.
又∵α∈(0,),∴cosα=.
(1)sin2α-cos2
=2sinαcosα-
=2××-
=.
(2)f(x)=×sin2x-cos2x
=sin(2x-).
令2kπ-≤2x-≤2kπ+,k∈Z,
得kπ-≤x≤kπ+π,k∈Z.
∴函数f(x)的单调递增区间为[kπ-,kπ+π],k∈Z.
(理)(本小题满分12分)已知函数f(x)=2sinxcosx+(2cos2x-1).
(1)将函数f(x)化为Asin(ωx+φ)(ω>0,|φ|<)的形式,填写下表,并画出函数f(x)在区间[-π,π]上的图象;
|
x |
|
|
|
|
|
|
ωx+φ |
0 |
|
π |
π |
2π |
|
f(x) |
|
|
|
|
|

(2)求函数f(x)的单调减区间.
解:(1)f(x)=2sinxcosx+(2cos2x-1)
=sin2x+cos2x=2sin(2x+).
|
x |
- |
|
|
|
|
|
ωx+φ |
0 |
|
π |
π |
2π |
|
f(x) |
0 |
2 |
0 |
-2 |
0 |
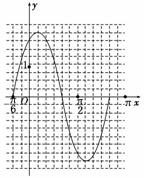 图.
图.
(2)由2kπ+≤2x+≤2kπ+(k∈Z)得
kπ+≤x≤kπ+(k∈Z),
故函数f(x)的单调减区间为[kπ+,kπ+](k∈Z).
17.(本小题满分12分)已知tan(α+)=-3,α∈(0,).
(1)求tanα的值;
(2)求sin(2α-)的值.
解:(1)由tan(α+)=-3可得=-3.
解得tanα=2.
(2)由tanα=2,α∈(0,),可得sinα=,cosα=.因此sin2α=2sinαcosα=,cos2α=1-2sin2α=-,sin(2α-)=sin2αcos-cos2αsin=×+×=.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com