
(15) 已知函数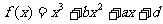 的图象过点P(0,2),且在点M
的图象过点P(0,2),且在点M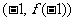 处的切线方程为
处的切线方程为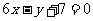 .
.
(Ⅰ)求函数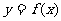 的解析式;
的解析式;
(Ⅱ)求函数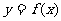 的单调区间.
的单调区间.
(16) 已知函数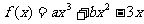 在
在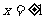 处取得极值.
处取得极值.
(Ⅰ)讨论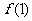 和
和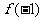 是函数
是函数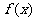 的极大值还是极小值;
的极大值还是极小值;
(Ⅱ)过点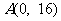 作曲线
作曲线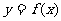 的切线,求此切线方程.
的切线,求此切线方程.
(17) 已知向量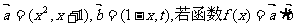 在区间(-1,1)上是增函数,求t的取值范围.
在区间(-1,1)上是增函数,求t的取值范围.
(18) 已知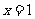 是函数
是函数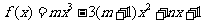 的一个极值点,其中
的一个极值点,其中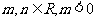 ,
,
(I)求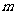 与
与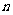 的关系式;
的关系式;
(II)求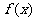 的单调区间;
的单调区间;
(III)(理科做)当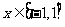 时,函数
时,函数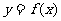 的图象上任意一点的切线斜率恒大于3
的图象上任意一点的切线斜率恒大于3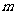 ,求
,求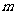 的取值范围.
的取值范围.
(11)设f(x)= x|x|, 则f′( 0)= .
(12)函数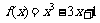 在闭区间[-3,0]上的最大值、最小值分别是
.
在闭区间[-3,0]上的最大值、最小值分别是
.
(13)若曲线y=h(x)在点P(a, h(a))处的切线方程为2x+y+1=0,则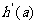 与0的大小关系是
与0的大小关系是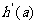 0
0
(14)过原点作曲线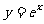 的切线,则切点的坐标为
,切线的斜率为 .
的切线,则切点的坐标为
,切线的斜率为 .
(1) 下列求导运算正确的是 ( )
A.(x+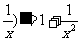 B.(log2x)′=
B.(log2x)′=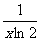
C.(3x)′=3xlog3e D. (x2cosx)′=-2xsinx
(2)
函数y=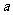 x2+1的图象与直线y=x相切,则
x2+1的图象与直线y=x相切,则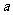 =
( )
=
( )
A. 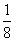 B.
B.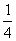 C.
C.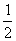 D.1
D.1
(3) 函数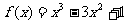 是减函数的区间为 ( )
是减函数的区间为 ( )
A.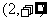 B.
B. C.
C. D.(0,2)
D.(0,2)
(4) 函数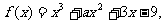 已知
已知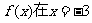 时取得极值,则
时取得极值,则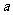 = ( )
= ( )
A.2 B.3 C.4 D.5
(5) 在函数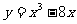 的图象上,其切线的倾斜角小于
的图象上,其切线的倾斜角小于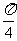 的点中,坐标为整数的点的个数是 ( )
的点中,坐标为整数的点的个数是 ( )
A.3 B.2 C.1 D.0
(6) 设f0(x) = sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x) = fn′(x),n∈N,则f2005(x)= ( )
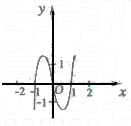 A.sinx B.-sinx C.cosx
D.-cosx
A.sinx B.-sinx C.cosx
D.-cosx
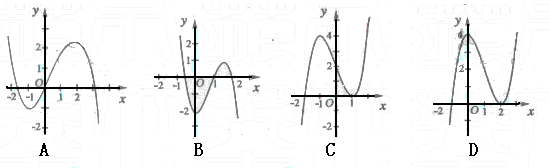
(7) 已知函数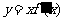 的图象如右图所示(其中
的图象如右图所示(其中 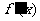 是函数
是函数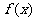 的导函数),下面四个图象中
的导函数),下面四个图象中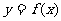 的图象大致是 ( )
的图象大致是 ( )
(8)设在[0, 1]上的函数f(x)的曲线连续, 且f′(x)>0, 则下列一定成立的是 ( )
A. f(0)<0 B. f(1)>0 C. f(1)> f(0) D. f(1)<f(0)
(9)设f(x)、g(x)分别是定义在R上的奇函数和偶函数,当x<0时, >0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
>0.且g(3)=0.则不等式f(x)g(x)<0的解集是 ( )
A. (-3,0)∪(3,+∞) B. (-3,0)∪(0, 3)
C. (-∞,- 3)∪(3,+∞) D. (-∞,- 3)∪(0, 3)
(10)若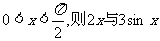 的大小关系
( )
的大小关系
( )
A.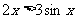 B.
B. C.
C.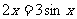 D.与x的取值有关
D.与x的取值有关
20、(04广西卷)(14分)一路灯距地面的高度为h,身高为l的人以速度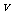 匀速行走,如图所示.
匀速行走,如图所示.
 (1)试证明人的头顶的影子作匀速运动;
(1)试证明人的头顶的影子作匀速运动;
(2)求人影的长度随时间的变化率.
(1)设t=0时刻,人位于路灯的正下方O处,
在时刻t,人走到S处,根据题意有
OS= ①
①
过路灯P和人头顶的直线与地面的交点M为t
时刻人头顶影子的位置,如图所示.OM为人头顶影子到O点的距离.
由几何关系,有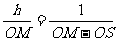 ②
②
解①②式得  ③
③
因OM与时间t成正比,故人头顶的影子作匀速运动.
(2)由图可知,在时刻t,人影的长度为SM,由几何关系,有SM=OM-OS ④
由①③④式得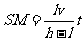 ⑤
⑤
可见影长SM与时间t成正比,所以影长随时间的变化率
 ⑥
⑥
19、(07全国理综Ⅰ)(15分)甲乙两运动员在训练交接棒的过程中发现:甲经短距离加速后能保持9 m/s的速度跑完全程;乙从起跑后到接棒前的运动是匀加速的,为了确定乙起跑的时机,需在接力区前适当的位置设置标记,在某次练习中,甲在接力区前S0=13.5 m处作了标记,并以V=9 m/s的速度跑到此标记时向乙发出起跑口令,乙在接力区的前端听到口令时起跑,并恰好在速度达到与甲相同时被甲追上,完成交接棒,已知接力区的长度为L=20 m。
求:⑴此次练习中乙在接棒前的加速度a。
⑵在完成交接棒时乙离接力区末端的距离。
解:⑴在甲发出口令后,,甲乙达到共同速度所用时间为:
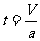
设在这段时间内甲、乙的位移分别为S1和S2,则:
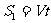

S1=S2+ S0
联立以上四式解得: 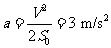
⑵在这段时间内,乙在接力区的位移为:
完成交接棒时,乙与接力区末端的距离为:L-S2=6.5 m
18.(08四川卷 理科)23.(16分)A、B两辆汽车在笔直的公路上同向行驶。当 B车在A车前84 m处时,B车速度为4 m/s,且正以2 m/s2的加速度做匀加速运动;经过一段时间后,B车加速度突然变为零。A车一直以20 m/s的速度做匀速运动。经过12 s后两车相遇。问B车加速行驶的时间是多少?
解析:23.( 6分)
设A车的速度为vA,B车加速行驶时间为t,两车在t0时相遇。则有
 ①
①
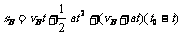 ②
②
式中,t0 =12s,sA、sB分别为 A、B两车相遇前行驶的路程。依题意有
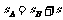 ③
③
式中 s=84 m。由①②③式得
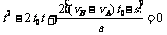 ④
④
代入题给数据
vA=20m/s,vB=4m/s,a =2m/s2,
有
 ⑤
⑤
式中矿的单位为s。解得
t1=6 s,t2=18 s ⑥
t2=18s不合题意,舍去。因此,B车加速行驶的时间为 6 s。
17. (08山东卷 理科) (2)一个物体静置于光滑水平面上,外面扣一质量为M的盒子,如图1所示。现给盒子一初速度v0,此后,盒子运动的v-t图象呈周期性变化,如图2所示。请据此求盒内物体的质量
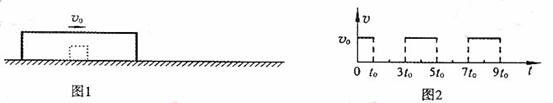
解析: (2)设物体的质量为m.t0时刻受盒子碰撞获得速度v,根据动量守恒定律
Mv0=mv ①
3t0时刻物体与盒子右壁碰撞使盒子速度又变为v0,说明碰撞是弹性碰撞
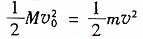 ②
②
联立①② 解得 m=M ③
(也可通过图象分析得出v0=v,结合动量守恒,得出正确结果)
16.(08全国I理科综合)23.(14分)已知O、A、B、C为同一直线上的四点、AB间的距离为l1,BC间的距离为l2,一物体自O点由静止出发,沿此直线做匀速运动,依次经过A、B、C三点,已知物体通过AB段与BC段所用的时间相等。求O与A的距离.
解析:23、(14分)
设物体的加速度为a,到达A的速度为v0,通过AB段和BC段所用的时间为t,则有
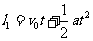 ……………………………………………①
……………………………………………①
 ………………………………………②
………………………………………②
联立①②式得
 …………………………………………………③
…………………………………………………③
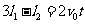 ………………………………………………④
………………………………………………④
设O与A的距离为 ,则有
,则有
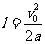 ………………………………………………………⑤
………………………………………………………⑤
联立③④⑤式得

15、(06江苏卷)17.下列情况中的速度,属于平均速度的是 ( B )
A.百米赛跑的运动员冲过终点线时的速度为9.5m/s
B.由于堵车,汽车在通过隧道过程中的速度仅为1.2m/s
C.返回地球的太空舱落到太平洋水面时的速度为8m/s D.子弹射到墙上时的速度为800m/s
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com