
17.(09四川绵阳)星期天,小明同学在父母的协助下,从早上七点开始每隔半小时对他家附近的气温和一个深水池里的水温进行测量,并根据记录的数据绘成温度-时间图象,如图所示。从图线可以看出乙的温度变化幅度小,是___ _(选填“气温”或“水温”)的图线,温度变化幅度小的原因是 。
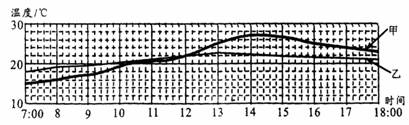
2.(09烟台)沿海地区同沙漠地区相比,冬暖夏凉,昼夜温差小.这是因为
A.水的密度比沙石的密度小 B.水的比热容大于沙石的比热容
C.水的热量大于沙石的热量 D.水的传热本领比沙石的传热本领差
答案:B
(09兰州). 由于水的比热容比沙石或干泥土的比热容大,所以在沿海地区陆地表面的气温比海面的气温昼夜变化显著。因此
A.白天的海风多是从陆地吹向海面,夜晚的海风多是从海面吹向陆地
B.白天的海风多是从海面吹向陆地,夜晚的海风多是从陆地吹向海面
C.白天和夜晚的海风多是从陆地吹向海面
D.白天和夜晚的海风多是从海面吹向陆地
答案:B
(09四川自贡).关于比热容,下列说法中正确的是
A.物体的比热容跟物体吸收和放出的热量有关
B.物体的比热容与物体的温度有关
C.物体的比热容与跟物体的质量有关
D.物体的比热容是物体的一种属性,与温度.质量都没有关系
答案:D
(09河北).根据表中几种物质的比热容,判断下列说法中不正确的是( )

A.制作体温计常用水银做介质,原因之一是水银的比热容小
B.北方楼房中的暖气用水做介质,利用了水的比热容大的特性
C.由于水比沙石的比热容大,所以内陆地区的昼夜温差比沿海地区大
D.由于水比冰的比热容大,所以冷却食品时0oC的水比0oC的冰效果好
答案:D
[解析]冷却食品时0oC的冰比0oC的水效果要好,原因是晶体熔化时吸热温度不变。
13.(09泰安)右图展示的是四川大凉山深处彝寨同学攀登木制云梯上学的情景,在攀登上升过程中,如果以 为参照物,可以判定其中一位同学是运动的;他的重力势能会 (选填“增大”、“不变”或“减小”)。
 答案:地面(或相对于地面静止的物体) 增大
答案:地面(或相对于地面静止的物体) 增大
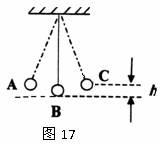
(09兰州).如图所示,把一个金属小球用细线悬挂起来,
将小球拉到A点,然后放开,小球在从A点运动至B
点的过程中,_______能转化为_______能。
答案:重力势 动
(09四川自贡).篮球比赛时,投入篮筐中的篮球从篮筐中下落过程中,篮球的 能转化为 能。
答案:重力势 动
13.(09重庆)许多同学都很喜欢设计和参加“多米诺骨牌效应”活动(按一定距离拌列的骨牌,碰倒第一块骨牌后,其它所有骨牌会依次倒下),其中的物理原理是:骨牌倒下时,
转化为 ,这部分能量就转移给下一张骨牌,下一张骨牌倒下时具有的能量更大,骨牌被推倒的速度越来越快。(选填“动能”、“重力势能”)
答案:重力势能 动能

22.已知函数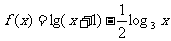 .
.
(Ⅰ)解关于x的方程: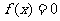 ;
;
(Ⅱ)记 ,
,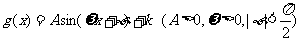 的最大、最小值构成的集合为
的最大、最小值构成的集合为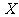 ,又
,又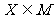 ,
,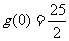 ,对于任意常数
,对于任意常数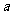 ,方程
,方程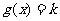 在区间
在区间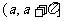 上有且只有两个根,试求函数
上有且只有两个根,试求函数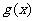 的单调增区间.
的单调增区间.
解:(Ⅰ)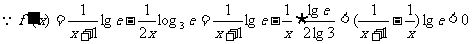
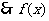 在
在 上递减;
上递减;
由于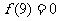 ,且
,且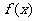 在
在 上递减;
上递减;
故: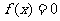 有且只有一个实数根
有且只有一个实数根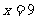 .
.
(Ⅱ)由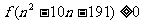 得:
得:
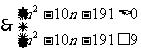 ;
;
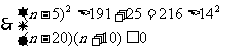 ;
;
 ;
;
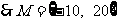 .
.
由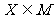 ,易知
,易知 ;
;
由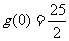 得
得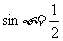 ,又
,又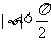 ,
,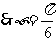 ;
;
由于方程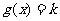 在区间
在区间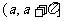 上有且只有两个根知
上有且只有两个根知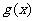 的最小正周期为
的最小正周期为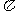 ,
,
 ;
;
从而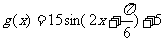 ;
;
由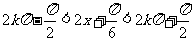 得
得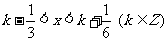 ;
;
故函数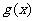 的单调增区间
的单调增区间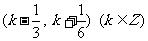 .
.
21.已知直线l与抛物线 相切于点
相切于点 ,又与抛物线
,又与抛物线 相交于两点A、B. 分别过A、B作
相交于两点A、B. 分别过A、B作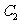 的切线
的切线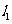 ,
,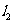 相交于点Q,设
相交于点Q,设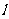 ,
,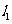 ,
,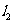 的斜率分别为
的斜率分别为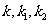 .
.
求证:(Ⅰ)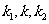 成等差数列;
成等差数列;
(Ⅱ)点Q在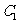 上.
上.
证明:(Ⅰ)设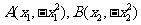 ,
,
对 求导得
求导得 ;
; ,
,
所以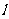 的方程为
的方程为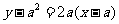 ,即
,即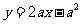 ,代入
,代入 得
得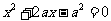 ,
,
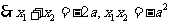 .
.
对 求导得
求导得 ;
; ,
, ;
;
从而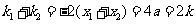 ,
,
所以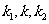 成等差数列;
成等差数列;
(Ⅱ)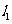 的方程为
的方程为 ,即
,即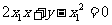 ,
,
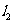 的方程为
的方程为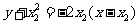 ,即
,即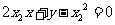 ,
,
两式相减得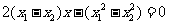 ,
,
即 ,
,
将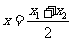 代入
代入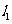 的方程得
的方程得 ,
,
即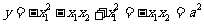 ,
,
所以点Q的坐标为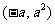 ,显然满足
,显然满足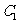 的方程,
的方程,
故点Q在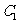 上.
上.
20. 设函数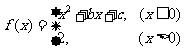 其中
其中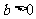 ,
,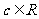 .当且仅当
.当且仅当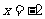 时,函数
时,函数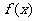 取得最小值
取得最小值 .
.
(Ⅰ)求函数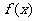 的表达式;
的表达式;
(Ⅱ)若方程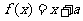
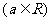 至少有两个不相同的实数根,求
至少有两个不相同的实数根,求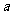 取值的集合.
取值的集合.
解:(Ⅰ)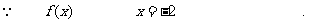


(Ⅱ)记方程①: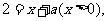 方程②:
方程②:
分别研究方程①和方程②的根的情况:
(1)方程①有且仅有一个实数根 方程①没有实数根
方程①没有实数根
(2)方程②有且仅有两个不相同的实数根,即方程 有两个不相同的非正实数根.
有两个不相同的非正实数根.

方程②有且仅有一个不相同的实数根,即方程 有且仅有一个蜚 正实数根.
有且仅有一个蜚 正实数根.

综上可知:当方程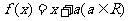 有三个不相同的实数根时,
有三个不相同的实数根时,
当方程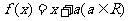 有且仅有两个不相同的实数根时,
有且仅有两个不相同的实数根时,
 符合题意的实数
符合题意的实数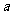 取值的集合为
取值的集合为
18. 已知函数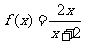 ,定义数列
,定义数列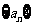 ,使:
,使: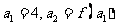 ,…,
,…,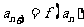 … .
… .
(1)求证:数列 是等差数列;
是等差数列;
(2)设数列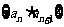 的前n项和为
的前n项和为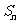 ,求证:
,求证: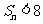 .
.
解:(1)∵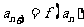 ∴
∴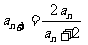
∴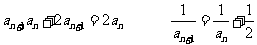
又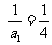 ∴数列{
∴数列{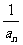 }是以
}是以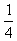 为首项,以
为首项,以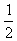 为公差的等差数列.
为公差的等差数列.
(2)由(1)可知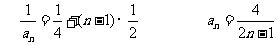
∴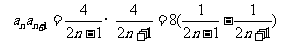
∴
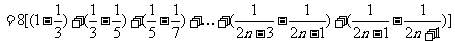
 .
.
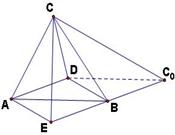
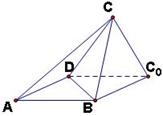 19:如图,一张平行四边形的硬纸片
19:如图,一张平行四边形的硬纸片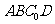 中,
中, ,
,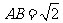 .沿它的对角线
.沿它的对角线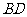 把
把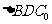 折起,使点
折起,使点 到达平面
到达平面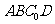 外点
外点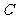 的位置.
的位置.
(Ⅰ)证明:平面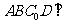 平面
平面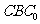 ;
;
(Ⅱ)如果△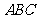 为等腰三角形,求二面角
为等腰三角形,求二面角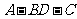 的大小。
的大小。
解:(Ⅰ)证明:因为 ,
,
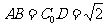 ,所以
,所以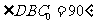 .
.
因为折叠过程中,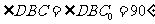 ,
,
所以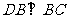 ,又
,又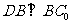 ,故
,故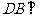 平面
平面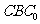 .
.
又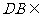 平面
平面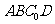 ,
,
所以平面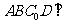 平面
平面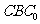 .
.
(Ⅱ)解法一:如图,延长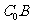 到
到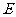 ,使
,使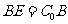 ,连结
,连结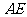 ,
, 。
。
因为

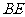 ,
,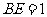 ,
,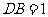 ,
,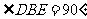 ,所以
,所以 为正方形,
为正方形,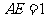 。
。
 由于
由于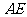 ,
,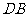 都与平面
都与平面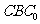 垂直,所以
垂直,所以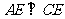 ,可知
,可知 。
。
因此只有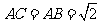 时,△
时,△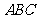 为等腰三角形。
为等腰三角形。
在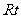 △
△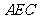 中,
中,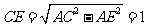 ,又
,又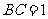 ,
,
所以△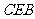 为等边三角形,
为等边三角形,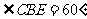 。
。
由(Ⅰ)可知,,所以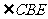 为二面角
为二面角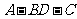 的平面角,即二面角
的平面角,即二面角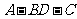 的大小为
的大小为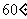 。
。
解法二:以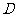 为坐标原点,射线
为坐标原点,射线 ,
,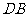 分别为
分别为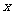 轴正半轴和
轴正半轴和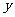 轴正半轴,建立如图的空间直角坐标系
轴正半轴,建立如图的空间直角坐标系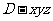 ,则
,则 ,
,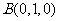 ,
,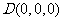 。
。
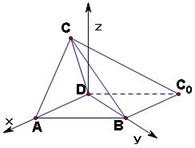 由(Ⅰ)可设点
由(Ⅰ)可设点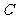 的坐标为
的坐标为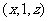 ,其中
,其中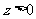 ,则有
,则有 。 ①
。 ①
因为△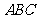 为等腰三角形,所以
为等腰三角形,所以 或
或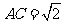 。
。
若 ,则有
,则有 。
。
则此得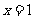 ,
,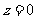 ,不合题意。
,不合题意。
若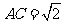 ,则有
,则有 。
②
。
②
联立①和②得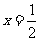 ,
,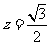 。故点
。故点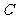 的坐标为
的坐标为 。
。
由于 ,
,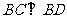 ,所以
,所以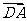 与
与 夹角的大小等于二面角
夹角的大小等于二面角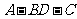 的大小。
的大小。
又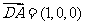 ,
, ,
,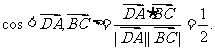
所以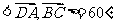 即二面角
即二面角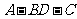 的大小为
的大小为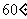 。
。
17.已知△ABC的周长为6,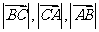 成等比数列.
成等比数列.
(Ⅰ)求 角B及边b的取值范围;
(Ⅱ)求△ABC的面积S的最大值及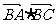 的取值范围.
的取值范围.
解:(Ⅰ)设 依次为
依次为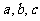 ,则
,则 ,
, ,
,
由余弦定理得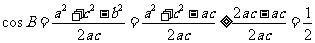 ,
,
故有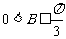 ,
,
又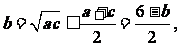 从而
从而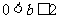 ;
;
(Ⅱ)所以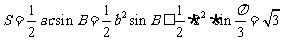 ,即
,即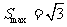
所以

 .
.
16、关于函数 (
(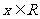 ,且常数
,且常数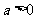 )对于下列命题:
)对于下列命题:
①函数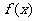 的最小值为-2;
的最小值为-2;
②函数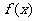 在每一点处都连续;
在每一点处都连续;
③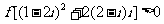 ;
;
④函数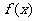 在
在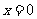 处可导;
处可导;
⑤对任意的实数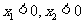 且
且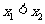 ,恒有
,恒有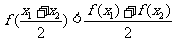
其中正确命题的序号是___________________ (②③⑤)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com