
3. 设a, b,
c是的△ABC三边,S是三角形的面积,求证: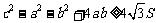 .
.
略证:正弦、余弦定理代入得: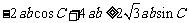 ,
,
即证: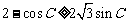 ,即:
,即: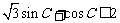 ,即证:
,即证: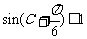 (成立).
(成立).
作业:教材P54 A组 1题.
2. 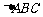 的三个内角
的三个内角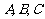 成等差数列,求证:
成等差数列,求证: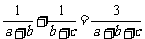 .
.
1. 求证:对于任意角θ,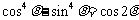 . (教材P52 练习 1题)
. (教材P52 练习 1题)
(两人板演 → 订正 → 小结:运用三角公式进行三角变换、思维过程)
3. 证明:通过水管放水,当流速相等时,如果水管截面(指横截面)的周长相等,那么截面的圆的水管比截面是正方形的水管流量大 .
.
提示:设截面周长为l,则周长为l的圆的半径为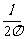 ,截面积为
,截面积为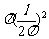 ,周长为l的正方形边长为
,周长为l的正方形边长为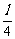 ,截面积为
,截面积为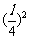 ,问题只需证:
,问题只需证: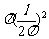 >
> 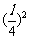 .3. 小结:综合法是从已知的P出发,得到一系列的结论
.3. 小结:综合法是从已知的P出发,得到一系列的结论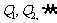 ,直到最后的结论是Q.
运用综合法可以解决不等式、数列、三角、几何、数论等相关证明问题. 分析法由要证明的结论Q思考,一步步探求得到Q所需要的已知
,直到最后的结论是Q.
运用综合法可以解决不等式、数列、三角、几何、数论等相关证明问题. 分析法由要证明的结论Q思考,一步步探求得到Q所需要的已知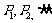 ,直到所有的已知P都成立;
,直到所有的已知P都成立;
比较好的证法是:用分析法去思考,寻找证题途径,用综合法进行书写;或者联合使用分 析法与综合法,即从“欲知”想“需知”(分析),从“已知”推“可知”(
析法与综合法,即从“欲知”想“需知”(分析),从“已知”推“可知”( 综合
综合 ),双管齐下,两面夹击,逐步缩小条件与结论之间的距离,找到沟通已知条件和结论的途径. (框图示意)
),双管齐下,两面夹击,逐步缩小条件与结论之间的距离,找到沟通已知条件和结论的途径. (框图示意)
2. 已知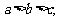 求证:
求证: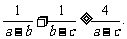
1.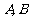 为锐角,且
为锐角,且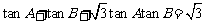 ,求证:
,求证: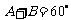 . (提示:算
. (提示:算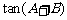 )
)
2. 练习:
1. 教学例题:
(1).出示例1:已知a, b, c是不全相等的正数,求证:a(b2 + c2) + b(c2 + a2) + c(a2 + b2) > 6abc.
分析:运用什么知识来解决?(基本不等式) → 板演 证明过程(注意等号的处理)
证明过程(注意等号的处理)
→ 讨论:证明形 式的特点
式的特点
(2).提出综合法:利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立.
 框图表示:
框图表示: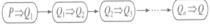 要点:顺推证法;由因导果.
要点:顺推证法;由因导果.
(3) .练习:已知a,b,c是全不相等的正实数,求证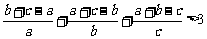 .
.
(4) .出示例2:在△ABC中,三个内角A、B、C的对边分别为a、b、c,且A、B、C成等差数列,a、b、c成等比数列. 求证:为△ABC等边三角形.
分析:从哪些已知,可以得到什么结论? 如何转化三角形中边角关系?
→ 板演证明过程 → 讨论:证明过程的特点.
→ 小结:文字语言转化为符号语言;边角关系的转化;挖掘题中的隐含条件(内角和)
(5). 出示例3:求证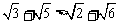 .
.
讨论:能用综 合法证明吗?
→ 如何从结论出发,寻找结论成立的充分条件?
合法证明吗?
→ 如何从结论出发,寻找结论成立的充分条件?
→ 板演证明过程 (注意格式)
→ 再讨论:能用综合法证明吗? → 比较:两种证法
(6).提出分析法:从要证明的结论出发,逐步寻找使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定理、定义、公理等)为止.
框图表示: 要点:
要点: 逆推证法;执果索因.
逆推证法;执果索因.
(7). 练习:设x > 0,y > 0,证明不等式: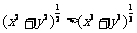 .
.
先讨论方法 → 分别运用分析法、综合法证明.
(8). 出示例4:见教材P48. 讨论:如何寻找证明思路?(从结论出发,逐步反推)
(9).  出示例5:见教材P49. 讨论:如何寻找证明思路?(从结论与已知出发,逐步探求)
出示例5:见教材P49. 讨论:如何寻找证明思路?(从结论与已知出发,逐步探求)
4. 讨论:如何证明基本不等式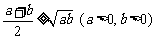 .
.
(讨论 → 板演 →
分析思维特点:从结论出发,一步步探求结论成立的充分条件)
→
分析思维特点:从结论出发,一步步探求结论成立的充分条件)
3. 提问:基本不等式的形式?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com