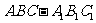16. 如图，斜三棱柱，已知侧面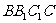与底面ABC垂直且∠BCA=90°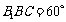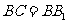，∠，=2，若二面角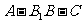为30°，　　

(Ⅰ)证明；　　　　　　　　　　　　

(Ⅱ)求与平面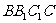所成角的正切值；

(Ⅲ)在平面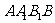内找一点P，使三棱锥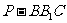为正三棱锥，并求P到平面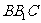距离

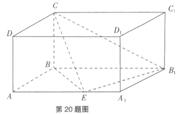
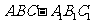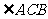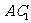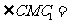15.如图所示，已知直三棱柱中，＝90^o，侧面与侧面所成的二面角为60°，M为上的点，30°，90°，．

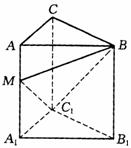
　(1)求BM与侧面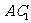所成角的正切值；

(2)求顶点A到面的距离．

14.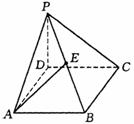 如图所示，PD垂直于正方形ABCD所在平面，AB＝2，E是PB的中点，与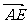夹角的余弦值为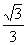

　(1)建立适当的空间坐标系，写出点E的坐标；

　(2)在平面PAD内求一点F，使EF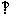平面PCB．

13. 已知正三棱柱ABC-A₁B₁C₁的底边长为1，高为h(h>3)，点M在侧棱BB₁上移动，到底面ABC的距离为x，且AM与侧面BCC₁所成的角为α；

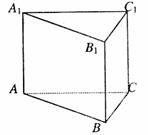　 　 (Ⅰ)(本问6分)若α在区间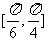上变化，求x的变化范围；

　 (Ⅱ)(本问6分)若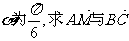所成的角.

12. 已知长方体ABCD-A₁B₁C₁D₁中，E为AA₁上一点，平面B₁CE⊥平面BCE，AB=BC=1，AA₁=2。

(1)求平面B₁CE与平面B₁BE所成二面角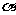的大小；(文科只要求求tan)

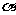(2)求点A到平面B₁CE的距离。

11. 如图，在正方体ABCD-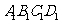中，E、F分别是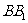，CD的中点．

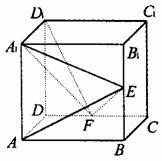　(1)证明：AD⊥；

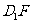　(2)求AE与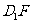所成的角；

　(3)证明：面AED⊥面；

　(4)设＝2，求三棱锥F-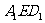的体积．

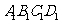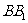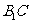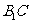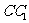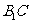10. 已知长方体ABCD-中，棱AB＝BC＝3，＝4，连结，过B点作的垂线交于E，交于F．

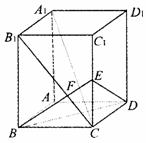
　(1)求证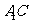：⊥平面EBD；

　(2)求ED与平面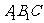所成角的大小；

　(3)求二面角E-BD-C的大小．

9. 如图，以正四棱锥V-ABCD底面中心O为坐标原点建立空间直角坐标系O-xyz，其中Ox∥BC，Oy∥AB，E为VC中点，正四棱锥底面边长为2a，高为h．

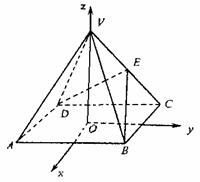
(1)求cos(，)；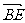

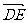(2)记面BCV为 ，面DCV为，若∠BED是二面角VC-的平面角，求∠BED．

8. 如图．已知斜三棱柱ABC-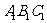的各棱长均为2，侧棱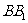与底面ABC所成角为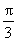，且侧面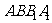垂直于底面ABC．

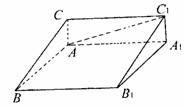(1)求证：点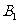在平面ABC上的射影为AB的中点；

(2)求二面角C--B的大小；

(3)判断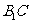与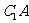是否垂直，并证明你的结论．

7. 如图，已知正四棱柱的底面边长为3，侧棱长为4，连结，过A作，垂足为F，且AF的延长线交于E。

　　 (I)求证：平面AEC

　　 (II)求三棱锥的体积

　　 (III)求二面角的正切值。