
2.会测量加速度、力、质量;并能作出表示加速度与力、加速度与质量的关系的图象;能根据图象写出加速度与力、质量的关系式。
1.能独立设计探究加速度、质量、力三者关系的探究方案。
1.自我认知 穷人:很少想到如何去赚钱和如何才能赚到钱,认为自己一辈子就该这样,不相信会有什么改变。 富人:骨子里就深信自己生下来不是要做穷人,而是要做富人,他有强烈的赚钱意识,这已是他血液里的东西,他会想尽一切办法使自己致富。 2.休闲 穷人:在家看电视,为肥皂剧的剧情感动得痛哭流涕,还要仿照电视里的时尚打扮自己。 富人:在外跑市场,即使打高尔夫球也不忘带着项目合同。 3.交际圈子 穷人:喜欢走穷亲戚,穷人的圈子大多是穷人,也排斥与富人交往,久而久之,心态成了穷人的心态,思维成了穷人的思维,做出来的事也就是穷人的模式。大家每天谈论着打折商品,交流着节约技巧,虽然有利于训练生存能力,但你的眼界也就渐渐囿于这样的琐事,而将雄心壮志消磨掉了。 富人:最喜欢交那种对自己有帮助,能提升自己各种能力的朋友。不纯粹放任自己,仅以个人喜好交朋友。 4.学习 穷人:学手艺。 富人:学管理。 5.时间 穷人:一个享受充裕时间的人不可能挣大钱,要想悠闲轻松就会失去更多挣钱的机会。穷人的时间不值钱的,有时甚至多余,不知道怎么打发,怎么混起来才不烦。如果你可以因为买一斤白菜多花了一毛钱而气恼不已,却不为虚度一天而心痛,这就是典型的穷人思维。 富人:一个人无论以何种方式挣钱,也无论钱挣得是多是少,都必须经过时间的积淀。富人的玩也是一种工作方式,是有目的的。富人的闲,闲在身体,修身养性,以利再战,脑袋一刻也没有闲着;穷人的闲,闲在思想,他手脚都在忙,忙着去麻将桌上多摸几把。 6.归属感 穷人:是颗螺丝钉。穷人因为自身的卑微,缺少安全感,就迫切地希望自己从属并依赖于一个团体。于是他们以这个团体的标准为自己的标准,让自己的一切合乎规范,为团体的利益而工作,奔波,甚至迁徙。对于穷人来说,在一个著名的企业里稳定地工作几十年,由实习生一直干到高级主管,那简直是美妙得不能再美妙的理想了。 富人:那些团体的领导者通常都是富人,他们总是一方面向穷人灌输:团结就是力量,如果你不从属于自己这个团体,你就什么都不是,一文不名。但另一方面,他们却从来没有停止过招兵买马,培养新人,以便随时可以把你替换。 7.投资及对待财富 穷人:经典观点就是少用就等于多赚。比如开一家面馆,收益率是100%,投入2万,一年就净赚2万,对穷人来说很不错了。穷人即使有钱,也舍不得拿出来,即使终于下定决心投资,也不愿冒风险,最终还是走不出那一步。穷人最津津乐道的就是鸡生蛋,蛋生鸡,一本万利……但是建筑在一只母鸡身上的希望,毕竟是那样脆弱。 富人:富人的出发点是万本万利。同样的开面馆,富人们会想,一家面馆承载的资本只有2万,如果有1亿资金,岂不是要开5000家面馆?要一个一个管理好,大老板得操多少心,累白多少根头发呀?还不如投资宾馆,一个宾馆就足以消化全部的资本,哪怕收益率只有20%,一年下来也有2000万利润啊! 8.激情 能不能干成大事,首先要看有没有激情。 穷人:没有激情。他总是按部就班,很难出大错,也绝不会做最好。没有激情就无法兴奋,就不可能全心全意投入工作,大部分的穷人不能说没有激情,但他的激情总是消耗在太具体的事情上;上司表扬了,他会激动;商店打折了,他会激动;电视里破镜重圆了,他的眼泪一串一串往下流,穷人有的只是一种情绪。 富人:“燕雀安知鸿鹄之志?”“王侯将相,宁有种乎?”有这样的激情,穷人终将不是穷人!激情是一种天性,是生命力的象征,有了激情,才有了灵感的火花,才有了鲜明的个性,才有了人际关系中的强烈感染力,也才有了解决问题的魅力和方法。 9.自信 穷人:穷人的自信要通过武装到牙齿,要通过一身高级名牌的穿戴和豪华的配饰才能给他们带来更多的自信,穷人的自信往往不是发自内心和自然天成的。 富人:李嘉诚在谈到他的经营秘诀时说:“其实也没什么特别的,光景好时,决不过分乐观;光景不好时,也不过度悲观”。其实就是一种富人特有的自信。自信才能不被外力所左右,自信才可能有正确的决定。 10.习惯 穷人:有个故事,一个富人送给穷人一头牛。穷人满怀希望开始奋斗。可牛要吃草,人要吃饭,日子很难。穷人于是把牛卖了,买了几只羊,吃了一只,剩下的来生小羊。可小羊迟迟没有生下来,日子又艰难了。穷人又把羊卖了,买成鸡。想让鸡生蛋赚钱为生,但是日子并没有改变,最后穷人把鸡也杀了,穷人的理想彻底崩溃了。这就是穷人的习惯。 富人:据一个投资专家说,富人成功秘诀就是:没钱时,不管多困难,也不要动用投资和积蓄,压力使你找到赚钱的新方法,帮你还清账单。这是个好习惯。性格形成习惯,习惯决定成功。 11.上网络 穷人:上网聊天。穷人聊天,一是穷人时间多,二是穷人的嘴天生就不能闲着。富人讲究荣辱不惊,温柔敦厚,那叫涵养,有涵养才能树大根深。穷人就顾不了那么多,成天受着别人的白眼,浑身沾满了鸡毛蒜皮,多少窝囊气啊,说说都不行?聊天有理! 富人:上网找投资机会。富人上网,更多的是利用网络的低成本高效率,寻找更多的投资机会和项目,把便利运用到自己的生意中来。 12.消费花钱 穷人:买名牌是为了体验满足感,最喜欢试验刚出来的流行时尚产品,相信贵的必然是好的。 富人:买名牌是为了节省挑选细节的时间,与消费品的售价相比,他们更在乎产品的质量,比如会买15元的纯棉T恤,也不会买昂贵的莱卡制品。
5. 自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能
力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.
不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,
这些比例系数依次为正常数a,b,c.
(1)求xn+1与xn的关系式;
(2)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?
(3)设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的
最大允许值是多少?证明你的结论.
4.已知不等式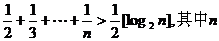 为大于2的整数,
为大于2的整数, 表示不超过
表示不超过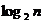 的最大整数. 设数列
的最大整数. 设数列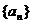 的各项为正,且满足
的各项为正,且满足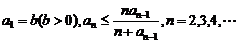 证明
证明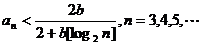 .
.
3.已知数列
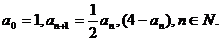
证明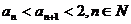 .
.
2.已知数列{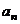 }的前n项和
}的前n项和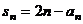 ,则{
,则{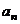 }的前四项依次为_______,猜想
}的前四项依次为_______,猜想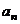 =__________.
=__________.
1.用数学归纳法证明等式“1+2+3+…+(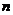 +3)=
+3)=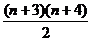 (
(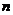
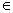 N)”,
N)”,
当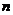 =1时,左边应为____________.
=1时,左边应为____________.
[例1] {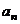 }是正数组成的数列,其前n项和为
}是正数组成的数列,其前n项和为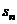 ,并且对于所有的自然数
,并且对于所有的自然数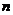 ,
,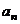 与2的等差中项等于
与2的等差中项等于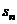 与2的等比中项.
与2的等比中项.
(1)写出数列{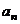 }的前3项;
}的前3项;
(2)求数列{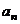 }的通项公式(写出推证过程);
}的通项公式(写出推证过程);
错解:由(1)猜想数列{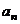 }有通项公式
}有通项公式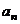 =4
=4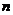 -2.
-2.
下面用数学归纳法证明数列{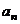 }的通项公式是
}的通项公式是
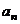 =4
=4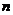 -2. (
-2. (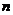 ∈N).
∈N).
①当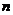 =1时,因为4×1-2=2,又在(1)中已求出
=1时,因为4×1-2=2,又在(1)中已求出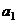 =2,所以上述结论成立.
=2,所以上述结论成立.
②假设n=k时结论成立,即有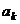 =4
=4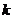 -2.由题意,有
-2.由题意,有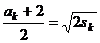
将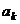 =4
=4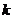 -2代入上式,得
-2代入上式,得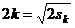 ,解得
,解得
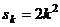
由题意,有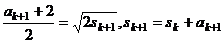
将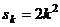 代入,化简得
代入,化简得
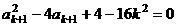
解得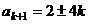 .∴
.∴
这就是说,当n=k+1时,上述结论成立.
根据①、②,上述结论对所有的自然数n成立.
错因在于解题过程中忽视了取值的取舍.
正解:由(1)猜想数列{an}有通项公式an=4n-2.
猜想数列{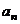 }有通项公式
}有通项公式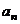 =4
=4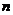 -2.
-2.
下面用数学归纳法证明数列{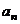 }的通项公式是
}的通项公式是
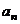 =4
=4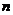 -2. (
-2. (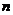 ∈N).
∈N).
①当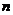 =1时,因为4×1-2=2,又在(1)中已求出
=1时,因为4×1-2=2,又在(1)中已求出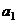 =2,所以上述结论成立.
=2,所以上述结论成立.
②假设n=k时结论成立,即有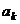 =4
=4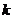 -2.由题意,有
-2.由题意,有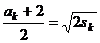
将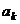 =4
=4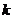 -2代入上式,得
-2代入上式,得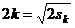 ,解得
,解得
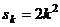
由题意,有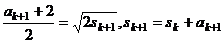
将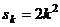 代入,化简得
代入,化简得
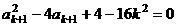
解得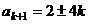 .由
.由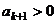 ∴
∴
这就是说,当n=k+1时,上述结论成立.
根据①、②,上述结论对所有的自然数n成立.
[例2] 用数学归纳法证明对于任意自然数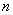 ,
,
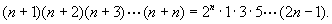
错解:证明:假设当 (
(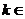 N)时,等式成立,
N)时,等式成立,
即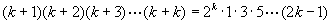 ,
,
那么当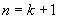 时,
时,
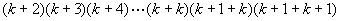
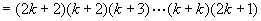
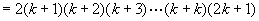
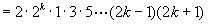
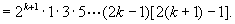
这就是说,当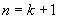 时,等式成立.
时,等式成立.
可知等式对任意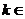 N成立.
N成立.
错因在于推理不严密,没有证明当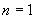 的情况 .
的情况 .
正解:证明:(1)当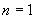 时,左式
时,左式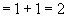 ,右式
,右式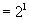 ,所以等式成立.
,所以等式成立.
(2)假设当 (
(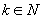 )时,等式成立,
)时,等式成立,
即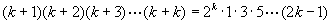 ,
,
那么当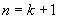 时,
时,
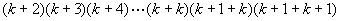
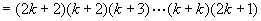
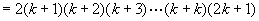
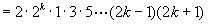
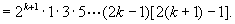
这就是说,当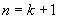 时,等式成立.
时,等式成立.
由(1)、(2),可知等式对任意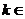 N成立.
N成立.
[例3] 是否存在自然数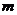 ,使得
,使得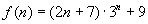 对任意自然数
对任意自然数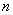 ,都能被
,都能被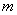 整除,若存在,求出
整除,若存在,求出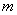 的最大值,并证明你的结论;若不存在,说明理由.
的最大值,并证明你的结论;若不存在,说明理由.
分析 本题是开放性题型,先求出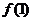 ,
,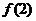 ,
,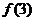 …再归纳、猜想、证明.
…再归纳、猜想、证明.
解: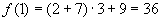 ,
,
 ,
,
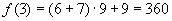 ,
,
……
猜想, 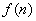 能被36整除,用数学归纳法证明如下:
能被36整除,用数学归纳法证明如下:
(1)当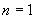 时,
时,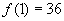 ,能被36整除.
,能被36整除.
(2)假设当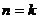 ,(
,(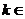 N)时,
N)时,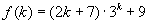 能被36整除.
能被36整除.
那么,当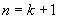 时,
时,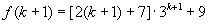
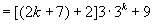
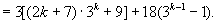
由归纳假设,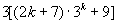 能被36整除,
能被36整除,
当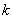 为自然数时,
为自然数时,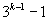 为偶数,则
为偶数,则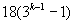 能被36整除.
能被36整除.
∴ 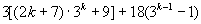 能被36整除,
能被36整除,
这就是说当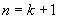 时命题成立.
时命题成立.
由(1)、(2)对任意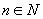 ,
, 都能被36整除.
都能被36整除.
当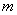 取大于36的自然数时,
取大于36的自然数时,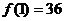 不能被
不能被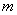 整除,所以36为最大.
整除,所以36为最大.
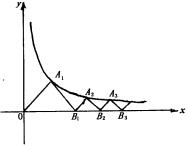
[例4] 设点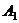 是曲线C:
是曲线C: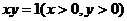 与直线
与直线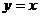 的交点,过
的交点,过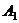 点作直线
点作直线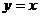 的垂线交
的垂线交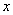 轴于
轴于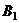 ,过
,过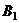 点作直线
点作直线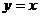 的平行线交曲线C于
的平行线交曲线C于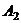 ,再过
,再过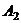 点作
点作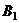
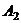 的垂线作交X轴于
的垂线作交X轴于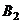 ,如此继续下去可得到一系列的点
,如此继续下去可得到一系列的点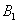 ,
,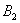 ,…,
,…,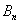 ,…如图,试求
,…如图,试求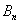 的横坐标
的横坐标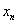 的通项公式.
的通项公式.
分析 本题并没有指明求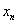 通项公式的方法,可用归纳--猜想--证明的方法,也可以通过寻求
通项公式的方法,可用归纳--猜想--证明的方法,也可以通过寻求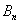 与
与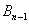 的递推关系式求
的递推关系式求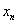 的通项公式.
的通项公式.
解:解法一 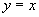 与
与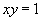 (
(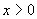 ,
,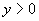 )联立,解得
)联立,解得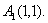
直线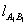 的方程为
的方程为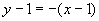 , 令
, 令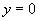 ,得
,得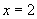 ,所以点
,所以点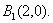
直线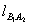 的方程为
的方程为 与
与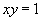 联立,消元得
联立,消元得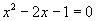 (
(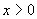 ),解得
),解得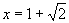 , 所以点
, 所以点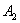 (
(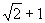 ,
,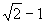 ).
).
直线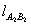 的方程为
的方程为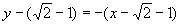 ,
,
令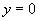 ,得
,得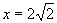 ,所以点
,所以点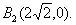 同样可求得点
同样可求得点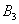 (
(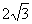 ,0)
,0)
……
由此推测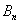 (
(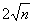 ,0),即
,0),即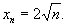
用数学归纳法证明
(1)当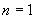 时,由
时,由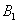 点的坐标为(
点的坐标为(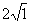 ,0),
,0),
即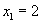 ,所以命题成立.
,所以命题成立.
(2)假设当 时命题成立,
时命题成立,
即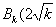 ,0),则当
,0),则当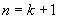 时,
时,
由于直线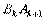 的方程为
的方程为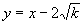 ,
,
把它与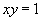 (
(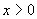 ,
,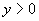 )联立,
)联立,
消去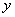 可得
可得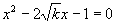 (
(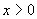 ),
),
∴ 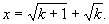
于是 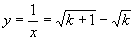
即点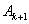 的坐标为(
的坐标为(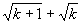 ,
,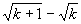 ).
).
∴ 直线 的方程为
的方程为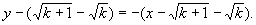
令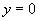 得,
得,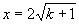
即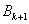 点的坐标为(
点的坐标为(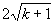 ,0)
,0)
∴ 当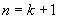 时,命题成立.
时,命题成立.
解法二 设点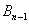 ,
,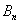 的坐标分别为(
的坐标分别为(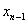 ,0)、(
,0)、(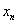 ,0),
,0),
建立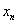 与
与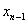 的递推关系
的递推关系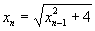 ,即
,即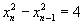 ,
,
由数列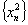 是等差数列,且
是等差数列,且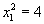 ,公差
,公差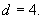
可求得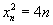 (
(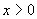 ),
),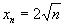 .
.
用数学归纳法证明与自然数n有关的几何命题,由k过渡到k+1常利用几何图形来分析图形前后演变情况.
[例5] 有n个圆,其中每两个圆都相交于两点,并且每三个圆都不相交于同一点,求证:这n个圆把平面分成f(n)=n2-n+2个部分.
证明①当n=1时,即一个圆把平面分成二个部分f(1)=2
又n=1时,n2-n+2=2,∴命题成立
②假设n=k时,命题成立,即k个圆把平面分成f(k)=k2-k+2个
部分,那么设第k+1个圆记⊙O,由题意,它与k个圆中每个圆
交于两点,又无三圆交于同一点,于是它与其它k个圆相交于2k
个点.把⊙O分成2k条弧而每条弧把原区域分成2块,因此这平
面的总区域增加2k块,即f(k+1)=k2-k+2+2k=(k+1)2-(k+1)+2
即n=k+1时命题成立.
由①②可知对任何n∈N命题均成立.
说明: 本题如何应用归纳假设及已知条件,其关键是分析k增加“1”时,研究第k+1个圆与其它k个圆的交点个数问题.
[例6] 已知n≥2,n∈N
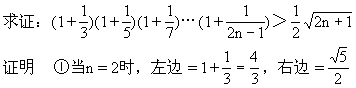
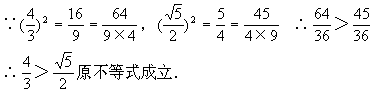
②假设n=k时,原不等式成立.
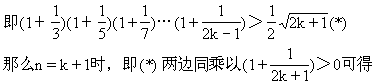
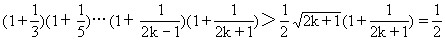
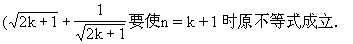
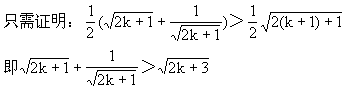
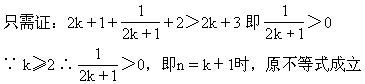
由①②可知,对任何n∈N(n≥2),原不等式均成立.
3. 数学归纳法是一种证明方法,归纳推理是一种推理方法.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com