
6.设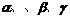 为平面,
为平面,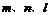 为直线,则
为直线,则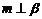 的一个充分条件是
的一个充分条件是
A. 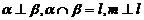 B.
B.
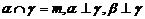
C. 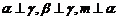 D.
D.
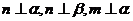
5.已知直线m、n、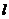 与平面
与平面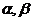 ,给出下列六个命题:
,给出下列六个命题:
①若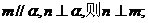 ②若
②若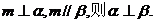
③若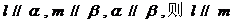
④若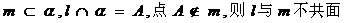
⑤若m 、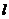 是异面直线,
是异面直线,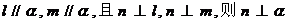 ;
;
⑥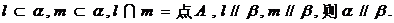 其中假命题有
其中假命题有
A.0 B.1 C.2 D.3
4. 在正四面体P-ABC中,D,E,F分别是AB,BC,CA的中点,下面四个结论中不成立是
A.BC//平面PDF B.DF⊥平面PAE
C.平面PDF⊥平面ABC D.平面PAE⊥平面ABC
3.棱长为 的正方体外接球的表面积为
的正方体外接球的表面积为

2.在空间,下列命题中正确的个数为
①平行于同一直线的两条直线平行;②垂直于同一直线的两条直线平行;
③平行于同一平面的两条直线平行;④垂直于同一平面的两条直线平行;
(A)0 (B)1 (C)2 (D)3
1.从长方体一个顶点出发的三个面的面积分别为6,8,12,则其对角线的长为
(A)3
(B)5 (C) 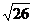 (D)
(D)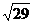
3.突出重点
综合考查在知识与方法的交汇点处设计命题,在不等式问题中蕴含着丰富的函数思想,不等式又为研究函数提供了重要的工具,不等式与函数既是知识的结合点,又是数学知识与数学方法的交汇点,因而在历年高考题中始终是重中之重。在全面考查函数与不等式基础知识的同时,将不等式的重点知识以及其他知识有机结合,进行综合考查,强调知识的综合和知识的内在联系,加大数学思想方法的考查力度,是高考对不等式考查的又一新特点。
2.强化不等式的应用
突出不等式的知识在解决实际问题中的应用价值,借助不等式来考查学生的应用意识。
高考中除单独考查不等式的试题外,常在一些函数、数列、立体几何、解析几何和实际应用问题的试题中涉及不等式的知识,加强不等式应用能力,是提高解综合题能力的关键.因此,在复习时应加强这方面训练,提高应用意识,总结不等式的应用规律,才能提高解决问题的能力。
如在实际问题应用中,主要有构造不等式求解或构造函数求函数的最值等方法,求最值时要注意等号成立的条件,避免不必要的错误。
1.在复习不等式的解法时,加强等价转化思想的训练与复习
解不等式的过程是一个等价转化的过程,通过等价转化可简化不等式(组),以快速、准确求解。
加强分类讨论思想的复习.在解不等式或证不等式的过程中,如含参数等问题,一般要对参数进行分类讨论.复习时,学生要学会分析引起分类讨论的原因,合理的分类,做到不重不漏。
加强函数与方程思想在不等式中的应用训练。不等式、函数、方程三者密不可分,相互联系、互相转化.如求参数的取值范围问题,函数与方程思想是解决这类问题的重要方法.在不等式的证明中,加强化归思想的复习,证不等式的过程是一个把已知条件向要证结论的一个转化过程,既可考查学生的基础知识,又可考查学生分析问题和解决问题的能力,正因为证不等式是高考考查学生代数推理能力的重要素材,复习时应引起我们的足够重视.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com