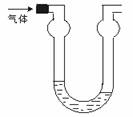
3.(2002年上海理综，20)双球洗气管是一种多用途仪器，常用于去除杂质、气体干燥、气体吸收(能防止倒吸)等实验操作。如右图所示是用水吸收下列某气体时的情形，根据下面附表判断由左方进入的被吸收气体是

A.Cl₂　　　　　　　　　　　　 　　　　　　 B.HCl

C.H₂S　　　　　　　　　　　　 　　　　　　 D.CO₂

附：四种气体的溶解度表(室温下)

2.(2002年上海，17)1998年诺贝尔化学奖授予科恩和波普尔，以表彰他们在理论化学领域做出的重大贡献。他们的工作使实验和理论能够共同协力探讨分子体系的性质，引起整个化学领域正在经历一场革命性的变化。下列说法正确的是

A.化学不再是纯实验科学

B.化学不再需要实验

C.化学不做实验，就什么都不知道

D.未来化学的方向还是经验化

1.(2002年上海，13)以下实验能获得成功的是

A.用含结晶水的醋酸钠和碱石灰共热制甲烷气体

B.将铁屑、溴水、苯混合制溴苯

C.在苯酚溶液中滴入少量稀溴水出现白色沉淀

D.将铜丝在酒精灯上加热后，立即伸入无水乙醇中，铜丝恢复成原来的红色

1.

4.利用函数的连续性求下列极限.

(1)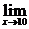(lg²x+3lgx+4)；(2)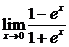，(3)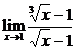

初等函数(比如x^α;α常数，指数函数、对数函数、正弦函数等等)在其定义域里每一点处的极限值等于该点的函数值，因为初等函数在其定义域内是连续的，这样就可以求初等函数的极限了.(1)(2)可以用此法求解，(3)中，由于在x=1处不连续，所以不能直接用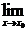f(x)=f(x₀)来求极限，可以设法约去分子、分母的公因式，再求极限.

解：(1)由于lg²x+3lgx+4在x=10处连续.因此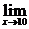(1g²x+3lgx+4)=lg²10+3lg10+4=8.

(2)由于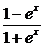在x=0处连续，因此．

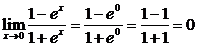(3)由于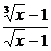在x=1处不连续.

因此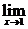

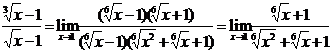
(x=1点为此函数的连续点)

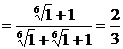
3.已知函数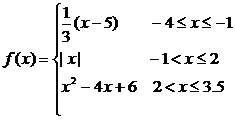

(1)求f(x)的定义域；(2)作出f(x)的图形；(3)判断f(x)是否处处连续.

解：(1)f(x)的定义域是［－4，3.5］.

(2)f(x)的图象如图所示.

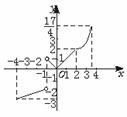
(3)由f(x)的图象可知，在定义域［－4，3.5］上，f(x)在点x=－1处不连续，因为f(x)在x=－1处没有极限.

点评：分段函数的定义域是其各段定义域的并集，易知基本初等函数在其定义域内都是连续的，因此分段函数在其各段内也是连续的，重点应判断各段的交界处是否连续，对这些点应用连续的定义判断，凡其图象在某点处断开，则函数在该点处不连续.

2.利用下列函数的图象，说明函数在给定点处是否连续.

(1)f(x)=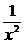，点x=0

解：∵f(x)在x=0处没有定义. ∴f(x)在x=0处不连续.

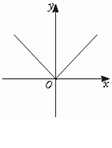(2)f(x)=|x|.点x=0

解：∵f(x)=0=f(0),∴f(x)在x=0处连续.

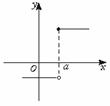
1．下面我们直接从图中，观察函数x=a处是否连续，并说出理由.

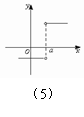
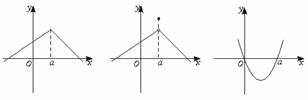
(1)　　　　　　 　　(2)　 　　(3)　　 　　　　　 (4)

(1)连续.因为函数在点x=a处有定义，极限存在，并且极限值等于在a点的函数值.(如图(1))

　(2)不连续.因为函数在x=a处的极限值不等于在x=a处的函数值.(如图(2))

(3)连续.因为函数在点x=a处，有定义，有极限，极限值等于函数值.(如图(3))

(4)不连续.因为函数在x=a处没有极限.(如图(4))

(5)不连续.因为函数在x=a处没有定义.(如图(5))

例1 讨论下列函数在给定点处的连续性.

(1)f(x)=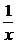，点x=0.　 (2)g(x)=sinx，点x=0.

分析：我们如果要很直观地看在给定点是否连续，画图方法最方便．

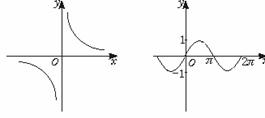
我们已经画出了两个函数的图象了.从图中，我们可以直接看出在x=0处函数连续的情况，

函数f(x)=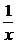在点x=0处不连续，因为函数f(x)=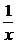在点x=0处没有定义.

函数g(x)=sinx在点x=0处连续，因为函数g(x)=sinx，在x=0及附近都有定义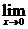，sinx存在且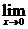sinx=0而sin0=0.

解：(1)∵函数f(x)=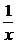在点x=0处没有定义　　 ∴它在点x=0处不连续.

解：(2)∵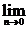sinx=0=sin0，∴函数g(x)=sinx在点x=0处是连续的.

点评：写g(x)=sinx在点x=0处连续只要把第三个条件写一下就可以，因为它已经包含前两个条件了，我们已经知道函数在一点连续的定义了．

例2　 求f(x)=x　 x∈［－1，1］的最大值和最小值．

解：最大值　 f(1)=1；最小值　 f(－1)=－1．

7.最大值最小值定理

如果f(x)是闭区间［a，b］上的连续函数，那么f(x)在闭区间［a，b］上有最大值和最小值

我们现在已经学习了函数在一点连续的定义，和需要满足的三个条件，下面看两个例子，看在给定点处是否连续，都要说明理由的