
3.函数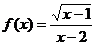 的定义域为
( )
的定义域为
( )
A、[1,2)∪(2,+∞) B、(1,+∞) C、[1,2) D、[1,+∞)
2.设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( )
A、{1,2} B、{1,5} C、{2,5} D、{1,2,5}
1、下列四个集合中,是空集的是( )
A
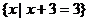 B
B
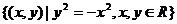
C
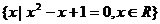 D
D
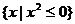
22.(本小题满分12分)
如图,四面体ABCD中,O、E分别是BD、BC的中点,
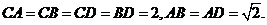
(1)求证: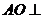 平面BCD;
平面BCD;
(2)求异面直线AB与CD所成角的大小;
(3)求点E到平面ACD的距离。
高三第一轮复习训练题
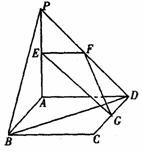
21. 如图,平面PAD⊥平面ABCD,ABCD为正方形,
△PAD是直角三角形,且PA=AD=2,E、F、G分别是
线段PA、PD、CD的中点.
(1)求证:EFG⊥平面PAB;
(2)求异面直线EG与BD所成的角;
|

20.如图,△ABC和△DBC所在平面互相垂直,且AB=BC=BD,∠ABC=∠DBC=120º,求:⑴A、D连线和平面DBC所成的角;⑵二面角A-BD-C的正切值。
19.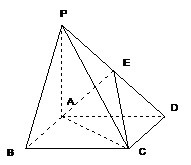 如图,在四棱锥
如图,在四棱锥 中,四边形
中,四边形 为正方形,
为正方形, 点在平面
点在平面 内的射影为
内的射影为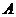 ,且
,且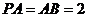 ,
,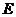 为
为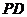 中点.
中点.
(1)证明: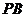 //平面
//平面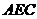 ;
;
(2)证明:平面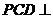 平面
平面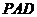 ;
;
(3)求二面角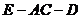 的正切值.
的正切值.

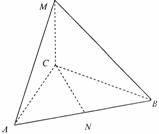
18.在三棱锥M-ABC中,CM⊥平面ABC,MA=MB,NA=NB=NC.
(1)求证:AM⊥BC;
(1)若∠AMB=60°,求直线AM与CN所成的角.
17. 如图,正三棱柱ABC-A1B1C1的各棱长都等于2,D在AC1上,F为BB1中点,且FD⊥AC1。
(1)试求 的值;
的值;
 (2)求二面角F-AC1-C的大小;
(2)求二面角F-AC1-C的大小;
(3)求点C1到平面AFC的距离.
16.给出以下四个命题:
①如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行,
②如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面
③如果两条直线都平行于一个平面,那么这两条直线互相平行,
④如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直.
其中真命题的是 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com