
题型1:正、余弦定理
例1.(1)在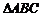 中,已知
中,已知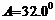 ,
,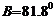 ,
,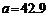 cm,解三角形;
cm,解三角形;
(2)在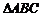 中,已知
中,已知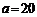 cm,
cm,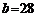 cm,
cm,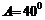 ,解三角形(角度精确到
,解三角形(角度精确到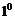 ,边长精确到1cm)。
,边长精确到1cm)。
解析:(1)根据三角形内角和定理,
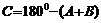
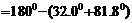
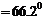 ;
;
根据正弦定理,
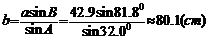 ;
;
根据正弦定理,
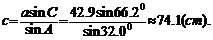
(2)根据正弦定理,
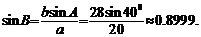
因为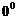 <
<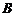 <
<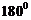 ,所以
,所以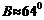 ,或
,或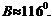
①当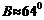 时,
时, 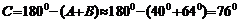 ,
,
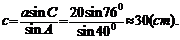
②当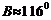 时,
时,
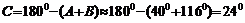 ,
,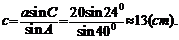
点评:应用正弦定理时(1)应注意已知两边和其中一边的对角解三角形时,可能有两解的情形;(2)对于解三角形中的复杂运算可使用计算器。
例2.(1)在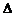 ABC中,已知
ABC中,已知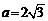 ,
,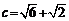 ,
,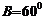 ,求b及A;
,求b及A;
(2)在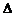 ABC中,已知
ABC中,已知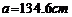 ,
,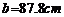 ,
,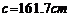 ,解三角形
,解三角形
解析:(1)∵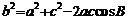
=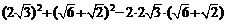 cos
cos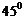
=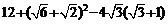
=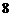
∴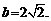
求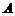 可以利用余弦定理,也可以利用正弦定理:
可以利用余弦定理,也可以利用正弦定理:
解法一:∵cos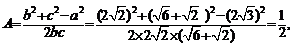 ∴
∴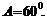
解法二:∵sin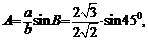
又∵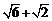 >
>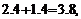
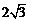 <
<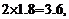 ∴
∴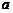 <
<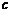 ,即
,即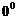 <
<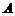 <
<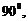
∴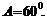
(2)由余弦定理的推论得:
cos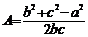
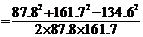
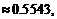
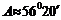 ;
;
cos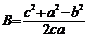
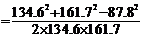
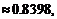
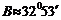 ;
;
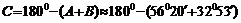
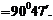
点评:应用余弦定理时解法二应注意确定A的取值范围。
题型2:三角形面积
例3.在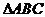 中,
中,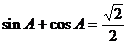 ,
,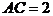 ,
,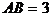 ,求
,求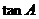 的值和
的值和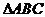 的面积。
的面积。
解法一:先解三角方程,求出角A的值。
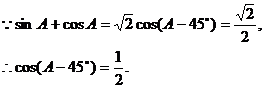
又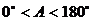 ,
, 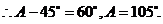
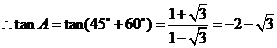 ,
,
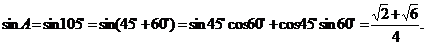
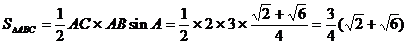 。
。
解法二:由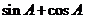 计算它的对偶关系式
计算它的对偶关系式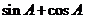 的值。
的值。
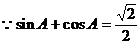 ①
①
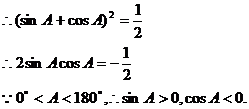
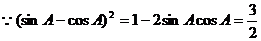 ,
,
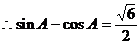 ②
②
① + ② 得 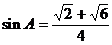 。
。
① - ② 得 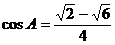 。
。
从而 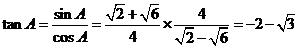 。
。
以下解法略去。
点评:本小题主要考查三角恒等变形、三角形面积公式等基本知识,着重数学考查运算能力,是一道三角的基础试题。两种解法比较起来,你认为哪一种解法比较简单呢?
例4.(06年湖南)已知ΔABC的三个内角A、B.C成等差数列,其外接圆半径为1,且有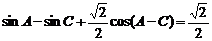 。(1)求A、B.C的大小;(2)求ΔABC的的面积。
。(1)求A、B.C的大小;(2)求ΔABC的的面积。
解析:∵A+B+C=180°且2B=A+C,∴B=60°,A+C=120°,C=120°-A。
∵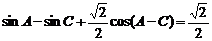 ,
,
∴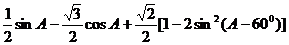 =
=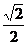 ,
,
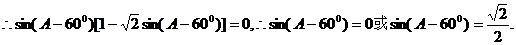 又∵0°<A<180°,∴A=60°或A=105°,
又∵0°<A<180°,∴A=60°或A=105°,
当A=60°时,B=60°,C=60°,
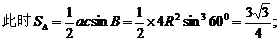
当A=105°时,B=60°,C=15°,
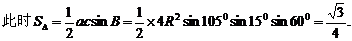
点评:要善于借助三角形内的部分变形条件,同时兼顾三角形的面积公式求得结果。
题型3:与三角形边角相关的问题
例5.(1)(2005江苏5)△ABC中,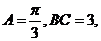 则△ABC的周长为( )
则△ABC的周长为( )
A.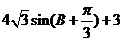 B.
B.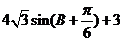
C.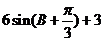 D.
D.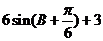
(2)(06年全国2文,17)在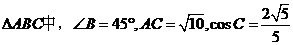 ,求(1)
,求(1)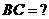 (2)若点
(2)若点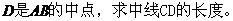
解析:(1)答案:D
解析:在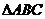 中,由正弦定理得:
中,由正弦定理得: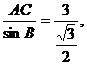 化简得AC=
化简得AC=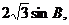
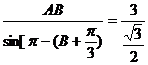 ,化简得AB=
,化简得AB=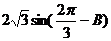 ,
,
所以三角形的周长为:3+AC+AB=3+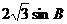 +
+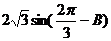
=3+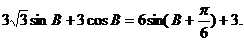 。故选D。
。故选D。
(2)解:(1)由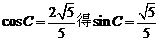 ,
,
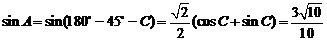 ,
,
由正弦定理知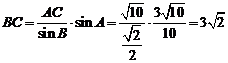 ,
,
(2)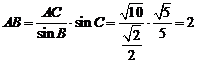 ,
,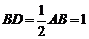 。
。
由余弦定理知:
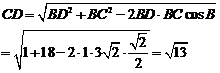
点评:本题考查了在三角形正弦定理的的运用,以及三角公式恒等变形、化简等知识的运用。
例6.在锐角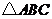 中,角
中,角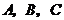 所对的边分别为
所对的边分别为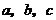 ,已知
,已知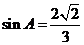 ,(1)求
,(1)求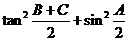 的值;(2)若
的值;(2)若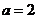 ,
,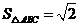 ,求
,求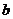 的值。
的值。
解析:(1)因为锐角△ABC中,A+B+C=p,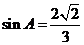 ,所以cosA=
,所以cosA=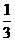 ,
,
则
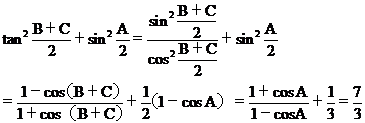
(2)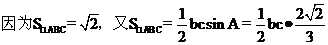 ,则bc=3。
,则bc=3。
将a=2,cosA=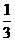 ,c=
,c=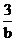 代入余弦定理:
代入余弦定理: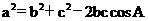 中,
中,
得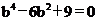 解得b=
解得b=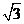 。
。
点评:知道三角形边外的元素如中线长、面积、周长等时,灵活逆用公式求得结果即可。
题型4:三角形中求值问题
例7.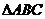 的三个内角为
的三个内角为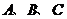 ,求当A为何值时,
,求当A为何值时,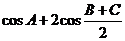 取得最大值,并求出这个最大值。
取得最大值,并求出这个最大值。
解析:由A+B+C=π,得=-,所以有cos =sin。
cosA+2cos =cosA+2sin =1-2sin2 + 2sin=-2(sin - )2+ ;
当sin = ,即A=时, cosA+2cos取得最大值为。
点评:运用三角恒等式简化三角因式最终转化为关于一个角的三角函数的形式,通过三角函数的性质求得结果。
例8.(06四川文,18)已知A、B、C是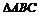 三内角,向量
三内角,向量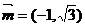
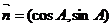 ,且
,且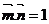 ,(Ⅰ)求角A;(Ⅱ)若
,(Ⅰ)求角A;(Ⅱ)若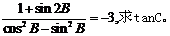
解析:(Ⅰ)∵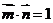 ∴
∴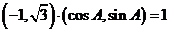 ,即
,即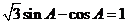 ,
,
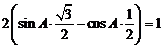 ,
,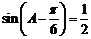 ;
;
∵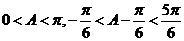 ,∴
,∴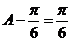 ,∴
,∴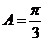 。
。
(Ⅱ)由题知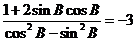 ,
,
整理得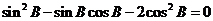 ,∴
,∴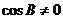 ∴
∴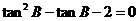 ;
;
∴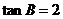 或
或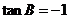 ,而
,而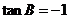 使
使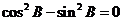 ,舍去;
,舍去;
∴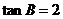 。
。
点评:本小题主要考察三角函数概念、同角三角函数的关系、两角和与差的三角函数的公式以及倍角公式,考察应用、分析和计算能力。
题型5:三角形中的三角恒等变换问题
例9.在△ABC中,a、b、c分别是∠A、∠B、∠C的对边长,已知a、b、c成等比数列,且a2-c2=ac-bc,求∠A的大小及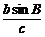 的值。
的值。
分析:因给出的是a、b、c之间的等量关系,要求∠A,需找∠A与三边的关系,故可用余弦定理。由b2=ac可变形为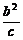 =a,再用正弦定理可求
=a,再用正弦定理可求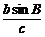 的值。
的值。
解法一:∵a、b、c成等比数列,∴b2=ac。
又a2-c2=ac-bc,∴b2+c2-a2=bc。
在△ABC中,由余弦定理得:cosA=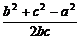 =
=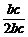 =
=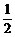 ,∴∠A=60°。
,∴∠A=60°。
在△ABC中,由正弦定理得sinB=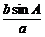 ,∵b2=ac,∠A=60°,
,∵b2=ac,∠A=60°,
∴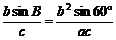 =sin60°=
=sin60°=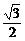 。
。
解法二:在△ABC中,
由面积公式得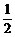 bcsinA=
bcsinA=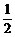 acsinB。
acsinB。
∵b2=ac,∠A=60°,∴bcsinA=b2sinB。
∴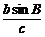 =sinA=
=sinA=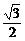 。
。
评述:解三角形时,找三边一角之间的关系常用余弦定理,找两边两角之间的关系常用正弦定理。
例10.(2002京皖春,17)在△ABC中,已知A、B、C成等差数列,求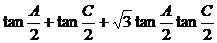 的值。
的值。
解析:因为A、B、C成等差数列,又A+B+C=180°,所以A+C=120°,
从而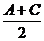 =60°,故tan
=60°,故tan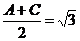 .由两角和的正切公式,
.由两角和的正切公式,
得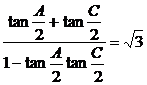 。
。
所以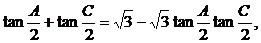
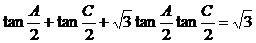 。
。
点评:在三角函数求值问题中的解题思路,一般是运用基本公式,将未知角变换为已知角求解,同时结合三角变换公式的逆用。
题型6:正、余弦定理判断三角形形状
例11.(2002上海春,14)在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是( )
A.等腰直角三角形 B.直角三角形
C.等腰三角形 D.等边三角形
答案:C
解析:2sinAcosB=sin(A+B)+sin(A-B)又∵2sinAcosB=sinC,
∴sin(A-B)=0,∴A=B
点评:本题考查了三角形的基本性质,要求通过观察、分析、判断明确解题思路和变形方向,通畅解题途径。
例12.(06安徽理,11)如果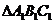 的三个内角的余弦值分别等于
的三个内角的余弦值分别等于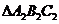 的三个内角的正弦值,则( )
的三个内角的正弦值,则( )
A.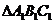 和
和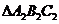 都是锐角三角形
都是锐角三角形
B.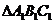 和
和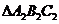 都是钝角三角形
都是钝角三角形
C.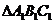 是钝角三角形,
是钝角三角形,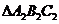 是锐角三角形
是锐角三角形
D.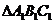 是锐角三角形,
是锐角三角形,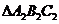 是钝角三角形
是钝角三角形
解析: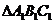 的三个内角的余弦值均大于0,则
的三个内角的余弦值均大于0,则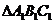 是锐角三角形,
是锐角三角形,
若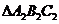 是锐角三角形,由
是锐角三角形,由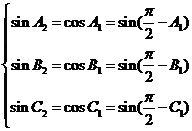 ,得
,得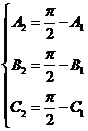 ,
,
那么,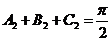 ,所以
,所以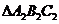 是钝角三角形。故选D。
是钝角三角形。故选D。
点评:解决此类问题时要结合三角形内角和的取值问题,同时注意实施关于三角形内角的一些变形公式。
 题型7:正余弦定理的实际应用
题型7:正余弦定理的实际应用
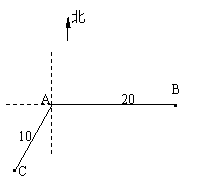
例13.(06上海理,18)如图,当甲船位于A处时获悉,在其正东方向相距20海里的B处有一艘渔船遇险等待营救.甲船立即前往救援,同时把消息告知在甲船的南偏西30 ,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1
,相距10海里C处的乙船,试问乙船应朝北偏东多少度的方向沿直线前往B处救援(角度精确到1 )?
)?
解析:连接BC,由余弦定理得BC2=202+102-2×20×10COS120°=700.
于是,BC=10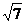 。 ∵
。 ∵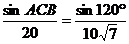 ,∴sin∠ACB=
,∴sin∠ACB=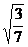 ,
,
∵∠ACB<90°,∴∠ACB=41°。
∴乙船应朝北偏东71°方向沿直线前往B处救援。
点评:解三角形等内容提到高中来学习,又近年加强数形结合思想的考查和对三角变换要求的降低,对三角的综合考查将向三角形中问题伸展,但也不可太难,只要掌握基本知识、概念,深刻理解其中基本的数量关系即可过关。
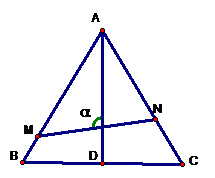 例14.(06江西理,19)如图,已知△ABC是边长为1的正三角形,M、N分别是
例14.(06江西理,19)如图,已知△ABC是边长为1的正三角形,M、N分别是
边AB、AC上的点,线段MN经过△ABC的中心G,设ÐMGA=a(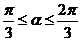 )
)
(1)试将△AGM、△AGN的面积(分别记为S1与S2);
(2)表示为a的函数,求y=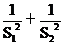 的最大值与最小值。
的最大值与最小值。
解析:(1)因为G是边长为1的正三角形ABC的中心,所以 AG=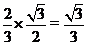 ,ÐMAG=
,ÐMAG=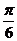 ,由正弦定理
,由正弦定理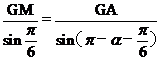 得
得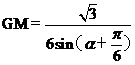 ,则S1=
,则S1=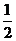 GM·GA·sina=
GM·GA·sina=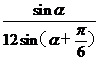 。同理可求得S2=
。同理可求得S2=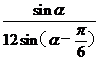 。
。
(2)y=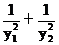 =
=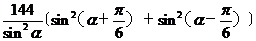 =72(3+cot2a)因为
=72(3+cot2a)因为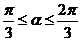 ,
,
所以当a=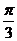 或a=
或a=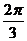 时,y取得最大值ymax=240,当a=
时,y取得最大值ymax=240,当a=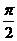 时,y取得最小值ymin=216。
时,y取得最小值ymin=216。
点评:三角函数有着广泛的应用,本题就是一个典型的范例。通过引入角度,将图形的语言转化为三角的符号语言,再通过局部的换元,又将问题转化为我们熟知的函数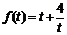 ,这些解题思维的拐点,你能否很快的想到呢?
,这些解题思维的拐点,你能否很快的想到呢?
5.三角形中的三角变换
三角形中的三角变换,除了应用上述公式和上述变换方法外,还要注意三角形自身的特点。
(1)角的变换
因为在△ABC中,A+B+C=π,所以sin(A+B)=sinC;cos(A+B)=-cosC;tan(A+B)=-tanC。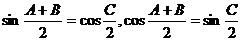 ;
;
(2)三角形边、角关系定理及面积公式,正弦定理,余弦定理。
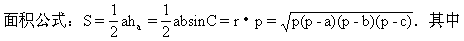
r为三角形内切圆半径,p为周长之半。
(3)在△ABC中,熟记并会证明:∠A,∠B,∠C成等差数列的充分必要条件是∠B=60°;△ABC是正三角形的充分必要条件是∠A,∠B,∠C成等差数列且a,b,c成等比数列。
4.解三角形:由三角形的六个元素(即三条边和三个内角)中的三个元素(其中至少有一个是边)求其他未知元素的问题叫做解三角形.广义地,这里所说的元素还可以包括三角形的高、中线、角平分线以及内切圆半径、外接圆半径、面积等等.解三角形的问题一般可分为下面两种情形:若给出的三角形是直角三角形,则称为解直角三角形;若给出的三角形是斜三角形,则称为解斜三角形。
解斜三角形的主要依据是:
设△ABC的三边为a、b、c,对应的三个角为A、B、C。
(1)角与角关系:A+B+C = π;
(2)边与边关系:a + b > c,b + c > a,c + a > b,a-b < c,b-c < a,c-a > b;
(3)边与角关系:
正弦定理 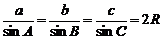 (R为外接圆半径);
(R为外接圆半径);
余弦定理 c2 = a2+b2-2bccosC,b2 = a2+c2-2accosB,a2 = b2+c2-2bccosA;
它们的变形形式有:a = 2R
sinA,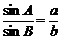 ,
,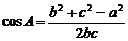 。
。
3.三角形的面积公式:
(1)△=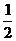 aha=
aha=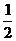 bhb=
bhb=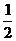 chc(ha、hb、hc分别表示a、b、c上的高);
chc(ha、hb、hc分别表示a、b、c上的高);
(2)△=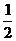 absinC=
absinC=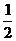 bcsinA=
bcsinA=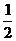 acsinB;
acsinB;
(3)△=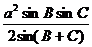 =
=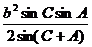 =
=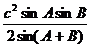 ;
;
(4)△=2R2sinAsinBsinC。(R为外接圆半径)
(5)△=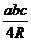 ;
;
(6)△=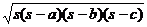 ;
;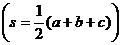 ;
;
(7)△=r·s。
2.斜三角形中各元素间的关系:
如图6-29,在△ABC中,A、B、C为其内角,a、b、c分别表示A、B、C的对边。
(1)三角形内角和:A+B+C=π。
(2)正弦定理:在一个三角形中,各边和它所对角的正弦的比相等。
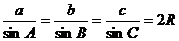 。
。
(R为外接圆半径)
(3)余弦定理:三角形任何一边的平方等于其他两边平方的和减去这两边与它们夹角的余弦的积的两倍。
a2=b2+c2-2bccosA;b2=c2+a2-2cacosB;c2=a2+b2-2abcosC。
1.直角三角形中各元素间的关系:
如图,在△ABC中,C=90°,AB=c,AC=b,BC=a。
(1)三边之间的关系:a2+b2=c2。(勾股定理)
(2)锐角之间的关系:A+B=90°;
(3)边角之间的关系:(锐角三角函数定义)
sinA=cosB=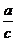 ,cosA=sinB=
,cosA=sinB=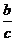 ,tanA=
,tanA=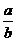 。
。
对本讲内容的考察主要涉及三角形的边角转化、三角形形状的判断、三角形内三角函数的求值以及三角恒等式的证明问题,立体几何体的空间角以及解析几何中的有关角等问题。今后高考的命题会以正弦定理、余弦定理为知识框架,以三角形为主要依托,结合实际应用问题考察正弦定理、余弦定理及应用。题型一般为选择题、填空题,也可能是中、难度的解答题。
(1)通过对任意三角形边长和角度关系的探索,掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题;
(2)能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题。
5.突出向量与其它数学知识的交汇
“新课程增加了新的现代数学内容,其意义不仅在于数学内容的更新,更重要的是引入新的思维方法,可以更有效地处理和解决数学问题和实际应用问题”。因此,新课程卷中有些问题属于新教材与旧教材的结合部,凡涉及此类问题,高考命题都采用了新旧结合,以新带旧或以新方法解决的方法进行处理,从中启示我们在高考学习中,应突出向量的工具性,注重向量与其它知识的交汇与融合,但不宜“深挖洞”。我们可以预测近两年向量高考题的难度不会也不应该上升到压轴题的水平。
4.注重数学思想方法的教学
①.数形结合的思想方法。
由于向量本身具有代数形式和几何形式双重身份,所以在向量知识的整个学习过程中,都体现了数形结合的思想方法,在解决问题过程中要形成见数思形、以形助数的思维习惯,以加深理解知识要点,增强应用意识。
②.化归转化的思想方法。
向量的夹角、平行、垂直等关系的研究均可化归为对应向量或向量坐标的运算问题;三角形形状的判定可化归为相应向量的数量积问题;向量的数量积公式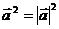 ,沟通了向量与实数间的转化关系;一些实际问题也可以运用向量知识去解决。
,沟通了向量与实数间的转化关系;一些实际问题也可以运用向量知识去解决。
③.分类讨论的思想方法。
如向量可分为共线向量与不共线向量;平行向量(共线向量)可分为同向向量和反向向量;向量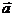 在
在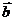 方向上的投影随着它们之间的夹角的不同,有正数、负数和零三种情形;定比分点公式中的
方向上的投影随着它们之间的夹角的不同,有正数、负数和零三种情形;定比分点公式中的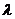 随分点P的位置不同,可以大于零,也可以小于零。
随分点P的位置不同,可以大于零,也可以小于零。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com