
2.考生应立足基础知识和基本方法的复习,以课本题目为主,以熟练技能,巩固概念为目标。
1.本讲内容在高考中以填空题和解答题为主
主要考查:
(1)函数的极限;
(2)导数在研究函数的性质及在解决实际问题中的应用;
(3)计算曲边图形的面积和旋转体的体积。
6.定积分
(1)概念
设函数f(x)在区间[a,b]上连续,用分点a=x0<x1<…<xi-1<xi<…xn=b把区间[a,b]等分成n个小区间,在每个小区间[xi-1,xi]上取任一点ξi(i=1,2,…n)作和式In=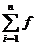 (ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分,记作:
(ξi)△x(其中△x为小区间长度),把n→∞即△x→0时,和式In的极限叫做函数f(x)在区间[a,b]上的定积分,记作: ,即
,即 =
=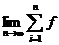 (ξi)△x。
(ξi)△x。
这里,a与b分别叫做积分下限与积分上限,区间[a,b]叫做积分区间,函数f(x)叫做被积函数,x叫做积分变量,f(x)dx叫做被积式。
基本的积分公式: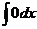 =C;
=C;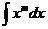 =
=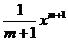 +C(m∈Q, m≠-1);
+C(m∈Q, m≠-1);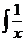 dx=ln
dx=ln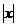 +C;
+C;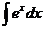 =
=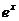 +C;
+C; =
=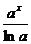 +C;
+C; =sinx+C;
=sinx+C;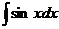 =-cosx+C(表中C均为常数)。
=-cosx+C(表中C均为常数)。
(2)定积分的性质
①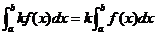 (k为常数);
(k为常数);
②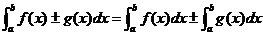 ;
;
 ③
③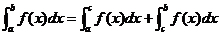 (其中a<c<b
(其中a<c<b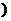 。
。
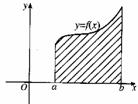
(3)定积分求曲边梯形面积
由三条直线x=a,x=b(a<b),x轴及一条曲线y=f(x)(f(x)≥0)围成的曲边梯的面积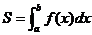 。
。
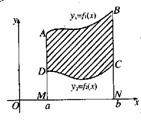 如果图形由曲线y1=f1(x),y2=f2(x)(不妨设f1(x)≥f2(x)≥0),及直线x=a,x=b(a<b)围成,那么所求图形的面积S=S曲边梯形AMNB-S曲边梯形DMNC=
如果图形由曲线y1=f1(x),y2=f2(x)(不妨设f1(x)≥f2(x)≥0),及直线x=a,x=b(a<b)围成,那么所求图形的面积S=S曲边梯形AMNB-S曲边梯形DMNC=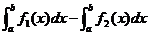 。
。
5.导数的应用
(1)一般地,设函数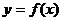 在某个区间可导,如果
在某个区间可导,如果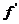
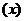
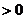 ,则
,则 为增函数;如果
为增函数;如果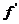
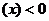 ,则
,则 为减函数;如果在某区间内恒有
为减函数;如果在某区间内恒有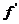
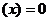 ,则
,则 为常数;
为常数;
(2)曲线在极值点处切线的斜率为0,极值点处的导数为0;曲线在极大值点左侧切线的斜率为正,右侧为负;曲线在极小值点左侧切线的斜率为负,右侧为正;
(3)一般地,在区间[a,b]上连续的函数f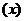 在[a,b]上必有最大值与最小值。①求函数ƒ
在[a,b]上必有最大值与最小值。①求函数ƒ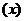 在(a,b)内的极值; ②求函数ƒ
在(a,b)内的极值; ②求函数ƒ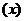 在区间端点的值ƒ(a)、ƒ(b); ③将函数ƒ
在区间端点的值ƒ(a)、ƒ(b); ③将函数ƒ 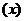 的各极值与ƒ(a)、ƒ(b)比较,其中最大的是最大值,其中最小的是最小值。
的各极值与ƒ(a)、ƒ(b)比较,其中最大的是最大值,其中最小的是最小值。
4.两个函数的和、差、积的求导法则
法则1:两个函数的和(或差)的导数,等于这两个函数的导数的和(或差),
即: (
法则2:两个函数的积的导数,等于第一个函数的导数乘以第二个函数,加上第一个
函数乘以第二个函数的导数,即: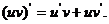
若C为常数,则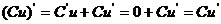 .即常数与函数的积的导数等于常数乘以函数的导数:
.即常数与函数的积的导数等于常数乘以函数的导数: 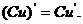
法则3两个函数的商的导数,等于分子的导数与分母的积,减去分母的导数与分子的积,再除以分母的平方: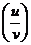 ‘=
‘= (v
(v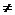 0)。
0)。
形如y=f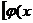
 的函数称为复合函数。复合函数求导步骤:分解--求导--回代。法则:y'|
的函数称为复合函数。复合函数求导步骤:分解--求导--回代。法则:y'|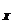 = y'|
= y'|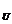 ·u'|
·u'|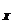
3.常见函数的导出公式.
(1) (C为常数) (2)
(C为常数) (2)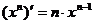
(3) (4)
(4)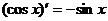
2.导数的几何意义
函数y=f(x)在点x 处的导数的几何意义是曲线y=f(x)在点p(x
处的导数的几何意义是曲线y=f(x)在点p(x ,f(x
,f(x )) 处的切线的斜率。也就是说,曲线y=f(x)在点p(x
)) 处的切线的斜率。也就是说,曲线y=f(x)在点p(x ,f(x
,f(x ))处的切线的斜率是f’(x
))处的切线的斜率是f’(x )。相应地,切线方程为y-y
)。相应地,切线方程为y-y =f/(x
=f/(x )(x-x
)(x-x )。
)。
1.导数的概念
函数y=f(x),如果自变量x在x 处有增量
处有增量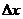 ,那么函数y相应地有增量
,那么函数y相应地有增量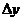 =f(x
=f(x +
+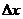 )-f(x
)-f(x ),比值
),比值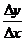 叫做函数y=f(x)在x
叫做函数y=f(x)在x 到x
到x +
+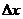 之间的平均变化率,即
之间的平均变化率,即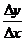 =
=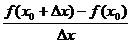 。
。
如果当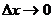 时,
时,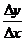 有极限,我们就说函数y=f(x)在点x
有极限,我们就说函数y=f(x)在点x 处可导,并把这个极限叫做f(x)在点x
处可导,并把这个极限叫做f(x)在点x 处的导数,记作f’(x
处的导数,记作f’(x )或y’|
)或y’|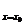 。
。
即f(x )=
)=
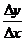 =
=
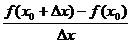 。
。
说明:
(1)函数f(x)在点x 处可导,是指
处可导,是指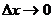 时,
时,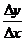 有极限。如果
有极限。如果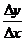 不存在极限,就说函数在点x
不存在极限,就说函数在点x 处不可导,或说无导数。
处不可导,或说无导数。
(2)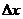 是自变量x在x
是自变量x在x 处的改变量,
处的改变量, 时,而
时,而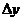 是函数值的改变量,可以是零。
是函数值的改变量,可以是零。
由导数的定义可知,求函数y=f(x)在点x 处的导数的步骤(可由学生来归纳):
处的导数的步骤(可由学生来归纳):
(1)求函数的增量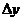 =f(x
=f(x +
+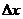 )-f(x
)-f(x );
);
(2)求平均变化率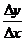 =
=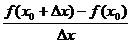 ;
;
(3)取极限,得导数f’(x )=
)=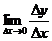 。
。
导数是高中数学中重要的内容,是解决实际问题的强有力的数学工具,运用导数的有关知识,研究函数的性质:单调性、极值和最值是高考的热点问题。在高考中考察形式多种多样,以选择题、填空题等主观题目的形式考察基本概念、运算及导数的应用,也经常以解答题形式和其它数学知识结合起来,综合考察利用导数研究函数的单调性、极值、最值,估计2007年高考继续以上面的几种形式考察不会有大的变化:
(1)考查形式为:选择题、填空题、解答题各种题型都会考察,选择题、填空题一般难度不大,属于高考题中的中低档题,解答题有一定难度,一般与函数及解析几何结合,属于高考的中低档题;
(2)07年高考可能涉及导数综合题,以导数为数学工具考察:导数的物理意义及几何意义,复合函数、数列、不等式等知识。
定积分是新课标教材新增的内容,主要包括定积分的概念、微积分基本定理、定积分的简单应用,由于定积分在实际问题中非常广泛,因而07年的高考预测会在这方面考察,预测07年高考呈现以下几个特点:
(1)新课标第1年考察,难度不会很大,注意基本概念、基本性质、基本公式的考察及简单的应用;高考中本讲的题目一般为选择题、填空题,考查定积分的基本概念及简单运算,属于中低档题;
(2)定积分的应用主要是计算面积,诸如计算曲边梯形的面积、变速直线运动等实际问题要很好的转化为数学模型。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com