
16.某公司租赁甲、乙两种设备生产A,B两类产品,甲种设备每天能生产A类产品5件和B类产品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为__________元.
[解析]:设甲种设备需要生产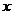 天, 乙种设备需要生产
天, 乙种设备需要生产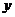 天, 该公司所需租赁费为
天, 该公司所需租赁费为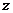 元,则
元,则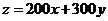 ,甲、乙两种设备生产A,B两类产品的情况为下表所示:
,甲、乙两种设备生产A,B两类产品的情况为下表所示: 

 产品 产品 设备 |
A类产品 (件)(≥50) |
B类产品 (件)(≥140) |
租赁费 (元) |
|
甲设备 |
5 |
10 |
200 |
|
乙设备 |
6 |
20 |
300 |
则满足的关系为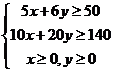 即:
即: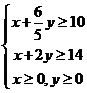 ,
,
作出不等式表示的平面区域,当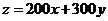 对应的直线过两直线
对应的直线过两直线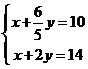 的交点(4,5)时,目标函数
的交点(4,5)时,目标函数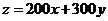 取得最低为2300元.
取得最低为2300元.
答案:2300
[命题立意]:本题是线性规划的实际应用问题,需要通过审题理解题意,找出各量之间的关系,最好是列成表格,找出线性约束条件,写出所研究的目标函数,通过数形结合解答问题..
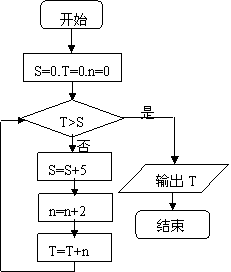
15.执行右边的程序框图,输出的T=
. 

[解析]:按照程序框图依次执行为S=5,n=2,T=2;
S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;
S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30
答案:30
[命题立意]:本题主要考查了循环结构的程序框图,一般都可以
反复的进行运算直到满足条件结束,本题中涉及到三个变量,
注意每个变量的运行结果和执行情况.
14.若函数f(x)=a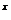 -x-a(a>0且a
-x-a(a>0且a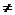 1)有两个零点,则实数a的取值范围是 .
1)有两个零点,则实数a的取值范围是 . 

[解析]: 设函数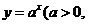 且
且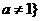 和函数
和函数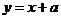 ,则函数f(x)=a
,则函数f(x)=a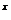 -x-a(a>0且a
-x-a(a>0且a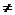 1)有两个零点, 就是函数
1)有两个零点, 就是函数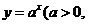 且
且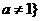 与函数
与函数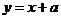 有两个交点,由图象可知当
有两个交点,由图象可知当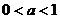 时两函数只有一个交点,不符合,当
时两函数只有一个交点,不符合,当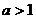 时,因为函数
时,因为函数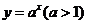 的图象过点(0,1),而直线
的图象过点(0,1),而直线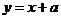 所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是
所过的点(0,a)一定在点(0,1)的上方,所以一定有两个交点.所以实数a的取值范围是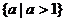 .
. 

答案: 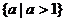
 [命题立意]:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答.
[命题立意]:本题考查了指数函数的图象与直线的位置关系,隐含着对指数函数的性质的考查,根据其底数的不同取值范围而分别画出函数的图象进行解答.
13.在等差数列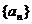 中,
中,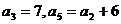 ,则
,则 .
.
[解析]:设等差数列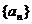 的公差为
的公差为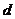 ,则由已知得
,则由已知得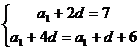 解得
解得 ,所以
,所以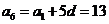 .
. 

答案:13.
[命题立意]:本题考查等差数列的通项公式以及基本计算.
12. 已知定义在R上的奇函数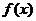 ,满足
,满足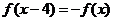 ,且在区间[0,2]上是增函数,则( ).
,且在区间[0,2]上是增函数,则( ). 

A.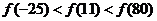 B.
B. 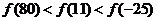
C.  D.
D.
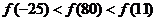
[解析]:因为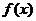 满足
满足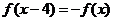 ,所以
,所以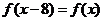 ,所以函数是以8为周期的周期函数, 则
,所以函数是以8为周期的周期函数, 则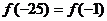 ,
,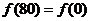 ,
, ,又因为
,又因为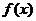 在R上是奇函数,
在R上是奇函数, 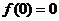 ,得
,得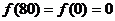 ,
,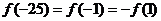 ,而由
,而由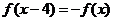 得
得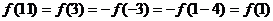 ,又因为
,又因为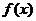 在区间[0,2]上是增函数,所以
在区间[0,2]上是增函数,所以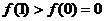 ,所以
,所以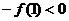 ,即
,即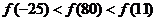 ,故选D.
,故选D. 

答案:D.
[命题立意]:本题综合考查了函数的奇偶性、单调性、周期性等性质,运用化归的数学思想和数形结合的思想解答问题.
第 卷
卷
11.在区间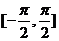 上随机取一个数x,
上随机取一个数x,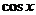 的值介于0到
的值介于0到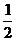 之间的概率为(
).
之间的概率为(
).
A.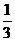 B.
B. C.
C.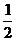 D.
D.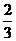


[解析]:在区间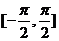 上随机取一个数x,即
上随机取一个数x,即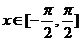 时,要使
时,要使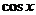 的值介于0到
的值介于0到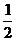 之间,需使
之间,需使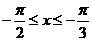 或
或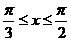 ,区间长度为
,区间长度为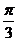 ,由几何概型知
,由几何概型知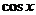 的值介于0到
的值介于0到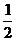 之间的概率为
之间的概率为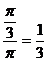 .故选A.
.故选A. 

答案:A
[命题立意]:本题考查了三角函数的值域和几何概型问题,由自变量x的取值范围,得到函数值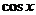 的范围,再由长度型几何概型求得.
的范围,再由长度型几何概型求得.
10. 设斜率为2的直线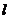 过抛物线
过抛物线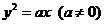 的焦点F,且和
的焦点F,且和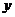 轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).
轴交于点A,若△OAF(O为坐标原点)的面积为4,则抛物线方程为( ).


A.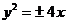 B.
B.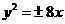 C.
C. 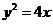 D.
D. 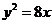
[解析]: 抛物线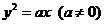 的焦点F坐标为
的焦点F坐标为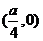 ,则直线
,则直线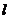 的方程为
的方程为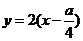 ,它与
,它与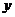 轴的交点为A
轴的交点为A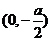 ,所以△OAF的面积为
,所以△OAF的面积为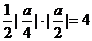 ,解得
,解得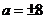 .所以抛物线方程为
.所以抛物线方程为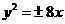 ,故选B.
,故选B. 

答案:B.
[命题立意]:本题考查了抛物线的标准方程和焦点坐标以及直线的点斜式方程和三角形面积的计算.考查数形结合的数学思想,其中还隐含着分类讨论的思想,因参数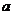 的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
的符号不定而引发的抛物线开口方向的不定以及焦点位置的相应变化有两种情况,这里加绝对值号可以做到合二为一.
9. 已知α,β表示两个不同的平面,m为平面α内的一条直线,则“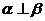 ”是“
”是“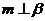 ”的(
)
”的(
)
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件 

[解析]:由平面与平面垂直的判定定理知如果m为平面α内的一条直线,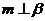 ,则
,则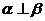 ,反过来则不一定.所以“
,反过来则不一定.所以“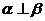 ”是“
”是“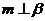 ”的必要不充分条件
”的必要不充分条件 
 .
.
答案:B.
[命题立意]:本题主要考查了立体几何中垂直关系的判定和充分必要条件的概念.
8. 设P是△ABC所在平面内的一点,
设P是△ABC所在平面内的一点,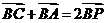 ,则( )
,则( )
A.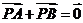 B.
B. 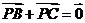 C.
C. 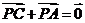 D.
D.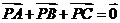
[解析]:因为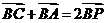 ,所以点P为线段AC的中点,所以应该选B。
,所以点P为线段AC的中点,所以应该选B。
答案:B.
[命题立意]:本题考查了向量的加法运算和平行四边形法则, 

可以借助图形解答。
7. 定义在R上的函数f(x)满足f(x)= 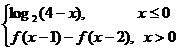 ,则f(3)的值为( )
,则f(3)的值为( )
A.-1 B. -2 C.1 D. 2
[解析]:由已知得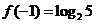 ,
,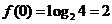 ,
,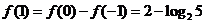 ,
,
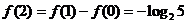 ,
, ,故选B.
,故选B.
答案:B. 

[命题立意]:本题考查对数函数的运算以及推理过程..
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com