
11. 在?ABCD中,A(1,1),
在?ABCD中,A(1,1),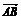 =(6,0),点M是线段AB的中点,线段CM与BD交于点P.
=(6,0),点M是线段AB的中点,线段CM与BD交于点P.
(1)若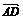 =(3,5),求点C的坐标;
=(3,5),求点C的坐标;
(2)当|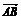 |=|
|=|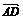 |时,求点P的轨迹.
|时,求点P的轨迹.
解 (1)设点C坐标为(x0,y0),
又 =
=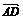 +
+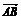 =(3,5)+(6,0)=(9,5),
=(3,5)+(6,0)=(9,5),
即(x0-1,y0-1)=(9,5),
∴x0=10,y0=6,即点C(10,6).
(2)由三角形相似,不难得出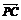 =2
=2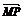
设P(x,y),则
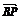 =
=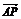 -
-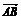 =(x-1,y-1)-(6,0)=(x-7,y-1),
=(x-1,y-1)-(6,0)=(x-7,y-1),
 =
= +
+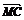 =
=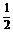
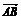 +3
+3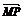

=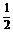
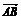 +3(
+3(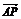 -
-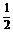
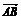 )
)
=3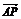 -
-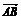 =(3(x-1),3(y-1))-(6,0)
=(3(x-1),3(y-1))-(6,0)
=(3x-9,3y-3),
 ∵|
∵|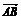 |=|
|=|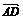 |,∴?ABCD为菱形,
|,∴?ABCD为菱形,
∴AC⊥BD,
∴ ⊥
⊥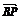 ,即(x-7,y-1)·(3x-9,3y-3)=0.
,即(x-7,y-1)·(3x-9,3y-3)=0.
(x-7)(3x-9)+(y-1)(3y-3)=0,
∴x2+y2-10x-2y+22=0(y≠1).
∴(x-5)2+(y-1)2=4(y≠1).
故点P的轨迹是以(5,1)为圆心,2为半径的圆去掉与直线y=1的两个交点.
10.若a,b为非零向量且a∥b, 1,
1, 2∈R,且
2∈R,且 1
1 2≠0.
2≠0.
求证: 1a+
1a+ 2b与
2b与 1a-
1a- 2b为共线向量.
2b为共线向量.
证明 设a=(x1,y1),b=(x2,y2).
∵a∥b,b≠0,a≠0,∴存在实数m,使得a=mb,
即a=(x1,y1)=(mx2,my2),
∴ 1a+
1a+ 2b=((m
2b=((m 1+
1+ 2)x2,(m
2)x2,(m 1+
1+ 2)y2)
2)y2)
=(m 1+
1+ 2)(x2,y2)
2)(x2,y2)
同理 1a-
1a- 2b=(m
2b=(m 1-
1- 2)(x2,y2),
2)(x2,y2),
∴( 1a+
1a+ 2b)∥(
2b)∥( 1a-
1a- 2b)∥b,
2b)∥b,
而b≠0,∴( 1a+
1a+ 2b)∥(
2b)∥( 1a-
1a- 2b).
2b).
9.已知A(-2,4),B(3,-1),C(-3,-4).
设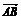 =a,
=a,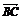 =b,
=b, =c,且
=c,且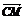 =3c,
=3c, =-2b,
=-2b,
(1)求:3a+b-3c;
(2)求满足a=mb+nc的实数m,n.
解 由已知得a=(5,-5),b=(-6,-3),c=(1,8).
(1)3a+b-3c=3(5,-5)+(-6,-3)-3(1,8)
=(15-6-3,-15-3-24)=(6,-42).
(2)∵mb+nc=(-6m+n,-3m+8n),
∴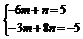 ,解得
,解得 .
.
8.(2008·菏泽模拟)已知向量m=(a-2,-2),n=(-2,b-2),m∥n (a>0,b>0),则ab的最小值是 .
答案 16
7.(2008·全国Ⅱ文)设向量a=(1,2),b=(2,3),若向量 a+b与向量c=(-4,-7)共线,则
a+b与向量c=(-4,-7)共线,则 = .
= .
答案 2
6.设0≤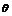 <2
<2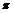 ,已知两个向量
,已知两个向量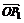 =(cos
=(cos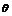 ,sin
,sin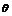 ),
),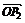 =(2+sin
=(2+sin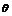 ,2-cos
,2-cos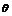 ),则向量
),则向量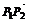 长度的最大值是
.
长度的最大值是
.
答案 3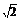
5.(2008·辽宁文)已知四边形ABCD的顶点A(0,2)、B(-1,-2)、C(3,1),且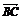 =2
=2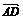 ,则顶点D的坐标为 .
,则顶点D的坐标为 .
答案 
4.(2007·北京文)已知向量a=(2,4),b=(1,1),若向量b⊥(a+ b),则实数
b),则实数 的值是 .
的值是 .
答案 -3
3.已知向量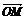 =(3,-2),
=(3,-2),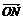 =(-5,-1),则
=(-5,-1),则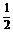
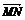 =
.
=
.
答案 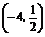
2.设a、b是不共线的两个非零向量,已知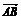 =2a+pb,
=2a+pb,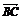 =a+b,
=a+b,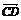 =a-2b.若A、B、D三点共线,则
=a-2b.若A、B、D三点共线,则
p的值为 .
答案 -1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com