
3.下列命题中不正确的命题个数是 ( )
①若A、B、C、D是空间任意四点,则有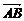 +
+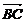 +
+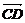 +
+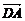 =0;
=0;
②|a|-|b|=|a+b|是a、b共线的充要条件;
③若a、b共线,则a与b所在直线平行;
④对空间任意点O与不共线的三点A、B、C,若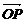 =x
=x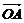 +y
+y +z
+z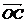 (其中x、y、z∈R),
(其中x、y、z∈R),
则P、A、B、C四点共面 ( C )
A.1 B.2 C.3 D.4
2.设O,P,A,B为空间任意四个点,如果满足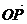 =m
=m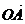 +n
+n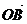 ,且m+n=1,则 ( A )
,且m+n=1,则 ( A )
A.P在直线AB上 B.P不在直线AB上
C.P有可能在直线AB上 D.以上都不对
1.在以下命题中:
①若a、b共线,则a与b所在直线平行
②若a,b所在直线是异面直线,则a与b一定不共面
③若a,b,c三向量两两共面,则a,b,c三向量一定也共面
④若a,b,c三向量共面,则由a,b所在直线所确定的平面与由b,c所在直线所确定的平面一定平行。正确命题的个数为 ( A )
A.0 B.1 C.2 D.3
|
|
内容 |
要求 |
||
|
A |
B |
C |
||
|
1 |
平面及其基本性质 |
|
√ |
|
|
2 |
几何体的直观图 |
√ |
|
|
|
3 |
直线和平面平行的判定与性质 |
|
√ |
|
|
4 |
直线和平面垂直的判定 |
|
√ |
|
|
5 |
三垂线定理及其逆定理 |
|
√ |
|
|
6 |
空间向量的概念及空间向量的加法、减法和数乘 |
|
√ |
|
|
7 |
空间向量的坐标运算 |
|
√ |
|
|
8 |
空间向量的数量积的概念、性质 |
|
√ |
|
|
9 |
用直角坐标计算空间向量的数量积的公式 |
|
√ |
|
|
10 |
空间两点间距离公式 |
|
√ |
|
|
11 |
直线的方向向量、平面的法向量、向量在平面内的射影 |
|
√ |
|
|
12 |
直线和直线、直线和平面、平面和平面所成的角 |
|
√ |
|
|
13 |
距离(对异面直线的距离,只要求会计算给出公垂线或在坐标表示下的距离) |
|
√ |
|
|
14 |
直线和平面垂直的性质 |
|
√ |
|
|
15 |
两个平面平行、垂直的判定与性质 |
|
√ |
|
2.用分数指数幂表示下列各式(a>0,x>0)
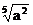
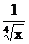
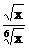
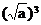
(II)讲授新课
例1.计算下列各式(式中字母都是正数)
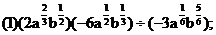
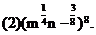
分析:(1)题可以仿照单项式乘除法进行,首先是系数相乘除,然后是同底数幂相乘除,并且要注意符号。(2)题先按积的乘方计算,后按幂的乘方计算,等熟练后可简化计算步骤。对于计算的结果不强求统一用什么形式来表示,没有特别要求,就用分数指数幂的形式表示。如果有特殊要求,可根据要求给出结果,但:
① 结果不能同时含有根式和分数指数;②不能同时含有分母和负指数;
③ 根式需化成最简根式。
解: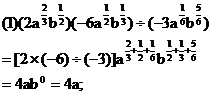
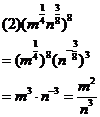 |
例2.计算下列各式:
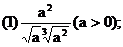
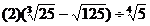
分析:(1)题把根式化成分数指数幂的形式,再计算。
(2)题先把根式化成分数指数幂的最简形式,然后计算。
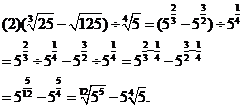 解: 解: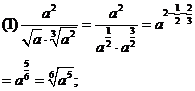 |
例3.求值:
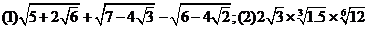
分析:(1)题需把各项被开方数变为完全平方形式,然后再利用根式运算性质;
 解: 解: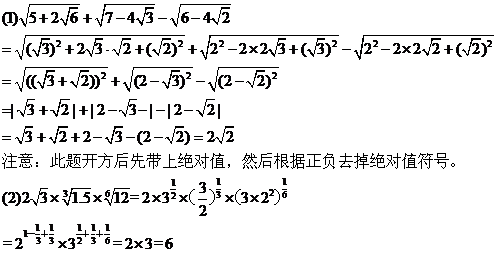 |
要求:例3学生先练习,后讲评,讲评时需向学生强调求值过程中的变形技巧。
(III)课堂练习
计算下列各式:
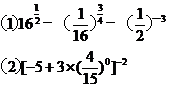
要求:学生板演练习,做完后老师讲评。
(IV)课时小结
通过本节学习,要求大家能够熟练运用有理数幂运算性质进行化简、求值,并掌握一定的解题技巧,如凑完全平方、寻求同底幂等方法。
(V)课后作业
第二教材有关题目
1.分数指数幂的概念,以及有理指数幂的运算性质
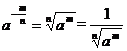 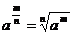 分数指数幂概念
有理指数幂运算性质 分数指数幂概念
有理指数幂运算性质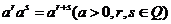 ; ;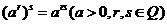 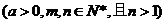
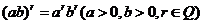 |
3.培养学生的数学应用意识。
教学重点:有理指数幂运算性质运用。
教学难点:化简、求值的技巧
教学方法:启发引导式
教学过程
(I)复习回顾
2.熟练运用有理指数幂运算性质进行化简、求值;
1.掌握根式与分数指数幂的互化;
12. A、B两地相距40km,从A到B两条输电线的总电阻为800Ω,若A、B之间某处E两条输电线发生短路,为查明短路地点,在A处接上电源,测得电压表示数为10V,小量程电流表读数为40mA,如图所示,则短路处距A多远?
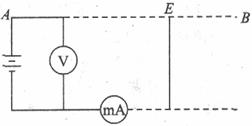
探究:
联系本节所学内容思考并讨论课本“说一说”中体现了哪些物理原理?
学后反思:
你对学案的意见:
课后作业:
问题与练习2、3、4
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com