
1.椭圆
(1)椭圆概念
平面内与两个定点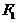 、
、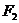 的距离的和等于常数(大于
的距离的和等于常数(大于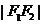 )的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。若
)的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。若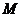 为椭圆上任意一点,则有
为椭圆上任意一点,则有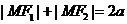
椭圆的标准方程为: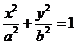 (
(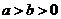 )(焦点在x轴上)或
)(焦点在x轴上)或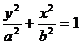 (
(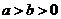 )(焦点在y轴上)。
)(焦点在y轴上)。
注:①以上方程中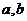 的大小
的大小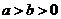 ,其中
,其中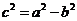 ;
;
②在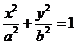 和
和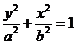 两个方程中都有
两个方程中都有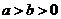 的条件,要分清焦点的位置,只要看
的条件,要分清焦点的位置,只要看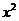 和
和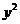 的分母的大小。例如椭圆
的分母的大小。例如椭圆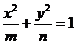 (
(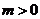 ,
,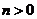 ,
,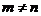 )当
)当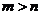 时表示焦点在
时表示焦点在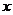 轴上的椭圆;当
轴上的椭圆;当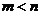 时表示焦点在
时表示焦点在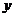 轴上的椭圆
轴上的椭圆
(2)椭圆的性质
①范围:由标准方程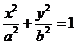 知
知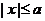 ,
,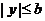 ,说明椭圆位于直线
,说明椭圆位于直线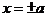 ,
,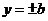 所围成的矩形里;
所围成的矩形里;
②对称性:在曲线方程里,若以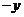 代替
代替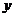 方程不变,所以若点
方程不变,所以若点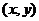 在曲线上时,点
在曲线上时,点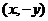 也在曲线上,所以曲线关于
也在曲线上,所以曲线关于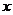 轴对称,同理,以
轴对称,同理,以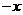 代替
代替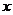 方程不变,则曲线关于
方程不变,则曲线关于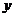 轴对称。若同时以
轴对称。若同时以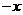 代替
代替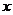 ,
,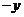 代替
代替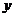 方程也不变,则曲线关于原点对称。
方程也不变,则曲线关于原点对称。
所以,椭圆关于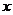 轴、
轴、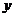 轴和原点对称。这时,坐标轴是椭圆的对称轴,原点是对称中心,椭圆的对称中心叫椭圆的中心;
轴和原点对称。这时,坐标轴是椭圆的对称轴,原点是对称中心,椭圆的对称中心叫椭圆的中心;
③顶点:确定曲线在坐标系中的位置,常需要求出曲线与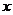 轴、
轴、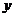 轴的交点坐标。在椭圆的标准方程中,令
轴的交点坐标。在椭圆的标准方程中,令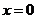 ,得
,得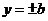 ,则
,则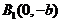 ,
,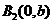 是椭圆与
是椭圆与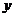 轴的两个交点。同理令
轴的两个交点。同理令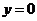 得
得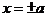 ,即
,即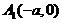 ,
,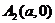 是椭圆与
是椭圆与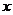 轴的两个交点。
轴的两个交点。
所以,椭圆与坐标轴的交点有四个,这四个交点叫做椭圆的顶点。
同时,线段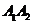 、
、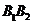 分别叫做椭圆的长轴和短轴,它们的长分别为
分别叫做椭圆的长轴和短轴,它们的长分别为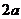 和
和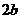 ,
,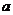 和
和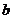 分别叫做椭圆的长半轴长和短半轴长。
分别叫做椭圆的长半轴长和短半轴长。
由椭圆的对称性知:椭圆的短轴端点到焦点的距离为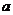 ;在
;在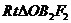 中,
中,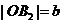 ,
,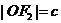 ,
,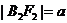 ,且
,且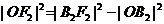 ,即
,即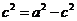 ;
;
④离心率:椭圆的焦距与长轴的比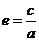 叫椭圆的离心率。∵
叫椭圆的离心率。∵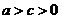 ,∴
,∴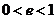 ,且
,且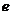 越接近
越接近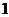 ,
,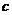 就越接近
就越接近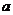 ,从而
,从而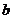 就越小,对应的椭圆越扁;反之,
就越小,对应的椭圆越扁;反之,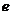 越接近于
越接近于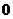 ,
,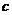 就越接近于
就越接近于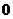 ,从而
,从而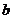 越接近于
越接近于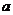 ,这时椭圆越接近于圆。当且仅当
,这时椭圆越接近于圆。当且仅当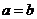 时,
时,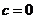 ,两焦点重合,图形变为圆,方程为
,两焦点重合,图形变为圆,方程为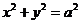 。
。
本讲内容是圆锥曲线的基础内容,也是高考重点考查的内容,在每年的高考试卷中一般有2-3道客观题,难度上易、中、难三档题都有,主要考查的内容是圆锥曲线的概念和性质,从近十年高考试题看主要考察圆锥曲线的概念和性质。圆锥曲线在高考试题中占有稳定的较大的比例,且选择题、填空题和解答题都涉及到,客观题主要考察圆锥曲线的基本概念、标准方程及几何性质等基础知识和处理有关问题的基本技能、基本方法
对于本讲内容来讲,预测2011年:
(1)1至2道考察圆锥曲线概念和性质客观题,主要是求值问题;
(2)可能会考察圆锥曲线在实际问题里面的应用,结合三种形式的圆锥曲线的定义。
3.了解双曲线的定义、几何图形和标准方程,知道双曲线的有关性质
2.经历从具体情境中抽象出椭圆、抛物线 模型的过程,掌握它们的定义、标准方程、几何图形及简单性质;
模型的过程,掌握它们的定义、标准方程、几何图形及简单性质;
1.了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用;
第17届世界杯足球赛于2002年夏季在韩国、日本举办、五大洲共有32支球队有幸参加,他们先分成8个小组循环赛,决出16强(每队均与本组其他队赛一场,各组一、二名晋级16强),这支球队按确定的程序进行淘汰赛,最后决出冠亚军,此外还要决出第三、四名,问这次世界杯总共将进行多少场比赛?
答案是: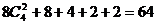 ,这题如果作为习题课应如何分析
,这题如果作为习题课应如何分析
解:可分为如下几类比赛:
⑴小组循环赛:每组有6场,8个小组共有48场;
⑵八分之一淘汰赛:8个小组的第一、二名组成16强,根据抽签规则,每两个队比赛一场,可以决出8强,共有8场;
⑶四分之一淘汰赛:根据抽签规则,8强中每两个队比赛一场,可以决出4强,共有4场;
⑷半决赛:根据抽签规则,4强中每两个队比赛一场,可以决出2强,共有2场;
⑸决赛:2强比赛1场确定冠亚军,4强中的另两队比赛1场决出第三、四名 共有2场.
综上,共有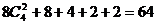 场
场
3.⑴6本不同的书全部送给5人,有多少种不同的送书方法?
⑵5本不同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
⑶5本相同的书全部送给6人,每人至多1本,有多少种不同的送书方法?
答案:⑴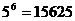 ;⑵
;⑵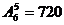 ;⑶
;⑶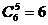 .
.
2.以一个正方体的8个顶点连成的异面直线共有
对
解:由上题可知以一个正方体的顶点为顶点的四面体共有58个,每个四面体的四条棱可以组成3对异面直线,因此以一个正方体的8个顶点连成的异面直线共有3×58=174对
另解: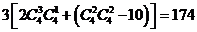 对
对 
1.以一个正方体的顶点为顶点的四面体共有
个 
解:正方体有8个顶点,任取4个顶点的组合数为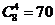 个,
个,
其中四点共面的情况分2类:构成表面的有6组;构成对角面的有6组,
所以,能形成四面体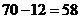 (个).
(个).
10. 女生的人数是2 思路:分
思路:分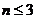 和
和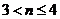 两种情况讨论
两种情况讨论
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com