
4.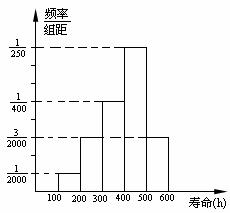 对某种电子元件使用寿命跟踪调查, 抽取容量
对某种电子元件使用寿命跟踪调查, 抽取容量
为1000的样本, 其频率分布直方图如图所示, 根
据此图可知这批样本中电子元件的寿命在300~500
小时的数量是 个.
3. 过原点且倾斜角为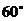 的直线被圆学
的直线被圆学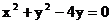 所截得的弦长为科网
.
所截得的弦长为科网
.
2. 设集合 , 则
, 则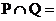 .
.
1. 若命题“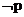 ”与命题“
”与命题“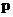 或
或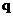 ”都是真命题, 那么命题
”都是真命题, 那么命题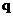 一定是
. 命题 (填写
一定是
. 命题 (填写
“真”或“假”)
2.根式的运算性质:
①当n为任意正整数时,(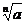 )
) =a.
=a.
②当n为奇数时,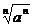 =a;当n为偶数时,
=a;当n为偶数时,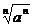 =|a|=
=|a|=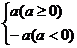 .
.
⑶根式的基本性质: ,(a
,(a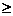 0).
0).
1.根式的概念;
例1(课本第71页 例1)求值
①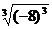 = -8 ;
= -8 ;
②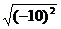 = |-10| =
10 ;
= |-10| =
10 ;
③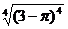 = |
= |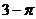 | =
| = 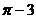 ;
;
④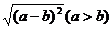 = |a- b| =
a- b .
= |a- b| =
a- b .
去掉‘a>b’结果如何?
例2求值:
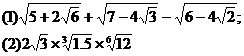
分析:(1)题需把各项被开方数变为完全平方形式,然后再利用根式运算性质;
 解:
解:
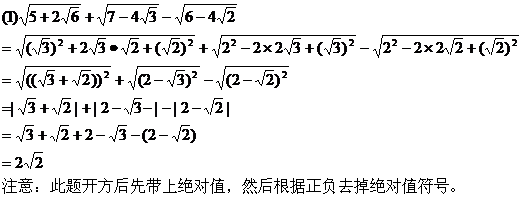
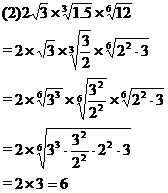

1.根式:
⑴计算(可用计算器)
①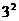 = 9 ,则3是9的平方根 ;
= 9 ,则3是9的平方根 ;
②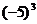 =-125 ,则-5是-125的立方根 ;
=-125 ,则-5是-125的立方根 ;
③若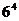 =1296 ,则6是1296 的 4次方根 ;
=1296 ,则6是1296 的 4次方根 ;
④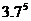 =693.43957 ,则3.7是693.43957的5次方根 .
=693.43957 ,则3.7是693.43957的5次方根 .
⑵定义:
一般地,若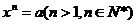 则x叫做a的n次方根
则x叫做a的n次方根
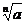 叫做根式,n叫做根指数,a叫做被开方数
叫做根式,n叫做根指数,a叫做被开方数
例如,27的3次方根表示为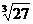 ,-32的5次方根表示为
,-32的5次方根表示为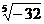 ,
,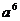 的3次方根表示为
的3次方根表示为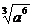 ;16的4次方根表示为!
;16的4次方根表示为!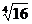 ,即16的4次方根有两个,一个是
,即16的4次方根有两个,一个是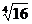 ,另一个是-
,另一个是-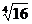 ,它们绝对值相等而符号相反.
,它们绝对值相等而符号相反.
⑶性质:
①当n为奇数时:正数的n次方根为正数,负数的n次方根为负数
记作: 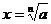

②当n为偶数时,正数的n次方根有两个(互为相反数)
记作: 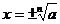

③负数没有偶次方根,
④ 0的任何次方根为0
注:当a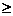 0时,
0时,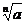
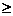 0,表示算术根,所以类似
0,表示算术根,所以类似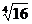 =2的写法是错误的.
=2的写法是错误的.
⑷常用公式
根据n次方根的定义,易得到以下三组常用公式:
①当n为任意正整数时,(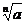 )
) =a.例如,(
=a.例如,(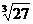 )
)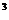 =27,(
=27,(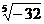 )
)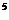 =-32.
=-32.
②当n为奇数时,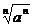 =a;当n为偶数时,
=a;当n为偶数时,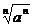 =|a|=
=|a|=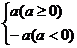 .
.
例如,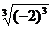 =-2,
=-2,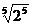 =2;
=2;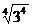 =3,
=3,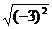 =|-3|=3.
=|-3|=3.
⑶根式的基本性质: ,(a
,(a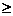 0).
0).
注意,⑶中的a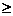 0十分重要,无此条件则公式不成立. 例如
0十分重要,无此条件则公式不成立. 例如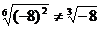 .
.
用语言叙述上面三个公式:
⑴非负实数a的n次方根的n次幂是它本身.
⑵n为奇数时,实数a的n次幂的n次方根是a本身;n为偶数时,实数a的n次幂的n次方根是a的绝对值.
⑶若一个根式(算术根)的被开方数是一个非负实数的幂,那么这个根式的根指数和被开方数的指数都乘以或者除以同一个正整数,根式的值不变.
3.注意
①
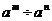 可看作
可看作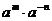 ∴
∴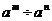 =
=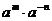 =
=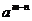

②
 可看作
可看作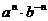 ∴
∴ =
=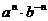 =
=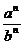

2.运算性质:
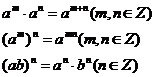

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com