
5.已知向量a=(1,2),b=(2,-3).若向量c满足(c+a)//b,c⊥(a+b),则c=
A.(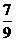 ,
, ) B.(-
) B.(- ,-
,-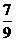 ) C.(
) C.( ,
,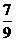 ) D.(-
) D.(-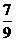 ,-
,- )
)
4.设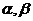 是两个不同的平面,
是两个不同的平面,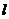 是一条直线,以下命题正确的是
是一条直线,以下命题正确的是
A.若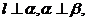 则
则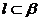 B.若
B.若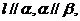 则
则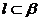
C.若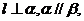 则
则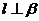 D.若
D.若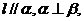 则
则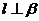
3.设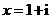 (
(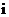 是虚数单位),则
是虚数单位),则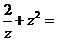
A.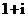 B.
B.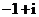 C.
C.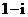 D.
D.
2.“ ”是“
”是“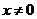 ”的
”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
1.设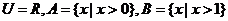 ,则
,则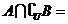
A. B.
B.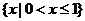 C.
C.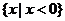 D.
D.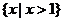
22.(本题满分15分)已知抛物线C:x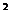 =2py(p>0)上一点A(m,4)到其焦点的距离为
=2py(p>0)上一点A(m,4)到其焦点的距离为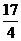 .
.
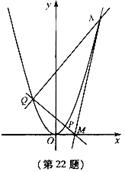 (I)求p于m的值;
(I)求p于m的值;
(Ⅱ)设抛物线C上一点p的横坐标为t(t>0),过p的直线交C于另一点Q,交x轴于M点,过点Q作PQ的垂线交C于另一点N.若MN是C的切线,求t的最小值;
21.(本题满分15分)已知函数f(x)=x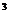 +(1-a) x
+(1-a) x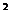 -a(a+2)x+b(a,b
-a(a+2)x+b(a,b R).
R).
(I)若函数f(x)的图像过原点,且在原点处的切线斜率是-3,求a,b的值;
(Ⅱ)若函数f(x)在区间(-1,1)上不单调,求a的取值范围. 

20.(本题满分14分)设 为数列
为数列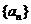 的前n项和,
的前n项和,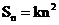 +n,n
+n,n N
N ,其中k是常数.
,其中k是常数.
(I)求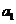 及
及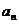 ;
;
(Ⅱ)若对于任意的m N
N ,a
,a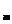 ,a
,a ,a
,a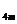 成等比数列,求k的值.
成等比数列,求k的值.
19. (本题满分14分)如图,DC
(本题满分14分)如图,DC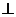 平面ABC,EB∥DC,AC=BC=EB=2DC=2,
平面ABC,EB∥DC,AC=BC=EB=2DC=2,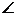 ACB=120°,P,Q分别为AE,AB的中点.
ACB=120°,P,Q分别为AE,AB的中点.
(Ⅰ)证明:PQ∥平面ACD;
(Ⅱ)求AD与平面ABE所成角的正弦值.
18.(本题满分14分)在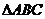 中,角A,B,C所对的边分别为a,b,c,且满足
中,角A,B,C所对的边分别为a,b,c,且满足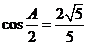 ,
,
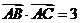 .
.
(Ⅰ)求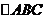 的面积;
的面积; 

(Ⅱ)若c=1,求a的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com