
5、蒸馒头时,在发酵面团中加入某种物质,既能除去面团中的酸,又使馒松软,加入的这种物质是( )
A、NaOH B、Na2CO3 C、CaO D、NaCl
4、农作物收割后留下大量秸杆,下列有关秸杆的处理方法中错误的是 ( )
A、做饲料 B、制沼气 C、造纸 D、就地焚烧
3、报载一辆满载浓硫酸的槽罐车在路上因车祸翻倒,浓硫酸大量泄露。为了不污染旁边的水源,下列采取的措施适宜的是 ( )
A. 用水冲洗泄露的浓硫酸 B. 将熟石灰撒在泄露的浓硫酸上
C. 将氧化钡撒在泄露的浓硫酸上 D. 用土将泄露的浓硫酸掩埋
2、可降解塑料是指在自然条件下能够自行分解的塑料。研制、生产可降解塑料的主要目的是 ( )
A. 节省制造塑料的原料 B. 便于加工塑料产品
C. 扩大塑料使用范围 D. 解决“白色污染”问题
1、为了增强市民环保意识,变废为宝,在城市率先实行垃圾分类回收。通常,绿色箱用来装可回收再利用垃圾,黄色箱用来装不可回收垃圾。以下能扔进绿色垃圾箱的是( )
①废旧报纸 ②废铜钱 ③一次性塑料盒 ④口香糖渣 ⑤果皮 ⑥空矿泉水瓶 ⑦废铁锅
A. ①③⑤⑦ B. ③④⑤⑥ C. ①②⑤⑦ D. ①②⑥⑦
5、认识化学与社会发展的重要性。 二、典型题例与解析:
例1.由于不重视环境保护,某市一条长约150km的作为饮用水源的河水受到严重污染,被污染的河水pH在2~6之间,河水中氮、磷、铅的含量都超过可作为
饮用水源的I类、II类地表水的标准。国家环境保护总局发布的《地表水环境质量标准》,对地表水质量作了明确规定,部分指标如下(除pH外,各项目的单位:mg/L):
项目及标准水质分类
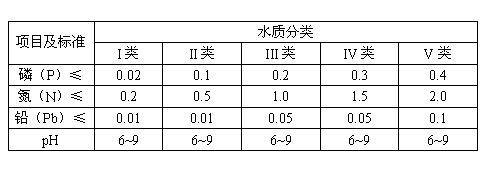
(l)如果让你测定该河水样的酸碱度,应选用______。
A. 石蕊试液 B. 酚酞试液
C. pH试纸 D. 碳酸钠溶液
(2)针对上表中的各项指标,如果要防止自然界中的II类水质变为III类水质,在
我们的生活中应采取的主要措施是(写出两点即可)___________________。
(3)某化学兴趣小组要研究被污染的河水对植物生长的影响,他们设计了以下实验:在相邻的两块土质、周边环境、面积一样的土壤上同时种植了同品种、同数量、同样生长状况的向日葵,一块浇被污染的河水,一块浇未被污染的河水,其余的栽培条件都一样,对照观察两块地上向日葵的生长情况,你认为他们的实验设计合理吗?_____________,理由____________________。
解析:解此题的关键在于了解水资源的污染和治理,能应用这些知识解决环境保护中的实际问题。水质分为五类,被污染的水中N、P、Pb超标,不能饮用。进行对照实验时要注意控制变量,除一个变量不同外,其余条件相同。
例2.人类能自主补充食物转化成能源来维持生命活动,而机器人主要是靠事先储存的电能来进行活动的,但目前科学家已制造出了一种能捕食苍蝇的生态机器人,它能将捕到的苍蝇体内的糖类物质通过微生物燃料电池直接转化为电能,供自身活动需要。请回答下
列问题:
(1)糖类物质属于_____物质,生态机器人的能量转化形式是从_______能转化为电能。
(2)在实验中,质量为20kg的生态机器人吃了8只苍蝇,用5天时间匀速移动了10m,若机器人受到的阻力是该机器人体重的0.l倍,则该机器人克服阻力做的功是________。
(3)除这种以捕食生物为食的生态机器人外,如果设计一种可从自然界中较方便地自主补充能量再转化为电能的机器人,你设计的机器人直接从自然界补充的能量形式是_______,获得这种能量的方法(途径)是在机器人上安装________。
解析:这是一道关于能量转化方面的实际应用题,涉及前沿科学,即机器人怎样将生物能转化为化学能。同时也是一道学科交叉题,通过生物能转化为化学能,最后转变为机械能做功。很显然,机械能做功要用到公式W=F·S。解决能源问题的关键是向太阳要能,向大自然要能,开发新能源、再生能,减少污染,实现可持续发展。
例3. 随着我国航天科技水平的迅速发展,探测火星已成为我国航天科技发展的远景目标,但要把人类送上火星,还有许多航天技术问题需要解决。如:如何提供在往返路程中航天员呼吸所需要的氧气和消除呼吸过程产生的二氧化碳就是一个值得研究的问题。已知一个成年人平均每年要呼吸空气6 570 000L左右,而目前的飞船飞往火星来回一趟需两年的时间,如果在飞船发射时携带所需的氧气,则质量很大,将大大提高发射的成本和难度。
(1)若飞船上有三名航天员,请计算来回火星一趟,理论上需要氧气__________kg。(氧气的密度是1.43g/L,答案取整数)
(2)有人提出在飞船上供氧的两个方案: ①通过太阳能电池产生的电流来电解水。
②通过下列化学反应产生氧气:2Na2O + 2CO2 =2Na2CO3 + O2↑ 从减少飞船发射质量和消除呼吸过程产生的二氧化碳的角度,请你评价这两个方案最主要的优缺点(各写一点)。
(3)也有科学家提出研究使航天员人工冬眠的技术或加快飞船速度,缩短航行时间来减少氧气的携带量。你是否有较好的方案,请举一例: 。你提出该方案的简要理由:
解析:题目提示要从两方面去考虑问题。从CO2的循环处理来看,方案②要优于方案①,但通过计算可知,产生同质量的O2,方案②消耗原料质量大,发射成本高,从这点看,方案①要优于方案②。我们最熟悉的CO2与O2之间的循环就是植物的光合作用了,它与人的呼吸作用过程恰好相反,且成本低,简单易行。
4、合理开发和利用资料,树立保护环境与自然和谐相处的意识。
1、认识能源与材料的利用。 2、了解日常生活熟知的合成材料以及应用。 3、了解化学物质与人体健康及环境的关系。
2.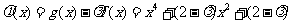 .
.
若满足条件的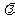 存在,则
存在,则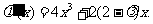
∵函数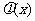 在
在 内是减函数,∴当
内是减函数,∴当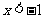 时,
时,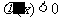 ,
,
即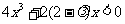 对于
对于 恒成立.
恒成立.
∴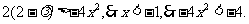
∴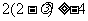 ,解得
,解得 .
.
又函数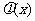 在(-1,0)上是增函数,∴当
在(-1,0)上是增函数,∴当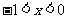 时,
时,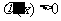
即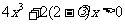 对于
对于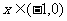 恒成立,
恒成立,
∴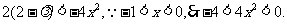
∴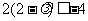 ,解得
,解得 .
.
故当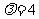 时,
时,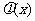 在
在 上是减函数,在(-1,0)上是增函数,即满足条件的
上是减函数,在(-1,0)上是增函数,即满足条件的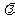 存在.
存在.
说明:函数思维实际上是辩证思维的一种特殊表现形式,它包含着运动、变化,也就存在着量与量之间的相互依赖、相互制约的关系.因此挖掘题目中的隐含条件则是打开解题思路的重要途径,具体到解题的过程,学生很大的思维障碍是迷失方向,不知从何处入手去沟通已知与未知的关系,使分散的条件相对集中,促成问题的解决.不善于应用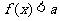 恒成立
恒成立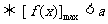 和
和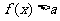 恒成立
恒成立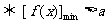 ,究其原因是对函数的思想方法理解不深.
,究其原因是对函数的思想方法理解不深.
利用导数比较大小
例 已知a、b为实数,且 ,其中e为自然对数的底,求证:
,其中e为自然对数的底,求证: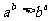 .
.
分析:通过考察函数的单调性证明不等式也是常用的一种方法.根据题目自身的特点,适当的构造函数关系,在建立函数关系时,应尽可能选择求导和判断导数都比较容易的函数,一般地,证明 ,可以等价转化为证明
,可以等价转化为证明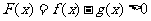 ,如果
,如果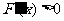 ,则函数
,则函数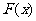 在
在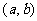 上是增函数,如果
上是增函数,如果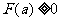 ,由增函数的定义可知,当
,由增函数的定义可知,当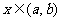 时,有
时,有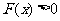 ,即
,即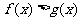 .
.
解:证法一:
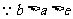 ,∴要证
,∴要证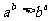 ,只要证
,只要证 ,
,
设 ,则
,则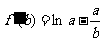 .
.
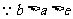 ,∴
,∴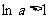 ,且
,且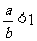 ,∴
,∴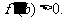
∴函数 在
在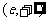 上是增函数.
上是增函数.
∴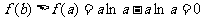 ,即
,即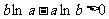 ,
,
∴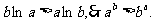
证法二:要证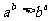 ,只要证
,只要证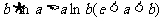 ,
,
即证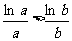 ,设
,设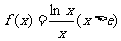 ,则
,则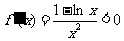 ,
,
∴函数 在
在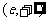 上是减函数.
上是减函数.
又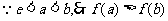 ,即
,即
说明:“构造”是一种重要而灵活的思维方式,应用好构造思想解题的关键是:一要有明确的方向,即为什么目的而构造;二是要弄清条件的本质特点,以便重新进行逻辑组合.解决这种问题常见的思维误区是不善于构造函数或求导之后得出 的错误结论.
的错误结论.
判断函数在给定区间上的单调性
例 函数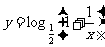 在区间
在区间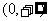 上是( )
上是( )
A.增函数,且 B.减函数,且
B.减函数,且
C.增函数,且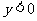 D.减函数,且
D.减函数,且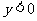
分析:此题要解决两个问题:一是要判断函数值y的大小;二是要判断此函数的单调性.
解:解法一:令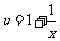 ,且
,且 ,
,
则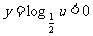 ,排除A、B.
,排除A、B.
由复合函数的性质可知,u在 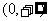 上为减函数.
上为减函数.
又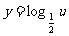 亦为减函数,故
亦为减函数,故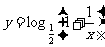 在
在 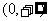 上为增函数,排除D,选C.
上为增函数,排除D,选C.
解法二:利用导数法
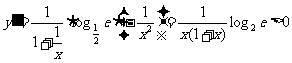
(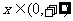 ),故y在
),故y在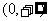 上是增函数.
上是增函数.
由解法一知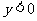 .所以选C.
.所以选C.
说明:求函数的值域,是中学教学中的难关.一般可以通过图象观察或利用不等式性质求解,也可以用函数的单调性求出最大、最小值等(包括初等方法和导数法).对于复合函数的单调性问题,简单的复合函数是可以利用复合函数的性质进行判断,但是利用导数法判断一些较复杂的复合函数还是有很大优势的.
2.设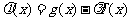 ,试问:是否存在实数
,试问:是否存在实数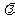 ,使
,使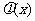 在
在 内为减函数,且在(-1,0)内是增函数.
内为减函数,且在(-1,0)内是增函数.
分析:根据题设条件可以求出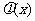 的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数
的表达式,对于探索性问题,一般先对结论做肯定存在的假设,然后由此肯定的假设出发,结合已知条件进行推理论证,由推证结果是否出现矛盾来作出判断.解题的过程实质是一种转化的过程,由于函数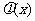 是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数
是可导函数,因此选择好解题的突破口,要充分利用函数的单调性构造等价的不等式,确定适合条件的参数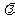 的取值范围,使问题获解.
的取值范围,使问题获解.
解:1.由题意得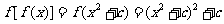 ,
,
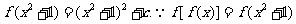 ,
,
∴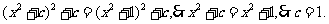
∴
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com