18、解：(1).　　　　　　　　

　 (2)，　　　　　　　　　

　　 ，

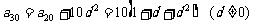当时，.　　　　　　　 　

　 (3)所给数列可推广为无穷数列，其中是首项为1，公差为1的

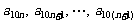等差数列，当时，数列是公差为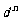的等差数列.　 　

研究的问题可以是：

试写出关于的关系式，并求的取值范围.

研究的结论可以是：由，

　　 　　　　　依次类推可得　

　 　　　　　　当时，的取值范围为等.　 　　　　

17、假设，则

容易看出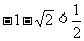，下面证明。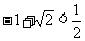

要证：，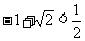

只需证：，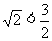

只需证：

上式显然成立，故有。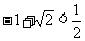

综上，。而这与已知条件相矛盾，

因此假设不成立，也即原命题成立。

16、证明:

　　　　　　 故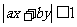

15、证明：

　由正弦定理得：

14、______________

13、…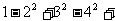

12、

11、____14__________

18、已知数列，其中是首项为1，公差为1的等差数列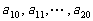；是公差为的等差数列；是公差为的等差数列().

(1)若，求；

(2)试写出关于的关系式，并求的取值范围；

(3)续写已知数列，使得是公差为的等差数列，……，依次类推，把已知数列推广为无穷数列. 提出同(2)类似的问题((2)应当作为特例)，并进行研究，你能得到什么样的结论？

高二数学选修1-2《推理与证明测试题》答案提示

1--10、　 DCABD　　 BAABC

17、用反证法证明：如果，那么。