80．你现在已掌握几种三角形面积的计算公式？

2．当A为锐角时，如果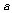≥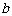，那么只有一解；如果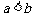，那么可以分下面三种情况来讨论：(1)若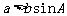，则有两解；(2)若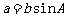，则只有一解；(3)若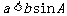，则无解。(以上解答过程详见课本第9－10页))

79．注意在已知三角形的两边及其中一边的对角解三角形时，只有当A为锐角且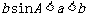时，有两解；其它情况时则只有一解或无解。

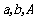例如：在ABC中，已知，讨论三角形解的情况：先由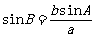可进一步求出B；则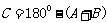从而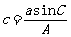1．当A为钝角或直角时，必须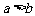才能有且只有一解；否则无解。

78．余弦定理的作用又是什么？

余弦定理及其推论的基本作用为：①已知三角形的任意两边及它们的夹角就可以求出第三边；②已知三角形的三条边就可以求出其它角。

77．正弦定理有何作用？

(1)正弦定理说明同一三角形中，边与其对角的正弦成正比，且比例系数为同一正数，即存在正数k使；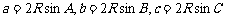

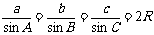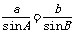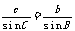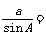
(2)等价于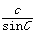，，从而知正弦定理的基本作用为：①已知三角形的任意两角及其一边可以求其他边，如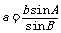；②已知三角形的任意两边与其中一边的对角可以求其他角的正弦值，如。

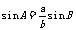76．若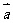与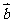的夹角θ，且θ为钝角，则cosθ<0对吗？(必须去掉反向的情况)

　(必修5)

75．如何求向量的模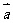？在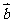方向上的投影为什么？

74．若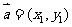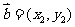，，则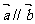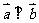，的充要条件是什么？

73．在利用三角函数表示直线的倾斜角、两向量的夹角、两条异面直线所成的角等时，你是否注意到它们各自的取值范围及意义？

①异面直线所成的角、直线与平面所成的角、二面角的取值范围依次是；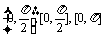

②直线的倾斜角、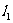与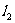的夹角的取值范围依次是；

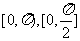③向量的夹角的取值范围是[0，π]

例：设向量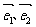 满足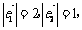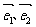的夹角为60⁰，若向量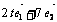与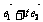的夹角为钝角，则实数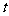的取值范围是　　　　 。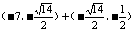

72．辅助角公式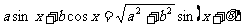：(其中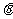角所在的象限由a, b 的符号确定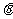，角的值由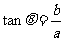确定)在求最值、化简时起着重要作用.