
2.为了得到函数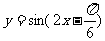 的图象,可以将函数
的图象,可以将函数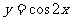 的图象(B )
的图象(B )
(A)向右平移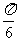 个单位长度 (B)向右平移
个单位长度 (B)向右平移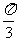 个单位长度
个单位长度
(C)向左平移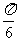 个单位长度 (D)向左平移
个单位长度 (D)向左平移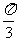 个单位长度
个单位长度
1.若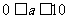 ,则满足
,则满足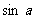 =0.5的角
=0.5的角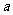 的个数是(C)
的个数是(C)
(A)2 (B)3 (C) 4 (D)5
例5. 求函数 的最小值。
的最小值。
错解 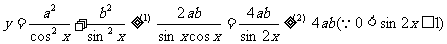
∴当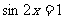 时,
时,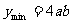
分析:在已知条件下,(1)、(2)两处不能同时取等号。
正解: 
当且仅当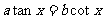 ,即
,即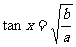 ,时,
,时,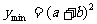
专题四:三角函数
[经典题例]
例1:点P从(1,0)出发,沿单位圆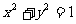 逆时针方向运动
逆时针方向运动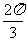 弧长到达Q点,则Q点的坐标为( )
弧长到达Q点,则Q点的坐标为( )
(A) (B)
(B)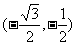 (C)
(C)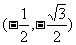 (D)
(D)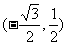
[思路分析] 记 ,由三角函数定义可知Q点的坐标
,由三角函数定义可知Q点的坐标 满足
满足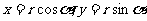 ,故选(A)
,故选(A)
[简要评述]三角函数定义是三角函数理论的基础,理解掌握能起到事半功倍的效果。
例2:求函数 的最小正周期、最大值和最小值.
的最小正周期、最大值和最小值.
[思路分析]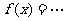
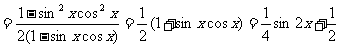
所以函数f(x)的最小正周期是π,最大值是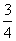 ,最小值是
,最小值是 .
.
[简要评述]三角恒等变形是历年高考考察的主要内容,变形能力的提高取决于一定量的训练以及方法的积累,在此例中“降次、化同角”是基本的思路。此外,求函数的周期、最值是考察的热点,变形化简是必经之路。
例3:已知 ,
,
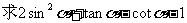 的值.
的值.
[思路分析] ∵ 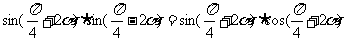
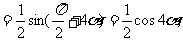 ∴得
∴得 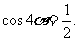 又
又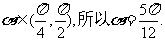
于是 
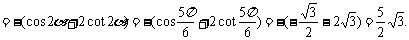
[简要评述] 此类求值问题的类型是:已知三角方程,求某三角代数式的值。一般来说先解三角方程,得角的值或角的某个三角函数值。如何使解题过程化繁为简,变形仍然显得重要,此题中巧用诱导公式、二倍角公式,还用到了常用的变形方法,即“化正余切为正余弦”。
例4:已知b、c是实数,函数f(x)=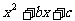 对任意α、β
对任意α、β R有:
R有: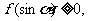
且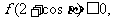
(1)求f(1)的值;(2)证明:c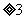 ;(3)设
;(3)设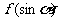 的最大值为10,求f(x)。
的最大值为10,求f(x)。
[思路分析](1)令α= ,得
,得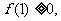 令β=
令β=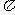 ,得
,得 因此
因此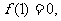 ;
;
(2)证明:由已知,当 时,
时,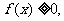 当
当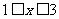 时,
时,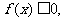 通过数形结合的方法可得:
通过数形结合的方法可得: 化简得c
化简得c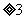 ;
;
(3)由上述可知,[-1,1]是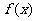 的减区间,那么
的减区间,那么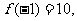 又
又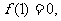 联立方程组可得
联立方程组可得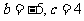 ,所以
,所以
[简要评述]三角复合问题是综合运用知识的一个方面,复合函数问题的认识是高中数学学习的重点和难点,这一方面的学习有利于提高综合运用的能力。
例5:关于正弦曲线回答下述问题:
(1)函数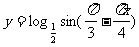 的单调递增区间是
的单调递增区间是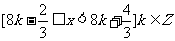 ;
;
(2)若函数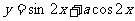 的图象关于直线
的图象关于直线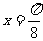 对称,则
对称,则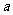 的值是 1 ;
的值是 1 ;
(3)把函数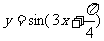 的图象向右平移
的图象向右平移 个单位,再将图象上各点的横坐标扩大到原来的3倍(纵坐标不变),则所得的函数解析式子是
个单位,再将图象上各点的横坐标扩大到原来的3倍(纵坐标不变),则所得的函数解析式子是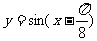 ;
;
(4)若函数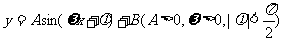 的最大值是
的最大值是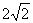 ,最小值是
,最小值是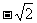 ,最小正周期是
,最小正周期是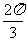 ,图象经过点(0,-
,图象经过点(0,-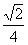 ),则函数的解析式子是
),则函数的解析式子是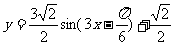 ;
;
[思路分析] 略
[简要评述]正弦曲线问题是三角函数性质、图象问题中的重点内容,必须熟练掌握。上述问题的解答可以根据正弦曲线的“五点画法”在草稿纸上作出函数的草图来验证答案或得到答案。
例6:函数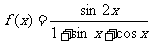
(1)求f(x)的定义域;(2)求f(x)的最大值及对应的x值。
[思路分析] (1){x|x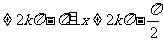
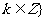
(2)设t=sinx+cosx, 则y=t-1 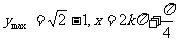
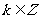
[简要评述]若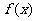 关于
关于 与
与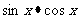 的表达式,求函数的最值常通过换元法,如令
的表达式,求函数的最值常通过换元法,如令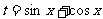 ,使问题得到简化。
,使问题得到简化。
例7:在ΔABC中,已知 (1)求证:a、b、c成等差数列;(2)求角B的取值范围。
(1)求证:a、b、c成等差数列;(2)求角B的取值范围。
[思路分析](1)条件等式降次化简得
(2)
∴……,得B的取值范围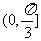
[简要评述]三角形中的变换问题,除了需要运用三角式变换的所有方法、技巧外,还经常需要考虑对条件或结论中的“边”与“角”运用“正弦定理、余弦定理或面积公式”进行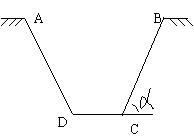 互换。
互换。
例8:水渠横断面为等腰梯形,如图所示,渠道深为h,梯形面积为S,为了使渠道的渗水量达到最小,应使梯形两腰及下底之和达到最小,此时下底角α应该是多少?
[思路分析] CD=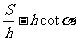 , C=
, C=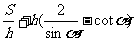 ,转化为考虑y=
,转化为考虑y=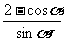 的最小值,可得当
的最小值,可得当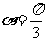 时,y最小,即C最小。
时,y最小,即C最小。
[简要评述]“学以致用”是学习的目的之一,三角知识的应用很广泛,在复习过程中应受到重视。
[热身冲刺]
例4. 设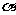 、
、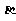 为锐角,且
为锐角,且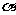 +
+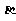
 ,讨论函数
,讨论函数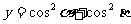 的最值。
的最值。
错解 
可见,当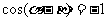 时,
时,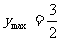 ;当
;当 时,
时, 。
。
分析:由已知得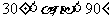 ,∴
,∴ ,则
,则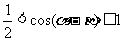
∴当 ,即
,即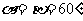 时,
时, ,最大值不存在。
,最大值不存在。
例3. 若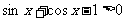 ,求
,求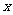 的取值范围。
的取值范围。
错解 移项得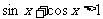 ,两边平方得
,两边平方得
即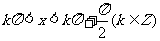
分析:忽略了满足不等式的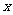 在第一象限,上述解法引进了
在第一象限,上述解法引进了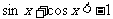 。
。
正解: 即
即 ,由
,由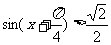 得
得
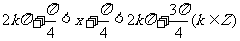 ∴
∴
例2. 已知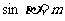 ,求
,求 的值及相应
的值及相应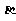 的取值范围。
的取值范围。
错解 当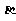 是第一、四象限时,
是第一、四象限时,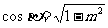 ,当
,当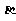 是第二、三象限时,
是第二、三象限时,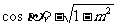 。
。
分析:把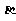 限制为象限角时,只考虑
限制为象限角时,只考虑 且
且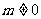 的情形,遗漏了界限角。应补充:当
的情形,遗漏了界限角。应补充:当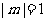 时,
时,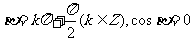 ;当
;当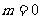 时,
时,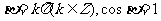 ,或
,或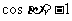 。
。
例1. 若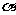 、
、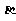 为第三象限角,且
为第三象限角,且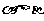 ,则( )
,则( )
(A) (B)
(B)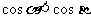 (C)
(C)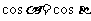 (D)以上都不对
(D)以上都不对
错解 选(A)
分析:角的概念不清,误将象限角看成类似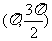 区间角。如取
区间角。如取 ,可知(A)不对。用排除法,可知应选(D)。
,可知(A)不对。用排除法,可知应选(D)。
20.设平面上有直线 ,曲线
,曲线 。又有下列方式定义数列
。又有下列方式定义数列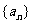 :
:
(1) ;(2)当给定
;(2)当给定 后,作过点
后,作过点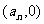 且与
且与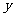 轴平行的直线,它与
轴平行的直线,它与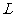 的交点记为
的交点记为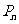 ;再过点
;再过点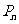 且与
且与 轴平行的直线,它与
轴平行的直线,它与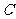 的交点记为
的交点记为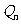 ,定义
,定义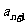 为
为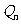 的横坐标。试求数列
的横坐标。试求数列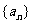 的通项,并计算
的通项,并计算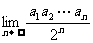 。
。
解:显然,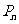 的坐标可写为
的坐标可写为 ,
,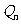 的坐标写为
的坐标写为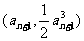 ,故有
,故有 ,
,
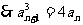 ,两边取对数并整理得:
,两边取对数并整理得: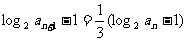 , 从而得
, 从而得
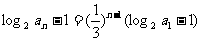 ,即
,即 ,
,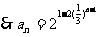 ,
,
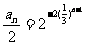 ,
,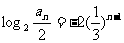 ,
,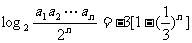 ,
,
 。
。
19.设函数 的最小值为
的最小值为 ,最大值为
,最大值为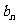 ,且
,且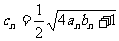 。
。
(1)求数列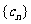 的通项公式;
的通项公式;
(2)设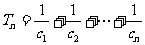 ,求证:
,求证: 。
。
解:(1)由已知函数式可得, ,由已知可知
,由已知可知 ,令
,令 ,得
,得 ,
, 已知函数最小值为
已知函数最小值为 ,最大值为
,最大值为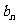 ,
,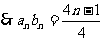 ,
,
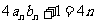 ,
, 。
。
(2)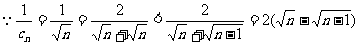 ,
,
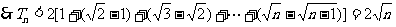 。
。
又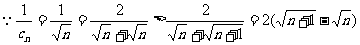 ,
,
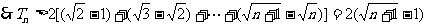 。
。
因此, 。
。
18.假设 型汽车关税在
型汽车关税在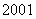 年是
年是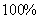 ,在
,在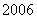 年是
年是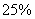 ,
,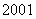 年
年 型进口车每辆价格为
型进口车每辆价格为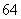 万元(其中含
万元(其中含 万元关税税款)。
万元关税税款)。
(1)已知与 型车性能相近的
型车性能相近的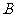 型国产车,
型国产车,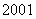 年的价格为
年的价格为 万元,若
万元,若 型车的价格只受关税降低的影响,为了保证在
型车的价格只受关税降低的影响,为了保证在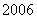 年
年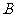 型车的价格不高于
型车的价格不高于 型车价格的
型车价格的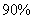 ,
,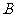 型车的价格要逐年降低,问平均每年至少下降多少万元?
型车的价格要逐年降低,问平均每年至少下降多少万元?
(2)某人在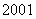 年将
年将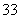 万元存入银行,假设该银行扣利息税后的年利率为
万元存入银行,假设该银行扣利息税后的年利率为 (五年内不变),且每年按复利计算(例如,第一年的利息记入第
(五年内不变),且每年按复利计算(例如,第一年的利息记入第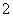 年的本金),那么五年到期时这笔钱连本带息是否一定够买一辆(1)中所述降价后的
年的本金),那么五年到期时这笔钱连本带息是否一定够买一辆(1)中所述降价后的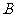 型汽车?
型汽车?
解:(1)因为 型车
型车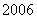 年关税税款为
年关税税款为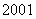 年关税税款的
年关税税款的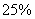 ,故所减少了的关税税款为
,故所减少了的关税税款为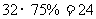 (万元)。所以,
(万元)。所以,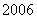 年
年 型车的价格为
型车的价格为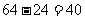 (万元)。
(万元)。
因为在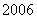 年
年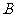 型车的价格不高于
型车的价格不高于 型车价格的
型车价格的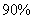 ,所以有:
,所以有: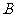 型车价格
型车价格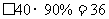 (万元)。因为
(万元)。因为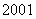 年
年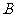 型车的价格为
型车的价格为 万元,故五年中至少要降价
万元,故五年中至少要降价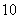 万元。所以平均每年至少降价
万元。所以平均每年至少降价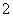 万元。
万元。
(2)根据题意,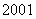 年存入的
年存入的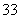 万元
万元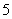 年后到期时连本带息可得
年后到期时连本带息可得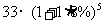 (万元)。
(万元)。
因为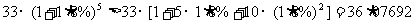 (万元),所以够买一辆(1)中所述降价后的
(万元),所以够买一辆(1)中所述降价后的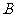 型汽车。
型汽车。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com