
8.(2006福建) 已知函数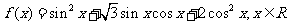
(I)求函数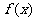 的最小正周期和单调增区间;
的最小正周期和单调增区间;
(II)函数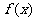 的图象可以由函数
的图象可以由函数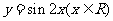 的图象经过怎样的变换得到?
的图象经过怎样的变换得到?
解:(I)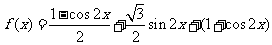
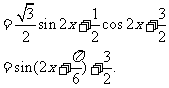
 的最小正周期
的最小正周期
由题意得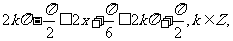
即 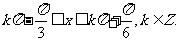
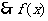 的单调增区间为
的单调增区间为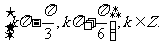
(II)方法一:
先把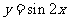 图象上所有点向左平移
图象上所有点向左平移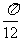 个单位长度,得到
个单位长度,得到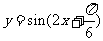 的图象,再把所得图象上所有的点向上平移
的图象,再把所得图象上所有的点向上平移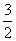 个单位长度,就得到
个单位长度,就得到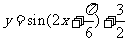 的图象。
的图象。
方法二:
把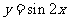 图象上所有的点按向量
图象上所有的点按向量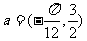 平移,就得到
平移,就得到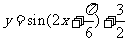 的图象。
的图象。

7. (2006山东)已知函数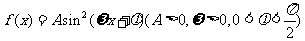 ,且
,且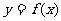 的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
的最大值为2,其图象相邻两对称轴间的距离为2,并过点(1,2).
(I)求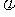
(II)计算 .
.
解:(I)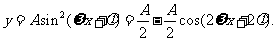
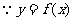 的最大值为2,
的最大值为2, .
.
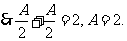
又 其图象相邻两对称轴间的距离为2,
其图象相邻两对称轴间的距离为2, ,
,
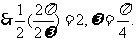
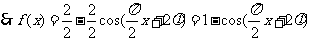 .
.
 过
过 点,
点,
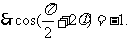

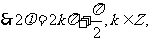
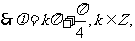
又
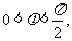
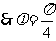 .
.
(II)解法一: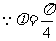 ,
,
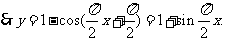
 .
.
又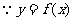 的周期为4,
的周期为4, ,
,
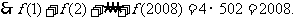
解法二: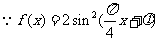
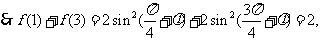
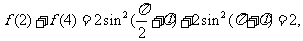
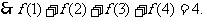
又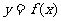 的周期为4,
的周期为4,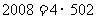 ,
,
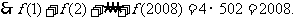
6.(2005上海)函数 的图象与直线
的图象与直线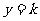 有且仅有两个不同的交点,则
有且仅有两个不同的交点,则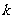 的取值范围是__________。
的取值范围是__________。
✿练习简答:1-4.DACA;5. (1,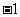 ); 6.
); 6. 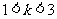 .
.
[解答题]
5.(2006湖南)若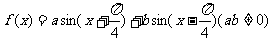 是偶函数, 则有序实数对
是偶函数, 则有序实数对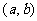 可以是__________.(注: 写出你认为正确的一组数字即可)
可以是__________.(注: 写出你认为正确的一组数字即可)
4.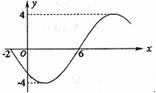 函数
函数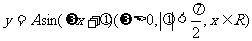 的部分图象如图所示,则函数表达式为 ( )
的部分图象如图所示,则函数表达式为 ( )
(A)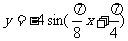 (B)
(B)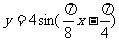
(C)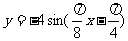 (D)
(D)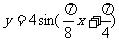
[填空题]
3.(2006江苏)为了得到函数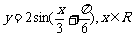 的图像,只需把函数
的图像,只需把函数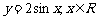 的图像上所有的点 ( )
的图像上所有的点 ( )
(A)向左平移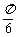 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的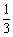 倍(纵坐标不变)
倍(纵坐标不变)
(B)向右平移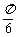 个单位长度,再把横坐标缩短到原来的
个单位长度,再把横坐标缩短到原来的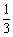 倍(纵坐标不变)
倍(纵坐标不变)
(C)向左平移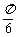 个单位长度,再把横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把横坐标伸长到原来的3倍(纵坐标不变)
(D)向右平移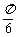 个单位长度,再把横坐标伸长到原来的3倍(纵坐标不变)
个单位长度,再把横坐标伸长到原来的3倍(纵坐标不变)
2.已知函数y=tan(2x+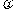 )的图象过点(
)的图象过点(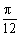 ,0),则
,0),则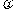 可以是 ( )
可以是 ( )
A.-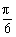 B.
B.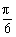 C.-
C.-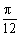 D.
D.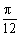
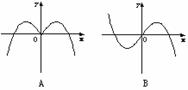
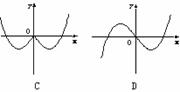
1.函数y=-xcosx的部分图象是 ( )
4.数形结合,数形转化是本课的重要的思想方法。
同步练习 4.4 三角函数的图象 解析式
[选择题]
3.深刻理解图象变换与函数式变换(参数变化)的关系,掌握由图象求解析式的方法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com