
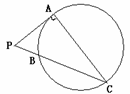
15.(几何证明选讲选做题)已知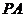 是圆
是圆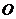 的切线,切点为
的切线,切点为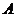 ,
, .
.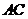 是圆
是圆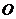 的直径,
的直径, 与圆
与圆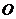 交于点
交于点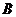 ,
,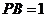 ,则圆
,则圆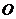 的半径
的半径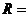 .
.
 [标准答案]
[标准答案]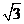 。
。
[试题解析]依题意,我们知道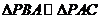 ,由相似三角形的性质我们有
,由相似三角形的性质我们有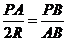 ,即
,即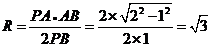 。
。
[高考考点]几何证明选讲.
(2008广东文)
14.(不等式选讲选做题)已知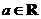 ,若关于
,若关于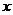 的方程
的方程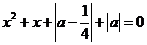 有实根,则
有实根,则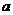 的取值范围是
.
的取值范围是
.
[标准答案]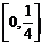 。
。
[试题解析]关于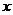 的二次方程的判别式
的二次方程的判别式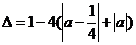 ,方程有实根,那么
,方程有实根,那么
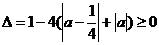 。
。
即 ,而
,而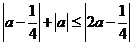 ,从而
,从而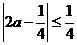 ,
,
解得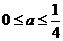 。
。
[高考考点]不等式选讲。
13.(2008广东理)(坐标系与参数方程选做题)已知曲线 的极坐标方程分别为
的极坐标方程分别为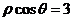 ,
,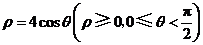 ,则曲线
,则曲线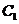 与
与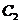 交点的极坐标为
.
交点的极坐标为
.
[标准答案]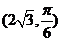 。
。
[试题解析]我们通过联立解方程组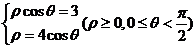 解得
解得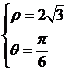 ,即两曲线的交点为
,即两曲线的交点为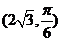 。
。
[高考考点]极坐标、极坐标方程.
22.C(本小题满分10分)选修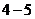 ;不等式选讲
;不等式选讲
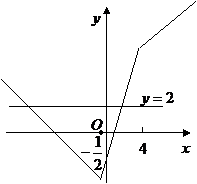 设函数
设函数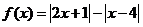 .
.
(I)解不等式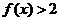 ;
;
(II)求函数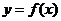 的最小值.
的最小值.
解:
(Ⅰ)令 ,则
,则
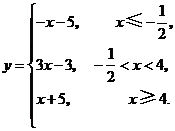 ...............3分
...............3分
作出函数 的图象,它与直线
的图象,它与直线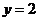 的交点为
的交点为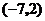 和
和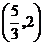 .
.
所以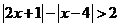 的解集为
的解集为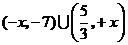 .
.
(Ⅱ)由函数 的图像可知,当
的图像可知,当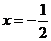 时,
时, 取得最小值
取得最小值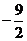 .
.
22.B(本小题满分10分)选修4-4:坐标系与参数方程
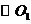 和
和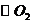 的极坐标方程分别为
的极坐标方程分别为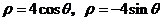 .
.
(Ⅰ)把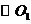 和
和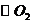 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(Ⅱ)求经过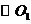 ,
,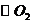 交点的直线的直角坐标方程.
交点的直线的直角坐标方程.
解:以极点为原点,极轴为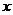 轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
轴正半轴,建立平面直角坐标系,两坐标系中取相同的长度单位.
(Ⅰ) ,
,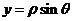 ,由
,由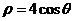 得
得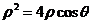 .
.
所以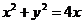 .
.
即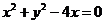 为
为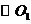 的直角坐标方程.
的直角坐标方程.
同理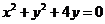 为
为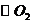 的直角坐标方程.
的直角坐标方程.
(Ⅱ)由
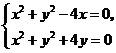 解得
解得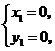
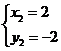 .
.
即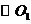 ,
,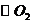 交于点
交于点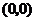 和
和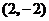 .过交点的直线的直角坐标方程为
.过交点的直线的直角坐标方程为 .
.
22.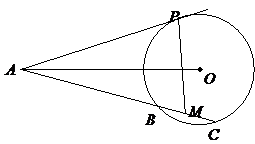 A(本小题满分10分)选修4-1:几何证明选讲
A(本小题满分10分)选修4-1:几何证明选讲
如图,已知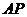 是
是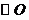 的切线,
的切线, 为切点,
为切点,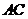 是
是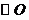 的割线,与
的割线,与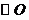 交于
交于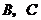 两点,圆心
两点,圆心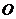 在
在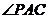 的内部,点
的内部,点 是
是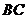 的中点.
的中点.
(Ⅰ)证明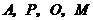 四点共圆;
四点共圆;
(Ⅱ)求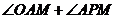 的大小.
的大小.
(Ⅰ)证明:连结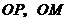 .
.
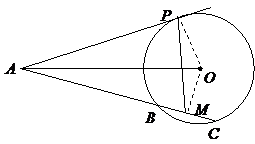 因为
因为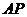 与
与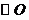 相切于点
相切于点 ,所以
,所以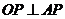 .
.
因为 是
是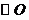 的弦
的弦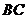 的中点,所以
的中点,所以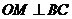 .
.
于是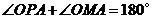 .
.
由圆心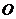 在
在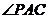 的内部,可知四边形
的内部,可知四边形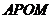 的对角互补,所以
的对角互补,所以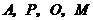 四点共圆.
四点共圆.
(Ⅱ)解:由(Ⅰ)得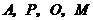 四点共圆,所以
四点共圆,所以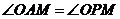 .
.
由(Ⅰ)得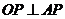 .
.
由圆心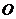 在
在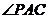 的内部,可知
的内部,可知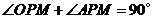 .
.
所以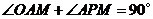

22.请考生在 三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
三题中任选一题作答,如果多做,则按所做的第一题记分.作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑.
14.(坐标系与参数方程选做题)在极坐标系中,直线l的方程为ρsinθ=3,则点(2,π/6)到直线l的距离为
.
[解析]法1:画出极坐标系易得答案2; 法2:化成直角方程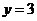 及直角坐标
及直角坐标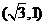 可得答案2.
可得答案2.
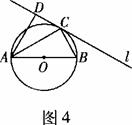 15.(几何证明选讲选做题)如图4所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D, 则∠DAC=
.
15.(几何证明选讲选做题)如图4所示,圆O的直径AB=6,C为圆周上一点,BC=3过C作圆的切线l,过A作l的垂线AD,垂足为D, 则∠DAC=
.
[解析]由某定理可知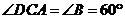 ,又
,又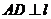 ,
,
故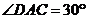 .
.

(2007海南、宁夏)
15.几何证明选讲选做题]如图所示,圆O的直径为6,C为圆周上一点。BC=3,过C作圆的切线l,过A作l的垂线AD,垂足为D,则∠DAC=______;线段AE的长为_______。
答案: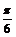 ;3。
;3。
解析:根据弦切角等于夹弧所对的圆周角及直角三角形两锐角互余,很容易得到答案; AE=EC=BC=3;
(2007广东文)
14.(不等式选讲选做题)设函数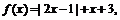 则
则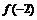 =_____;若
=_____;若 ,则x的取值范围是________;
,则x的取值范围是________;
 答案:6;
答案:6;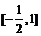

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com