
7.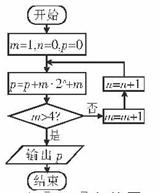 如右图程序框图,若输出
如右图程序框图,若输出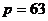 ,则输入框应填入
,则输入框应填入
A.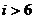 B.
B.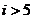
C.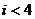 D.
D.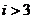
6.若变量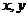 满足约束条件
满足约束条件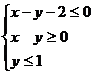 ,则目标函数
,则目标函数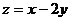 的最大值为 ( )
的最大值为 ( )
A.-3 B.3 C.-1 D.1
5.已知等比数列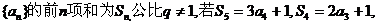 则q等于
则q等于
( )
A.2 B.-2 C.3 D.-1
4.命题“对任意直线l,有平面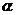 与其垂直”的否定是 ( )
与其垂直”的否定是 ( )
A.对任意直线l,没有平面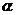 与其垂直
与其垂直
B.对任意直线l,没有平面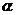 与其不垂直
与其不垂直
C.存在直线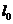 ,有平面
,有平面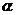 与其不垂直
与其不垂直
D.存在直线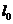 ,没有平面
,没有平面 与其不垂直
与其不垂直
3.将一个总体为A,B,C三层后,其个体数之比为4:2:1,若用分层抽样的方法抽取容量为140的样本,则应从B层中抽取的个体数为 ( )
A.20 B.30 C.40 D.60
2.设复数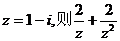 等于 ( )
等于 ( )
A.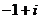 B.
B.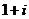 C.
C.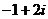 D.
D.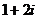
1.已知全集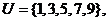 集合A={1,5,7},B={3,5,7},则
集合A={1,5,7},B={3,5,7},则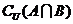 等于( )
等于( )
A.{3,7,9} B.{1,3,9} C.{1,3} D.{3,9}
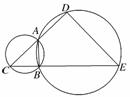
8.如图,A、B是两圆的交点,AC是小圆的直径,D和E
分别是CA和CB的延长线与大圆的交点,已知AC=4,
BE=10,且BC=AD,求DE的长.
解:设CB=AD=x,则由割线定理,得CA·CD=CB·CE,
即4(4+x)=x(x+10),化简得x2+6x-16=0,解得x=2或x=-8(舍去),即CD=6,CE=12,因为CA为直径,所以∠CBA=90°,即∠ABE=90°,则由圆的内接四边形对角互补,得∠D=90°,则CD2+DE2=CE2,∴62+DE2=122,
∴DE=6.
7.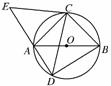 如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中
如图,△ABC是圆O的内接三角形,AC=BC,D为圆O中
 上一点,延长DA至点E,使得CE=CD.
上一点,延长DA至点E,使得CE=CD.
(1)求证:AE=BD;
(2)若AC⊥BC,求证:AD+BD=CD.
证明:(1)在△ABC中,∠CAB=∠CBA.
在△ECD中,∠CED=∠CDE.
∵∠CBA=∠CDE,∴∠ACB=∠ECD.
∴∠ACB-∠ACD=∠ECD-∠ACD.
∴∠ACE=∠BCD.
又CE=CD,AC=BC,
∴△ACE≌△BCD.
∴AE=BD.
(2)若AC⊥BC,
∵∠ACB=∠ECD,
∴∠ECD=90°,∠CED=∠CDE=45°.
∴DE=CD.
又∵AD+BD=AD+EA=ED,
 ∴AD+BD=CD.
∴AD+BD=CD.
6.如图,AB、CD是圆的两条平行弦,BE∥AC,并交CD
于E,交圆于F,过A点的切线交DC的延长线于P,
PC=ED=1,PA=2.
(1)求AC的长;
(2)求证:EF=BE.
解:(1)∵PA2=PC·PD,PA=2,PC=1,∴PD=4,
又∵PC=ED=1,∴CE=2.
∵∠PAC=∠CBA,∠PCA=∠CAB,
∴△PAC∽△CBA,
∴=,∴AC2=PC·AB,
又∵AB∥CE,AC∥BE,
∴四边形ABEC为平行四边形,
∴AB=CE=2,∴AC=.
(2)证明:∵CE·ED=BE·EF,BE=AC=.
∴EF==,∴EF=BE.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com