
8.已知下列四个命题:①若f(x)为减函数,则-f(x)为增函数;②若f(x)为增函数,则函数g(x)=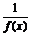 在其定义域内为减函数;③若f(x)与g(x)均为(a,b)上的增函数,则f(x)·g(x)也是区间(a,b)上的增函数;④若f(x)与g(x)在(a,b)上分别是递增与递减函数,且g(x)≠0,则
在其定义域内为减函数;③若f(x)与g(x)均为(a,b)上的增函数,则f(x)·g(x)也是区间(a,b)上的增函数;④若f(x)与g(x)在(a,b)上分别是递增与递减函数,且g(x)≠0,则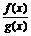 在(a,b)上是递增函数.其中正确命题的序号是
.
在(a,b)上是递增函数.其中正确命题的序号是
.
答案 ①
7.已知y=f(x)是定义在(-2,2)上的增函数,若f(m-1)<f(1-2m),则m的取值范围是 .
答案 (-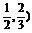
6.设f(x)=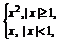 g(x)是二次函数.若f(g(x))的值域是[0,+∞),则g(x)的值域是
( )
g(x)是二次函数.若f(g(x))的值域是[0,+∞),则g(x)的值域是
( )
?A.(-∞,-1]∪[1,+∞)? B.(-∞,-1]∪[0,+∞)
?C.[0,+∞) D.[1,+∞)
答案?C?
5.已知f(x)=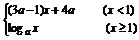 是(-∞,+∞)上的减函数,那么a的取值范围是 ( )
是(-∞,+∞)上的减函数,那么a的取值范围是 ( )
?A.(0,1)
B.(0,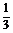 )
)
?C.[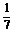 ,
,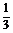 )?
D.[
)?
D.[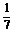 ,1)
,1)
答案?C?
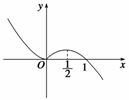
4.函数f(x)(x∈R)的图象如图所示,则函数g(x)=f(logax) (0<a<1)的单调减区间是
(
) 
?A.[0,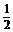 ]
B.(-∞,0)∪[
]
B.(-∞,0)∪[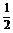 ,+∞)
,+∞)
?C.[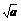 ,1]
D.[
,1]
D.[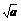 ,
,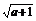 ]
]
答案?C?
3.函数y=lg(x2+2x+m)的值域是R,则m的取值范围是 ( )
?A.m>1? B.m≥1 C.m≤1? D.m∈R
答案?C?
2.已知函数f(x)在区间[a,b]上单调,且f(a)·f(b)<0,则方程f(x)=0在区间[a,b]上
( )
?A.至少有一实根 B.至多有一实根
?C.没有实根? D.必有惟一的实根
答案?D?
1.函数f(x)=ln(4+3x-x2)的单调递减区间是 ( )
? A.(-∞,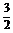 ] ?B.[
] ?B.[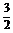 ,+∞) C.(-1,
,+∞) C.(-1,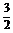 ]? D.[
]? D.[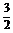 ,4)
,4)
答案?D?
4.已知定义在区间(0,+∞)上的函数f(x)满足f(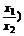 =f(x1)-f(x2),且当x>1时,f(x)<0.
=f(x1)-f(x2),且当x>1时,f(x)<0.
(1)求f(1)的值;
(2)判断f(x)的单调性;
(3)若f(3)=-1,解不等式f(|x|)<-2.
解 (1)令x1=x2>0,
代入得f(1)=f(x1)-f(x1)=0,故f(1)=0.
(2)任取x1,x2∈(0,+∞),且x1>x2,则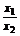 >1,
>1,
由于当x>1时,f(x)<0,
所以f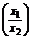 <0,即f(x1)-f(x2)<0,
<0,即f(x1)-f(x2)<0,
因此f(x1)<f(x2),
所以函数f(x)在区间(0,+∞)上是单调递减函数.
(3)由f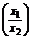 =f(x1)-f(x2)得
=f(x1)-f(x2)得
f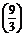 =f(9)-f(3),而f(3)=-1,所以f(9)=-2.
=f(9)-f(3),而f(3)=-1,所以f(9)=-2.
由于函数f(x)在区间(0,+∞)上是单调递减函数,
由f(|x|)<f(9),得|x|>9,∴x>9或x<-9.因此不等式的解集为{x|x>9或x<-9}.

3.在经济学中,函数f(x)的边际函数Mf(x)定义为Mf(x)=f(x+1)-f(x).某公司每月最多生产100台报警系统装置,生产x(x>0)台的收入函数为R(x)=3 000x-20x2 (单位:元),其成本函数为C(x)=500x+4 000(单位:元),利润是收入与成本之差.
(1)求利润函数P(x)及边际利润函数MP(x);
(2)利润函数P(x)与边际利润函数MP(x)是否具有相同的最大值?
解 (1)P(x)=R(x)-C(x)=(3 000x-20x2)-(500x+4 000)=-20x2+2 500x-4 000(x∈[1,100]且x∈N)
MP(x)=P(x+1)-P(x)=-20(x+1)2+2 500(x+1)-4 000-(-20x2+2 500x-4 000)
=2 480-40x (x∈[1,100]且x∈N).
(2)P(x)=-20(x-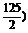 2+74 125,当x=62或63时,P(x)max=74 120(元).
2+74 125,当x=62或63时,P(x)max=74 120(元).
因为MP(x)=2 480-40x是减函数,所以当x=1时,MP(x)max=2 440(元).
因此,利润函数P(x)与边际利润函数MP(x)不具有相同的最大值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com