
7.(理)在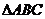 中,已知
中,已知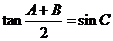 ,给出以下4个论断:
,给出以下4个论断:
(1) (2)
(2)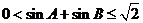 (3)
(3)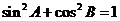
(4)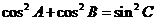 其中正确的是
其中正确的是
A.(1)(3) B.(2)(4) C.(1)(4) D.(2)(3)
(文)在等差数列{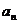 }中,若
}中,若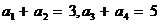 ,则
,则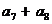 的值为 ( )
的值为 ( )
A.7 B.8 C.9 D.10
6.与双曲线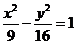 有共同的渐近线,且经过点
有共同的渐近线,且经过点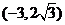 的双曲线方程为 ( )
的双曲线方程为 ( )
A.
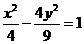 B.
B.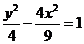 C.
C.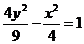 D.
D.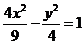
5.(理)化简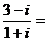 ( )
( )
A.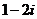 B.
B.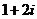 C.
C.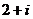 D.
D.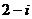
(文)已知P为抛物线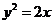 上的动点,点P的纵坐标是4,则点P到准线的距离是( )
上的动点,点P的纵坐标是4,则点P到准线的距离是( )
 A.
A.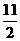 B.
B.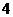 C.
C.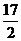 D.5
D.5
4.已知函数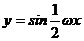 在
在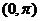 内是减函数,则 ( )
内是减函数,则 ( )
A.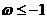 B.
B.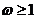 C.
C.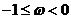 D.
D.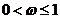
3.(理)函数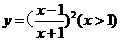 的反函数是 ( )
的反函数是 ( )
A.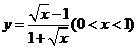 B.
B.
C.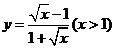 D.
D.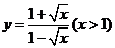
(文)函数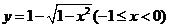 的反函数是 ( )
的反函数是 ( )
A.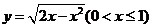 B.
B.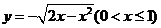
C.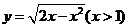 D.
D.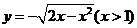
2.一正方体内接于一个球,过球心作一个截面,下面几个截面中必定错误的是 ( )
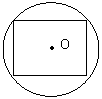
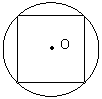

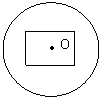
A B C D
1.函数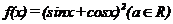 的最小正周期是 ( )
的最小正周期是 ( )
A.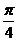 B.
B.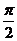 C.
C.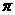 D.
D.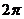
(二)
1.已知集合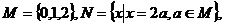 则集合
则集合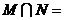 ( )
( )
A.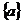 B.
B.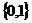 C.
C.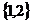 D.
D.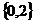
2.(文)不等式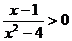 的解集是 ( )
的解集是 ( )
A.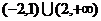 B.
B.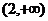 C.
C.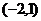 D.
D.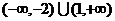
(理)设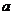 是实数,且
是实数,且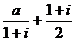 是实数,则
是实数,则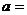 ( )
( )
A.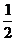 B.1 C.
B.1 C.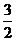 D.2
D.2
3.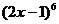 展开式中
展开式中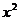 的系数为 ( )
的系数为 ( )
A.15 B.60 C.120 D.240
4.若奇函数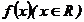 满足
满足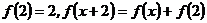 则
则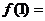 ( )
( )
A.0 B.1 C.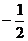 D.
D.
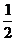
5.在(0,2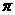 )内,使
)内,使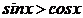 成立的
成立的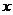 的取值范围为 ( ) A.
的取值范围为 ( ) A. B.
B.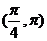
C.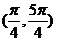 D.
D.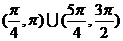
6.(文)已知等差数列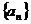 中,前
中,前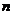 项和为
项和为 若
若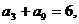 则
则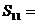 ( )
( )
A.12 B. 33 C.66 D.99
(理)在等比数列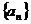 中,前
中,前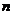 项和为
项和为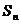 ,若
,若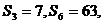 则
则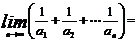
( )
A.-2 B.2 C.-3 D.3
7.对关于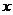 的方程
的方程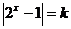 给出下列四个命题: ( )
给出下列四个命题: ( )
①存在实数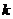 ,使得方程恰有1个零根;
,使得方程恰有1个零根;
②存在实数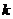 ,使得方程恰有1个正根;
,使得方程恰有1个正根;
③存在实数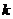 ,使得方程恰有1个正根、一个负根
,使得方程恰有1个正根、一个负根
④存在实数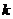 ,使得方程没有实根。
,使得方程没有实根。
其中,真命题的个数是 ( )
A.1 B.2 C.3 D.4
8.(文)直线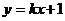 与曲线
与曲线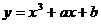 相切于点
相切于点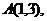 则
则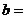 ( ) A.5 B.-5 C.3 D.-3
( ) A.5 B.-5 C.3 D.-3
(理)设随机变量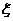 服从正态分布
服从正态分布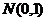 ,记
,记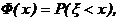 则下列结论不正确的是
则下列结论不正确的是
( ) A.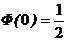 B.
B.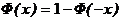
C. D.
D.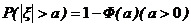
9.5人站成一排,甲、乙两人之间恰有1人的不同站法的种数为 ( )
A.18 B.24 C.36 D.48
10.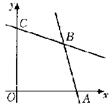 如图,目标函数
如图,目标函数 的可行域为四边形
的可行域为四边形 (含边界),
(含边界),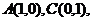 若
若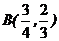 为目标函数取最大值的最优解,则
为目标函数取最大值的最优解,则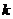 的取值范围是
的取值范围是
( )
A.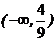 B.
B.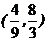
C.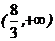 D.
D.
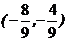
11.正三棱锥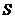 -
-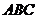 中,侧棱
中,侧棱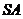 、
、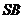 、
、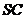 两两垂直,若底面边长为
两两垂直,若底面边长为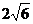 ,则此正三棱锥
,则此正三棱锥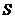 -
-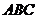 外接球的表面积是 ( )
外接球的表面积是 ( )
A.12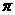 B.
B.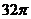 C.
C. D.
D.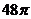
12.(文)设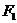 、
、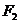 分别是椭圆
分别是椭圆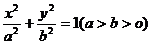 的左、右焦点,
的左、右焦点,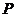 是椭圆上的一点,且
是椭圆上的一点,且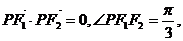 则椭圆离心率是 ( )
则椭圆离心率是 ( )
A.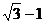 B.
B.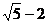 C.
C.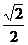 D.
D.
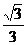
(理)设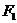 、
、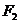 分别是椭圆
分别是椭圆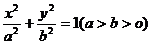 的左、右焦点,若其右准线上存在点
的左、右焦点,若其右准线上存在点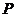 ,使线段
,使线段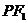 的中垂线过点
的中垂线过点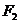 ,则椭圆离心率的取值范围是 ( )
,则椭圆离心率的取值范围是 ( )
A.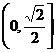 B.
B.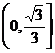 C.
C.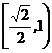 D.
D.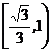
第二节 书面表达:(满分25分)
假如你是李华,今年上高三,高考在即,看到大家每天为自己所做的一切,深有感触。请根据下表提示,写一篇100字左右的短文,可增加细节,适当发挥。
|
家长 |
生活上的照顾 |
|
学校 |
提供方便(提前10分钟放学,延长图书馆的开放时间……) |
|
老师 |
学习上的帮助(鼓励,答疑解难……) |
|
你自己 |
(自由发挥,至少两点) |
郑州市第四十七中学高三第一次月考英语试题 (September 11, 2010)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com