
(一)课本P53习题7.3
10.光线从点M(-2,3)射到 轴上一点P(1,0)后被
轴上一点P(1,0)后被 轴反射,求反射光线所在的直线的方程.
轴反射,求反射光线所在的直线的方程.
解:设M′是M(-2,3)关于 轴的对称点,则M′的坐标为(-2,-3).又反射线所在直线就是过点M′、P的直线,所以反射线所在的直线方程为
轴的对称点,则M′的坐标为(-2,-3).又反射线所在直线就是过点M′、P的直线,所以反射线所在的直线方程为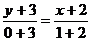 ,即:
,即: -
- -1=0.
-1=0.
11.求满足下列条件的方程:
(1)经过两条直线2 -3
-3 +10=0和3
+10=0和3 +4
+4 -2=0的交点,且垂直于直线3
-2=0的交点,且垂直于直线3 -2
-2 +4=0;
+4=0;
(2)经过两条直线2 +
+ -8=0和
-8=0和 -2
-2 +1=0的交点,且平行于直线4
+1=0的交点,且平行于直线4 -3
-3 -7=0;
-7=0;
(3)经过直线 =2
=2 +3和3
+3和3 -
- +2=0的交点,且垂直于第一条直线.
+2=0的交点,且垂直于第一条直线.
解:(1)解方程组
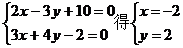
又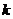 =-
=-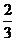 .∴
.∴ -2=-
-2=-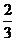 (
( +2),即2
+2),即2 +3
+3 -2=0
-2=0 
(2)解方程组
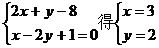
又 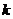 =
=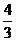 ∴
∴ -2=
-2=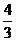 (
( -3),即4
-3),即4 -3
-3 -6=0
-6=0 
(3)解方程组
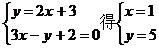
又 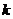 =-
=-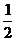 ,∴
,∴ -5=-
-5=-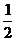 (
( -1),即
-1),即 +2
+2 -11=0.
-11=0.
12.直线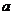
 +2
+2 +8=0,4
+8=0,4 +3
+3 =10和2
=10和2 -
- =10相交于一点,求
=10相交于一点,求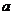 的值.
的值.
解:解方程组
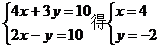
将 =4,
=4, =-2代入直线方程
=-2代入直线方程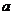
 +2
+2 +8=0得
+8=0得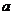 =-1
=-1 
2.判定下列各对直线的位置关系,如果相交,则求出交点的坐标.
(1) 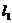 :2
:2 -
- =7 ,
=7 , :4
:4 +2
+2 =1;
=1;
(2) 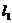 :2
:2 -6
-6 +4=0 ,
+4=0 ,  :
: =
=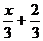 ;
;
(3) 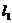 :(
:(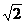 -1)
-1) +
+ =3 ,
=3 ,  :
: +(
+(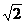 +1)
+1) =2.
=2.
解:(1)解方程组
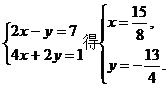 ∴两直线交点为(
∴两直线交点为(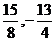 ).
).
(2) 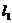 :2
:2 -6
-6 +4=0,
+4=0, :
: -3
-3 +2=0
+2=0
∵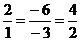 ∴两直线重合.
∴两直线重合.
(3)∵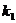 =1-
=1-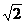 ,k2=-
,k2=-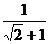 =-(
=-(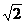 -1)=?1-
-1)=?1-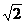 .?
.?
∴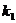 =
=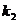 ,又
,又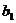 =3≠
=3≠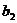 =-
=-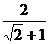 ∴
∴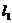 ∥
∥ .
.
解法二:解方程组
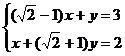
由①得 =3-(
=3-(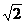 -1)
-1) 代入②得
代入②得 +(
+(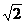 +1)(3-(
+1)(3-(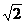 -1)
-1) )=2
)=2
整理得:3(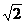 +1)=2不成立.∴方程组无解.∴直线
+1)=2不成立.∴方程组无解.∴直线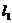 ∥
∥

课本P51练习
1.求下列各对直线的交点,并画图:
(1) 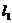 :2
:2 +3
+3 =12,
=12, :
: -2
-2 =4.
=4.
(2) 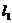 :
: =2,
=2, :3
:3 +2
+2 -12=0.
-12=0.
解:(1)解方程组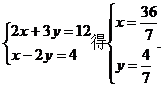 ∴交点坐标为(
∴交点坐标为(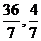 )
)
(2)解方程组
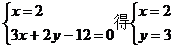 ∴交点坐标为(2,3)
∴交点坐标为(2,3)
图形依次为:
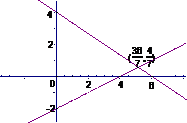
(1) (2)
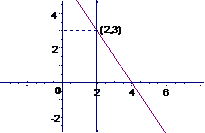
例1 当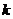 为何值时,直线
为何值时,直线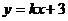 过直线
过直线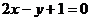 与
与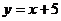 的交点?
的交点?
解法一:解方程组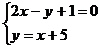 ,得交点(4,9)
,得交点(4,9)
将 =4,
=4, =9代入
=9代入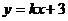 得9=4
得9=4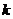 +3,解得
+3,解得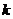 =
=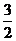 .
.
解法二:过直线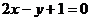 与
与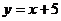 的交点的直线系方程为
的交点的直线系方程为
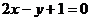 +
+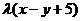 =0
=0 
整理得: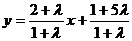 与直线
与直线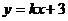 比较系数,得
比较系数,得
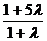 =3即
=3即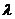 =1. ∴
=1. ∴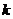 =
=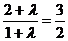

例2
已知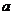 为实数,两直线
为实数,两直线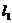 :
: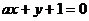 ,
, :
: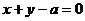 相交于一点,求证交点不可能在第一象限及
相交于一点,求证交点不可能在第一象限及 轴上.
轴上.
分析:先通过联立方程组将交点坐标解出,再判断交点横纵坐标的范围.
解:解方程组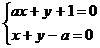 ,得交点(-
,得交点(-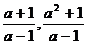 )
)
若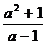 >0,则
>0,则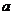 >1.当
>1.当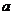 >1时,-
>1时,-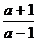 <0,此时交点在第二象限内.
<0,此时交点在第二象限内.
又因为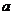 为任意实数时,都有
为任意实数时,都有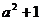
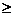 1>0,故
1>0,故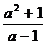 ≠0
≠0
因为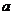 ≠1(否则两直线平行,无交点) ,所以,交点不可能在
≠1(否则两直线平行,无交点) ,所以,交点不可能在 轴上
轴上
两条直线是否相交的判断
设两条直线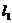 和
和 的一般式方程为
的一般式方程为
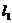 :
: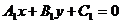 ,
, :
: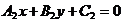

如果这两条直线相交,由于交点同时在这两条直线上,交点的坐标一定是这两个方程的惟一公共解,那么以这个解为坐标的点必是直线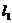 和
和 的交点.因此,两条直线是否有交点,就要看这两条直线方程所组成的方程组:
的交点.因此,两条直线是否有交点,就要看这两条直线方程所组成的方程组:
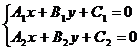 是否有惟一解
是否有惟一解
4.直线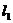 与
与 的夹角定义及公式:
的夹角定义及公式:
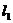 到
到 的角是
的角是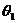 ,
,  到
到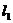 的角是π-
的角是π-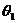 ,当
,当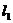 与
与 相交但不垂直时,
相交但不垂直时, 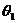 和π-
和π-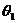 仅有一个角是锐角,我们把其中的锐角叫两条直线的夹角.
仅有一个角是锐角,我们把其中的锐角叫两条直线的夹角.
当直线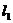 ⊥
⊥ 时,直线
时,直线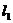 与
与 的夹角是
的夹角是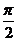 .
.
夹角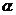 :0°<
:0°<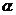 ≤90°.
≤90°.
如果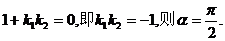
如果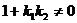 ,
,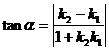

由直线方程的概念,我们知道,直线上的一点一定与二元一次方程的一组解对应,那么,如果现在有两条直线相交于一点,那么这一点与两条直线的方程又有何关系?如果我们想要在已知两直线方程的前提下求出交点,又应如何?这一交点是否与两直线方程有着一定的关系呢?
我们这一节就将研究这个问题
3.直线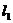 到
到 的角的定义及公式:
的角的定义及公式:
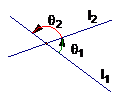 两条直线
两条直线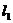 和
和 相交构成四个角,它们是两对对顶角,我们把直线
相交构成四个角,它们是两对对顶角,我们把直线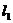 按逆时针方向旋转到与
按逆时针方向旋转到与 重合时所转的角,叫做
重合时所转的角,叫做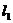 到
到 的角.
的角.
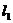 到
到 的角
的角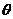 :0°<
:0°<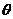 <180°,
<180°,
如果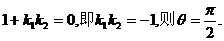
如果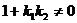 ,
,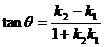

2.斜率存在时两直线的平行与垂直:
两条直线有斜率且不重合,如果它们平行,那么它们的斜率相等;反之,如果它们的斜率相等,则它们平行,即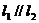
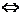
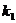 =
=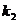 且
且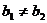
已知直线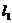 、
、 的方程为
的方程为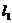 :
: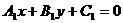 ,
,
 :
: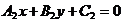
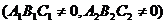
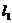 ∥
∥ 的充要条件是
的充要条件是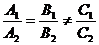

⑵两条直线垂直的情形:如果两条直线的斜率分别是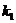 和
和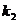 ,则这两条直线垂直的充要条件是
,则这两条直线垂直的充要条件是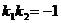 .
.
已知直线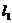 和
和 的一般式方程为
的一般式方程为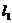 :
: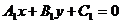 ,
,
 :
: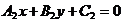 ,则
,则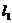
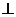

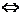
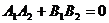 .
.
1.特殊情况下的两直线平行与垂直.
当两条直线中有一条直线没有斜率时:
(1)当另一条直线的斜率也不存在时,两直线的倾斜角都为90°,互相平行;
(2)当另一条直线的斜率为0时,一条直线的倾斜角为90°,另一条直线的倾斜角为0°,两直线互相垂直.
32. 读图2-10,回答下列问题。(20分)
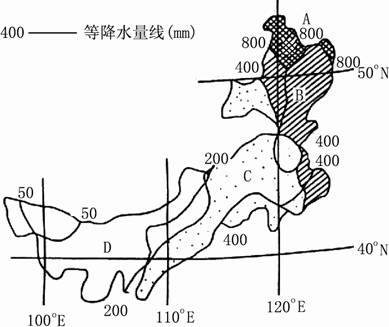
图2-10 我国某地区的干湿状况图
(1)按降水量与蒸发量的关系,可把我国划分为四类干湿区。判断A、B、C、D中属于半干旱区的是 。它与半湿润区的界线大致与400毫米年等降水量线相吻合。西北地区半干旱与干旱区的分界线是 山,此处大致与 毫米年降水量线相吻合。
(2)图中A处天然植被是 ,C处天然植被是 ,D处天然植被是 。该区植被的分布体现了 的地域分异规律,形成这种地域分异的原因是 。
(3)合理开发利用C处的土地资源的措施是 。C处这一类的土地资源主要分布在我国的 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com