
4.当0<x<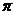 时,则方程cos (
时,则方程cos (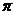 cosx)=0的解集为( )
cosx)=0的解集为( )

A. 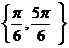 B.
B.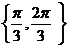 C.
C.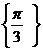 D.
D.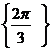


3.若sinαtgα≥0,k∈Z,则角α的集合为( )

A.[2k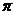 -
-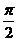 ,2k
,2k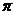 +
+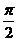 ]
B.( 2k
]
B.( 2k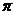 -
-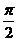 ,2k
,2k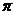 +
+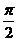 )
)

C.( 2k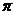 -
-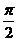 ,2k
,2k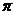 +
+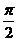 )∪
)∪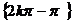 D.以上都不对
D.以上都不对

2.角α的终边与角β的终边关于y轴对称,则β为( )

A.-α B.л-α C.(2kл+1)л-α(k∈Z) D.kл-α(k∈Z)

1.已知钝角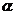 的终边经过点
的终边经过点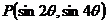 ,且
,且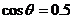 ,则
,则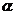 的值为 )
的值为 )

A.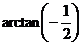 B.
B.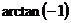 C.
C. D.
D.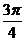


[例1] 若A、B、C是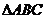 的三个内角,且
的三个内角,且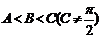 ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( )

①.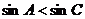 ②.
②. ③.
③.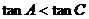 ④.
④.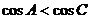


A.1
B.2
C.3
D.4

错解: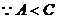 ∴
∴ 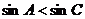 ,
,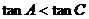 故选B
故选B

错因:三角形中大角对大边定理不熟悉,对函数单调性理解不到位导致应用错误

正解:法1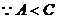 在
在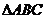 中,在大角对大边,
中,在大角对大边,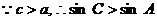


法2 考虑特殊情形,A为锐角,C为钝角,故排除B、C、D,所以选A .

[例2]已知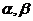 角的终边关于
角的终边关于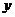 轴对称,则
轴对称,则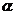 与
与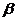 的关系为 .
的关系为 .

错解:∵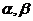 角的终边关于
角的终边关于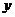 轴对称,∴
轴对称,∴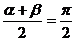 +
+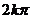 ,(
,(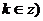


错因:把关于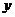 轴对称片认为关于
轴对称片认为关于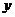 轴的正半轴对称.
轴的正半轴对称.

正解:∵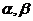 角的终边关于
角的终边关于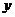 轴对称
轴对称

∴ 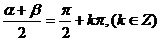 即
即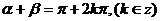


说明:(1)若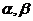 角的终边关于
角的终边关于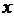 轴对称,则
轴对称,则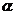 与
与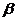 的关系为
的关系为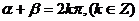


(2)若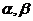 角的终边关于原点轴对称,则
角的终边关于原点轴对称,则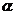 与
与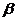 的关系为
的关系为


(3)若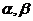 角的终边在同一条直线上,则
角的终边在同一条直线上,则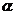 与
与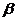 的关系为
的关系为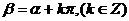


[例3] 已知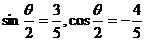 ,试确定
,试确定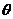 的象限.
的象限.

错解:∵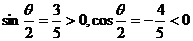 ,∴
,∴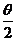 是第二象限角,即
是第二象限角,即

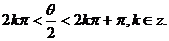


从而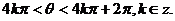


故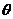 是第三象限角或第四象限角或是终边在
是第三象限角或第四象限角或是终边在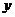 轴负半轴上的角.
轴负半轴上的角.

错因:导出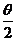 是第二象限角是正确的,由
是第二象限角是正确的,由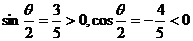 即可确定,
即可确定,

而题中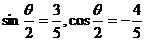 不仅给出了符号,而且给出了具体的函数值,通过其值可进一步确定
不仅给出了符号,而且给出了具体的函数值,通过其值可进一步确定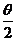 的大小,即可进一步缩小
的大小,即可进一步缩小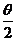 所在区间.
所在区间.

正解:∵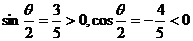 ,∴
,∴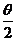 是第二象限角,
是第二象限角,

又由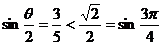 知
知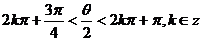


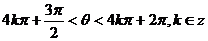 ,故
,故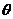 是第四象限角.
是第四象限角.

[例4]已知角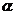 的终边经过
的终边经过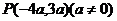 ,求
,求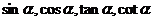 的值.
的值.

错解: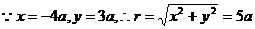


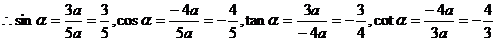


错因:在求得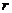 的过程中误认为
的过程中误认为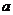
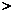 0
0

正解:若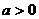 ,则
,则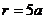 ,且角
,且角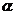 在第二象限
在第二象限

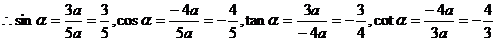


若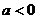 ,则
,则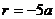 ,且角
,且角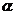 在第四象限
在第四象限

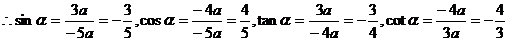


说明:(1)给出角的终边上一点的坐标,求角的某个三解函数值常用定义求解;

(2)本题由于所给字母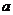 的符号不确定,故要对
的符号不确定,故要对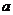 的正负进行讨论.
的正负进行讨论.

[例5] (1)已知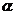 为第三象限角,则
为第三象限角,则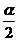 是第 象限角,
是第 象限角,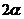 是第 象限角;
是第 象限角;

(2)若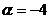 ,则
,则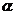 是第 象限角.
是第 象限角.

解:(1)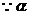 是第三象限角,即
是第三象限角,即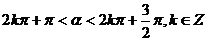


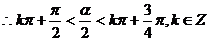 ,
,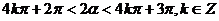


当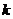 为偶数时,
为偶数时,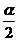 为第二象限角
为第二象限角

当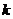 为奇数时,
为奇数时,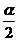 为第四象限角
为第四象限角

而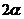 的终边落在第一、二象限或
的终边落在第一、二象限或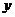 轴的非负半轴上.
轴的非负半轴上.

(2)因为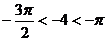 ,所以
,所以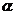 为第二象限角.
为第二象限角.

点评: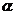 为第一、二象限角时,
为第一、二象限角时,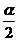 为第一、三象限角,
为第一、三象限角,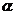 为第三、四象限角时,
为第三、四象限角时,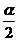 为第二、四象限角,但是它们在以象限角平分线为界的不同区域.
为第二、四象限角,但是它们在以象限角平分线为界的不同区域.

[例6]一扇形的周长为20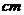 ,当扇形的圆心角
,当扇形的圆心角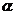 等于多少时,这个扇形的面积最大?最大面积是多少?
等于多少时,这个扇形的面积最大?最大面积是多少?

解:设扇形的半径为 ,则扇形的弧长
,则扇形的弧长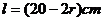


扇形的面积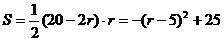


所以当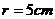 时,即
时,即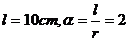 时
时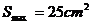 .
.

点评:涉及到最大(小)值问题时,通常先建立函数关系,再应用函数求最值的方法确定最值的条件及相应的最值.

[例7]已知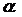 是第三象限角,化简
是第三象限角,化简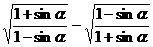 。
。

解:原式=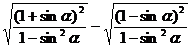 =
=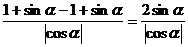


又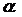 是第三象限角,
是第三象限角,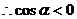


所以,原式=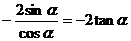 。
。

点评:三角函数化简一般要求是:(1)尽可能不含分母;(2)尽可能不含根式;(3)尽可能

使三角函数名称最少;(4)尽可能求出三角函数式的值.本题的关健是如何应用基本关系式脱去根式,进行化简.

[例8] 若角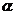 满足条件
满足条件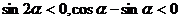 ,则
,则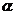 在第( )象限
在第( )象限

A.一 B.二 C.三 D.四

解: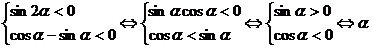 角在第二象限.故选B.
角在第二象限.故选B.

[例9] 已知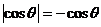 ,且
,且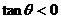 .
.

(1)试判断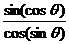 的符号;
的符号;

(2)试判断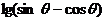 的符号.
的符号.

解:(1)由题意,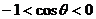 ,
,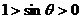


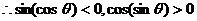 ,所以
,所以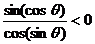 .
.

(2)由题意知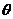 为第二象限角,
为第二象限角,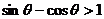 ,所以
,所以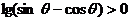 .
.

6.在计算或化简三角函数关系式时,常常需要对角的范围以及相应三角函数值的正负情况进行讨论.因此,在解答此类问题时要注意:(1)角的范围是什么?(2)对应角的三角函数值是正还是负?(3)与此相关的定义、性质或公式有哪些?

5.根据三角函数的定义可知:(1)一个角的三角函数值只与这个角的终边位置有关,即角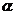 与
与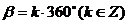 的同名三角函数值相等;(2)
的同名三角函数值相等;(2)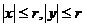 ,故有
,故有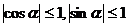 ,这是三角函数中最基本的一组不等关系.
,这是三角函数中最基本的一组不等关系.

4.确定三角函数的定义域时,主要应抓住分母为零时比值无意义这一关键.当终边在坐标轴上时点P坐标中必有一个为0.

3.在弧度的定义中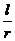 与所取圆的半径无关,仅与角的大小有关.
与所取圆的半径无关,仅与角的大小有关.

2.值得注意的几种范围角的表示法

“0 -
-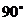 间的角”指
间的角”指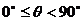 ;“第一象限角”可表示为
;“第一象限角”可表示为

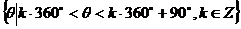 ;“小于90
;“小于90 的角”可表示为
的角”可表示为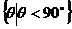 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com