
7.已知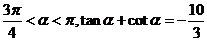
(1)求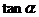 的值;
的值;
(2)求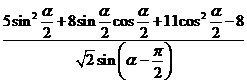 的值。
的值。
6.已知在△ABC中,sinA(sinB+cosB)-sinC=0,
sinB+cos2C=0,求角A、B、C的大小.
5.已知函数f(x)=2sinxcosx+cos2x.
(1) 求f(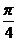 )的值; (2) 设
)的值; (2) 设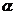 ∈(0,
∈(0,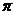 ),f(
),f(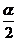 )=
)=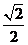 ,求sin
,求sin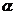 的值.
的值.
4.曲线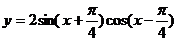 和直线
和直线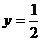 在y轴右侧的交点按横坐标从小到大依
在y轴右侧的交点按横坐标从小到大依
次记为P1,P2,P3,…,则|P2P4|等于( )
A.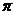 B.2
B.2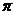 C.3
C.3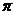 D.4
D.4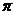
3.设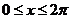 ,且
,且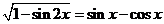 ,则
,则
A. 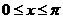 B.
B. 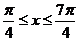 C.
C. 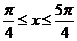 D.
D. 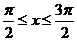
2.在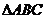 中,已知
中,已知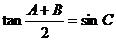 ,给出以下四个论断:
,给出以下四个论断:
① 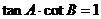 ②
② 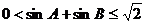
③ 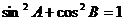 ④
④ 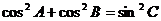
其中正确的是
A.①③ B.②④ C.①④ D.②③
1. 当0<x<л时,则方程cos (лcosx)=0的解集为( )
A. 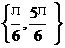 B.
B.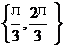 C.
C.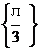 D.
D.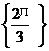
[例1]已知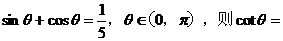 __________
__________
错解:两边同时平方,由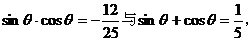 得
得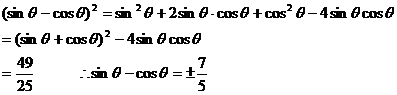
∴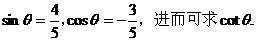 解得:
解得: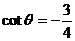
或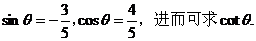 解得:
解得: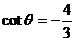
错因:没有注意到条件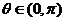 时,由于
时,由于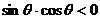
所以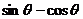 的值为正而导致错误.
的值为正而导致错误.
正解: 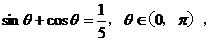
两边同时平方,有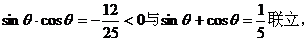
求出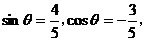 ∴
∴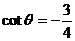
[例2]若sinA=asinB,cosA=bcosB,A、B为锐角且a>1,0<b<1,求tanA的值
错解:由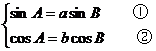 得tan A=
得tan A=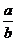 tan B
tan B
错因:对题目最终要求理解错误.不清楚最后结论用什么代数式表示
正解:由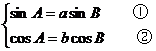 ①2+②2得a2sin2B+b2cos2B=1
①2+②2得a2sin2B+b2cos2B=1
∴cos2B=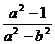 ∴sin2B=
∴sin2B=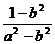 ∴tan 2B=
∴tan 2B=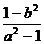
∵B为锐角
∴tan B=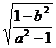
 得tan A=
得tan A=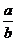 tan B=
tan B=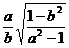
[例3]若函数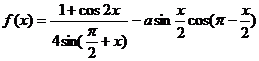 的最大值为2,试确定常数a的值.
的最大值为2,试确定常数a的值.
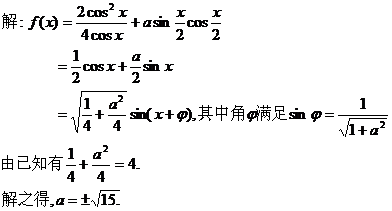
点评:本试题将三角函数“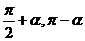 ”诱导公式有机地溶于式子中,考查了学生对基础知识的掌握程度,这就要求同学们在学习中要脚踏实地,狠抓基础.
”诱导公式有机地溶于式子中,考查了学生对基础知识的掌握程度,这就要求同学们在学习中要脚踏实地,狠抓基础.
[例4]已知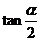 =2,求
=2,求
(1)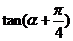 的值; (2)
的值; (2)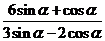 的值.
的值.
解:(1)∵ tan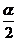 =2, ∴
=2, ∴ 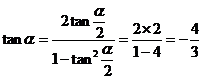 ;
;
所以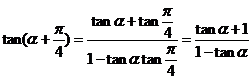 =
=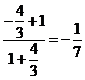 ;
;
(2)由(I), tanα=-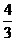 , 所以
, 所以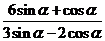 =
=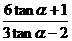 =
=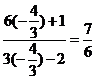 .
.
点评:本题设计简洁明了,入手容易,但对两角和与差的三角函数、同角间的基本关系式要求熟练应用,运算准确.
[例5]化简: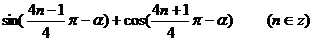
错解:原式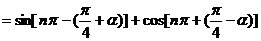
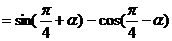
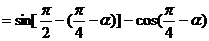

错因:对三角函数诱导公式不完全理解,不加讨论而导致错误.
正解:原式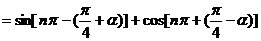
(1)当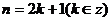 ,时
,时
原式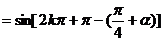 +
+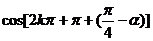
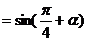
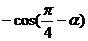
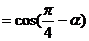
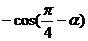 =0
=0
(2)当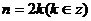 ,时
,时
原式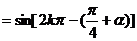 +
+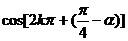
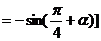 +
+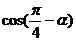 =0
=0
[例6]若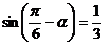 ,则
,则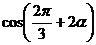 =( )
=( )
A.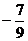 B.
B.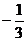 C.
C.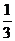 D.
D.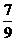
错解: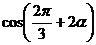 =
=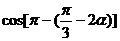 =
=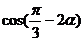 =1-2
=1-2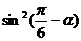 =
=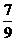
错因:诱导公式应用符号错.
正解: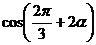 =
=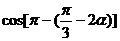
=-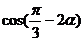 =-1+2
=-1+2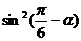 =-
=-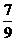 .故选A.
.故选A.
[例7].已知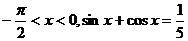 .
.
(1)求sinx-cosx的值;
(2)求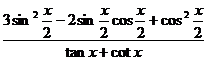 的值.
的值.
解法一:(1)由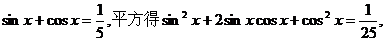
即 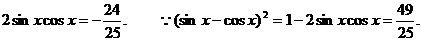
又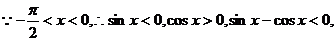 故
故 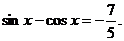
(2)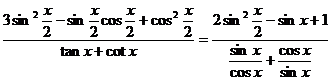
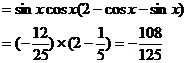
|
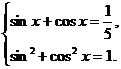
由①得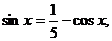 将其代入②,整理得
将其代入②,整理得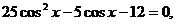
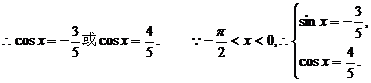
故 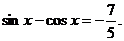
(2)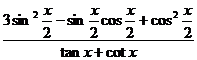
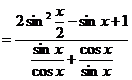
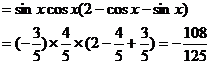
点评:本小题主要考查三角函数的基本公式、三角恒等变换、三角函数在各象限符号等基本知识,以及推理和运算能力.
[例8] (1)化简: +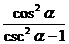 +cos2αcsc2α
+cos2αcsc2α
(2)设sin(α+)=-,且sin2α>0
求sinα,tanα
解:原式=+ +cos2αcsc2α
=cos2α+sin2α+cos2αcsc2α
=1+cot2α
=csc2α
(2)解:由sin(α+ )=- ∴cosα=- ∵sin2α>0∴2kπ<2α<2kπ+π
kπ<α<kπ+ (k∈z) ∴α为第一象限或第二象限的角
∵cosα=- <0 ∴α为第三角限角
sinα=-= tan α= =
点评:本题要求同学们熟练掌握同角三角函数之间的关系,在求值过程中特别注意三角函数值的符号的探讨.
点评:有部分同学可能会认为不等式组(*)两者没有公共部分,所以定义域为空集,原因是没有正确理解弧度与实数的关系,总认为二者格格不入,事实上弧度也是实数.
[例9]
已知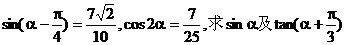 .
.
解法一:由题设条件,应用两角差的正弦公式得
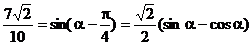
即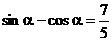 ①
①
由题设条件,应用二倍角余弦公式得
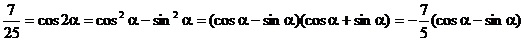 故
故 ②
②
由①式和②式得 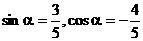 .因此,
.因此,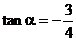 ,由两角和的正切公式
,由两角和的正切公式
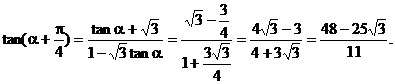
解法二:由题设条件,应用二倍角余弦公式得
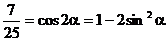 解得
解得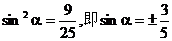
由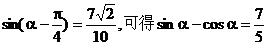
由于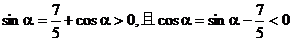 ,
,
故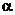 在第二象限,于是
在第二象限,于是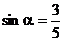 .
.
从而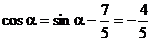 (以下同解法一).
(以下同解法一).
点评: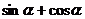 ,
,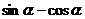 ,
,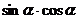 三个式子,据方程思想知一可求其二(因为其间隐含着平方关系式
三个式子,据方程思想知一可求其二(因为其间隐含着平方关系式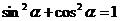 ),在求值过程中要注意符号的讨论.
),在求值过程中要注意符号的讨论.
3.已知角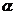 的某个三角函数值,求角
的某个三角函数值,求角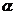 的其余5种三角函数值时,要注意公式的合理选择.在利用同角公式中的平方关系并要开方时,要根据角的范围来确定符号,常要对角的范围进行讨论.解决此类问题时,要细心求证角的范围.
的其余5种三角函数值时,要注意公式的合理选择.在利用同角公式中的平方关系并要开方时,要根据角的范围来确定符号,常要对角的范围进行讨论.解决此类问题时,要细心求证角的范围.
2.在进行三角函数化简和三角等式证明时,细心观察题目的特征,灵活恰当地选用公式,一般思路是将切割化弦.尽量化同名,同次,同角;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com