
7.设A、B、C及A1、B1、C1分别是异面直线l1、l2上的三点,而M、N、P、Q分别是线段AA1、BA1、BB1、CC1的中点.求证:M、N、P、Q四点共面.

证明: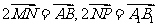 ,
,
A、B、C及A1、B1、C1分别共线,
∴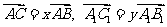
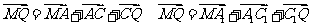
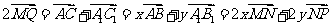
∴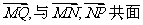 、 ∴M、N、P、Q四点共面.
、 ∴M、N、P、Q四点共面.
6. A是△BCD所在平面外一点,M、N分别是△ABC和△ACD的重心,若BD=4,则MN的长为 .
答案:
1-3, ACC; 4. 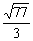 ; 5. a=16
; 5. a=16 6.
6. 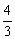
[解答题]
5. 设点C(2a+1,a+1,2)在点P(2,0,0)、A(1,-3,2)、B(8,-1,4)确定的平面上,a的值等于 ;
4.已知点A(1,2,1)、B(-1,3,4)、D(1,1,1),若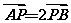 ,则|
,则|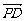 |的值是__________.
|的值是__________.
3.下列命题中不正确的命题个数是
①若A、B、C、D是空间任意四点,则有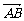 +
+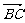 +
+ 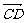 +
+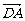 =0 ②|a|-|b|=|a+b|是a、b共线的充要条件
=0 ②|a|-|b|=|a+b|是a、b共线的充要条件
③若a、b共线,则a与b所在直线平行
④对空间任意点O与不共线的三点A、B、C,若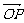 =x
=x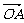 +y
+y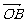 +z
+z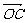 (其中x、y、z∈R),则P、A、B、C四点共面 ( )
(其中x、y、z∈R),则P、A、B、C四点共面 ( )
A.1 B.2 C.3 D.4
[填空题]
2.在空间直角坐标系中,已知点P(x,y,z),下列叙述中正确的个数是 ( )
①点P关于x轴对称点的坐标是P1(x,-y,z)
②点P关于yOz平面对称点的坐标是P2(x,-y,-z)
③点P关于y轴对称点的坐标是P3(x,-y,z)
④点P关于原点对称的点的坐标是P4(-x,-y,-z)
A.3 B.2 C.1 D.0
1.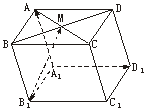 平行六面体ABCD-A1B1C1D1中,M为AC和BD的交点,若
平行六面体ABCD-A1B1C1D1中,M为AC和BD的交点,若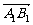 =a,
=a,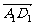 =b,
=b,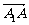 =c,则下列式子中与
=c,则下列式子中与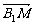 相等的是 ( )
相等的是 ( )
A.-
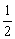 a+
a+ 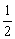 b+c B.
b+c B. 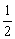 a+
a+ 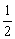 b+c
b+c
C. 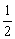 a-
a- 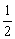 b+c D.-
b+c D.-
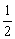 a-
a- 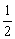 b+c
b+c
2.要熟练掌握空间向量平行、垂直的条件及三个向量共面及四点共面的条件,掌握运用向量判定平行、垂直和求空间直线所成的角的方法.
同步练习 9.7空间向量
[选择题]
1.在处理立体几何中的平行、垂直或求两异面直线所成的角时,用向量来解决思维简单,是模式化了的方法,是行之有效的方法.
2.用向量研究研究问题可以建立坐标系用向量的代数形式,也可用向量的几何形式.
[例3] 已知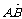 =(2,2,1),
=(2,2,1),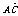 =(4,5,3),求平面ABC的单位法向量.
=(4,5,3),求平面ABC的单位法向量.
解:设面ABC的法向量n=(x,y,1),则n⊥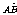 且n⊥
且n⊥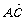 ,即n·
,即n·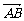 =0,且n·
=0,且n·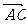 =0,即
=0,即
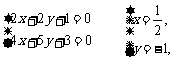
∴n=(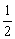 ,-1,1),单位法向量n0=±
,-1,1),单位法向量n0=±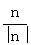 =±(
=±(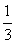 ,-
,-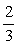 ,
,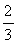 ).
).
思悟提练
求法向量一般用待定系数法.常把n的某个坐标设为1,再求另两个坐标.平面法向量是垂直于平面的向量,有方向相反的两个.
单位法向量只需将法向量再除以它的模.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com