
4、已知三种食物P、Q、R的维生素含量与成本如下表所示.
现在将xkg的食物P和ykg的食物Q及zkg的食物R混合,制成100kg的混合物.如果这100kg的混合物中至少含维生素A44 000单位与维生素B48 000单位,那么x,y,z为何值时,混合物的成本最小?
3、求直线l2:7x-y+4=0到l1:x+y-2=0的角平分线的方程。
|
|
食物P |
食物Q |
食物R |
|
维生素A(单位/kg) |
400 |
600 |
400 |
|
维生素B(单位/kg) |
800 |
200 |
400 |
|
成本(元/kg) |
6 |
5 |
4 |
2、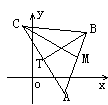 已知△ABC的顶点A(3, -1),AB边上的中线所在直线的方程为6x+10y-59=0,∠B的平分线所在直线的方程为:x-4y+10=0,求边BC所在直线的方程。
已知△ABC的顶点A(3, -1),AB边上的中线所在直线的方程为6x+10y-59=0,∠B的平分线所在直线的方程为:x-4y+10=0,求边BC所在直线的方程。
1、已知P是以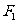 、
、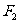 为焦点的椭圆
为焦点的椭圆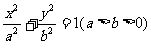 上一点,若
上一点,若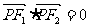
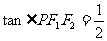 ,则椭圆的离心率为
( )
,则椭圆的离心率为
( )
(A)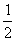 (B)
(B)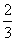 (C)
(C)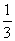 (D)
(D)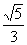
例1、(08山东高考题理科)如图,设抛物线方程为x2=2py(p>0),M为 直线y=-2p上任意一点,过M引抛物线的切线,切点分别为A,B.
(Ⅰ)求证:A,M,B三点的横坐标成等差数列;
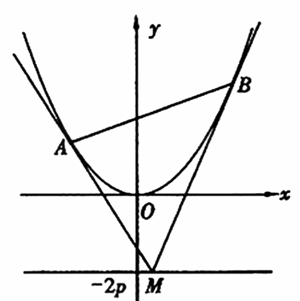 (Ⅱ)已知当M点的坐标为(2,-2p)时,
(Ⅱ)已知当M点的坐标为(2,-2p)时,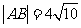 ,求此时抛物线的方程;
,求此时抛物线的方程;
(Ⅲ)是否存在点M,使得点C关于直线AB的对称点D在抛物线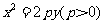 上,其中,点C满足
上,其中,点C满足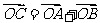 (O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(O为坐标原点).若存在,求出所有适合题意的点M的坐标;若不存在,请说明理由.
(Ⅰ)证明:由题意设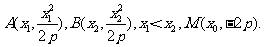
由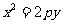 得
得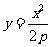 ,则
,则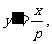
所以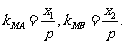
因此直线MA的方程为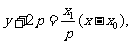
直线MB的方程为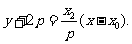
所以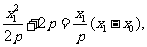 ①
①
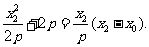 ②
②
由①、②得 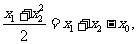
因此 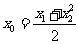 ,即
,即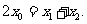
所以A、M、B三点的横坐标成等差数列.
(Ⅱ)解:由(Ⅰ)知,当x0=2时,
将其代入①、②并整理得:
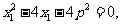
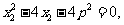
所以 x1、x2是方程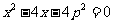 的两根,
的两根,
因此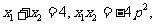
又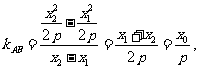
所以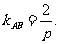
由弦长公式得

又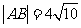 ,
,
所以p=1或p=2,
因此所求抛物线方程为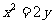 或
或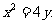
(Ⅲ)解:设D(x3,y3),由题意得C(x1+ x2, y1+ y2),
则CD的中点坐标为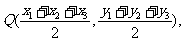
设直线AB的方程为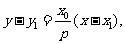
由点Q在直线AB上,并注意到点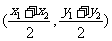 也在直线AB上,
也在直线AB上,
代入得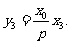
若D(x3,y3)在抛物线上,则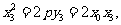
因此 x3=0或x3=2x0.
即D(0,0)或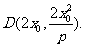
(1)当x0=0时,则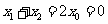 ,此时,点M(0,-2p)适合题意.
,此时,点M(0,-2p)适合题意.
(2)当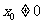 ,对于D(0,0),此时
,对于D(0,0),此时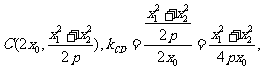
又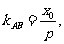 AB⊥CD,
AB⊥CD,
所以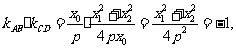
即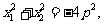 矛盾.
矛盾.
对于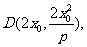 因为
因为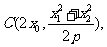 此时直线CD平行于y轴,
此时直线CD平行于y轴,
又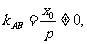
所以 直线AB与直线CD不垂直,与题设矛盾,
所以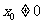 时,不存在符合题意的M点.
时,不存在符合题意的M点.
综上所述,仅存在一点M(0,-2p)适合题意.
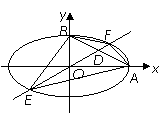
例2(08全国高考题)设椭圆中心在坐标原点,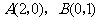 是它的两个顶点,直线
是它的两个顶点,直线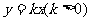 与AB相交于点D,与椭圆相交于E、F两点.
与AB相交于点D,与椭圆相交于E、F两点.
 (Ⅰ)若
(Ⅰ)若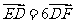 ,求
,求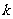 的值;
的值;
(Ⅱ)求四边形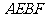 面积的最大值.
面积的最大值.
(Ⅰ)解:依题设得椭圆的方程为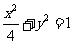 ,
,
直线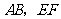 的方程分别为
的方程分别为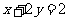 ,
,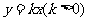 .
.
如图,设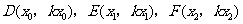 ,其中
,其中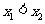 ,
,
且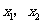 满足方程
满足方程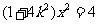 ,
,
故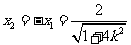 .①
.①
由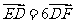 知
知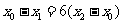 ,得
,得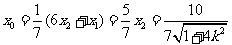 ;
;
由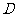 在
在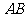 上知
上知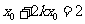 ,得
,得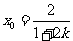 .
.
所以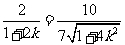 ,
,
化简得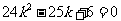 ,
,
解得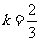 或
或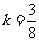 .
.
(Ⅱ)解法一:根据点到直线的距离公式和①式知,点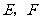 到
到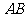 的距离分别为
的距离分别为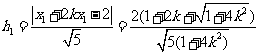 ,
,
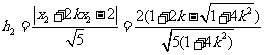 .
.
又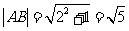 ,所以四边形
,所以四边形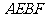 的面积为
的面积为
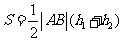
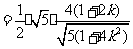
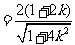
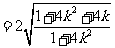
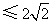 ,
,
当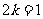 ,即当
,即当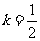 时,上式取等号.所以
时,上式取等号.所以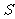 的最大值为
的最大值为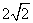 .
.
解法二:由题设,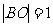 ,
,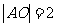 .
.
设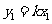 ,
,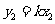 ,由①得
,由①得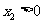 ,
,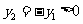 ,
,
故四边形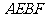 的面积为
的面积为
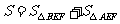
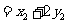
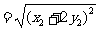
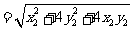
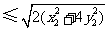
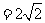 ,
,
当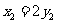 时,上式取等号.所以
时,上式取等号.所以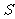 的最大值为
的最大值为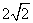 .
.
例3、已知x、y满足约束条件
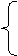 x≥1,
x≥1,
x-3y≤-4,
3x+5y≤30,
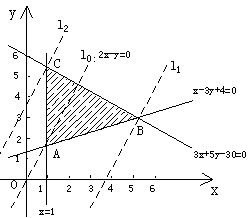 求目标函数z=2x-y的最大值和最小值.
求目标函数z=2x-y的最大值和最小值.
解:根据x、y满足的约束条件作出可行域,即如图所示的阴影部分(包括边界).
作直线 :2x-y=0,再作一组平行于
:2x-y=0,再作一组平行于 的直线
的直线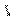 :2x-y=t,t∈R.
:2x-y=t,t∈R.
可知,当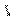 在
在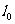 的右下方时,直线
的右下方时,直线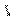 上的点(x,y)满足2x-y>0,即t>0,而且直线
上的点(x,y)满足2x-y>0,即t>0,而且直线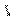 往右平移时,t随之增大.当直线
往右平移时,t随之增大.当直线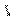 平移至
平移至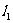 的位置时,直线经过可行域上的点B,此时所对应的t最大;当
的位置时,直线经过可行域上的点B,此时所对应的t最大;当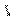 在
在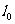 的左上方时,直线
的左上方时,直线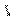 上的点(x,y)满足2x-y<0,即t<0,而且直线
上的点(x,y)满足2x-y<0,即t<0,而且直线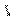 往左平移时,t随之减小.当直线
往左平移时,t随之减小.当直线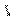 平移至
平移至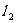 的位置时,直线经过可行域上的点C,此时所对应的t最小.
的位置时,直线经过可行域上的点C,此时所对应的t最小.
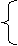 x-3y+4=0,
x-3y+4=0,
由 解得点B的坐标为(5,3);
3x+5y-30=0,
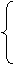 x=1,
x=1,
由
解得点C的坐标为(1,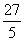 ).
).
3x+5y-30=0,
所以,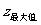 =2×5-3=7;
=2×5-3=7; =2×1-
=2×1-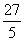 =
=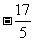 .
.
例4、(08山东高考题文科)已知曲线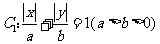 所围成的封闭图形的面积为
所围成的封闭图形的面积为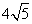 ,曲线
,曲线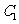 的内切圆半径为
的内切圆半径为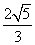 .记
.记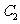 为以曲线
为以曲线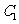 与坐标轴的交点为顶点的椭圆.
与坐标轴的交点为顶点的椭圆.
(Ⅰ)求椭圆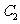 的标准方程;
的标准方程;
(Ⅱ)设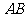 是过椭圆
是过椭圆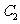 中心的任意弦,
中心的任意弦,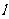 是线段
是线段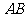 的垂直平分线.
的垂直平分线.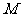 是
是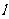 上异于椭圆中心的点.
上异于椭圆中心的点.
(1)若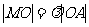 (
(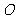 为坐标原点),当点
为坐标原点),当点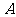 在椭圆
在椭圆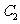 上运动时,求点
上运动时,求点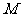 的轨迹方程;
的轨迹方程;
(2)若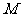 是
是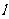 与椭圆
与椭圆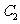 的交点,求
的交点,求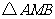 的面积的最小值.
的面积的最小值.
解:(Ⅰ)由题意得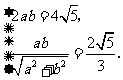
又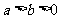 ,
,
解得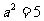 ,
,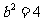 .
.
因此所求椭圆的标准方程为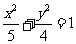 .
.
(Ⅱ)(1)假设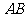 所在的直线斜率存在且不为零,设
所在的直线斜率存在且不为零,设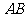 所在直线方程为
所在直线方程为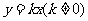 ,
,
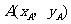 .
.
解方程组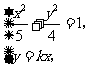 得
得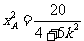 ,
,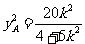 ,
,
所以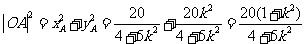 .
.
设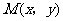 ,由题意知
,由题意知 ,
,
所以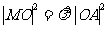 ,即
,即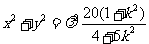 ,
,
因为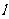 是
是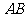 的垂直平分线,
的垂直平分线,
所以直线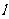 的方程为
的方程为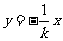 ,
,
即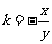 ,
,
因此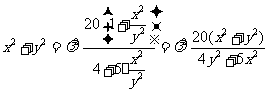 ,
,
又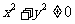 ,
,
所以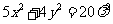 ,
,
故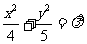 .
.
又当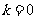 或不存在时,上式仍然成立.
或不存在时,上式仍然成立.
综上所述,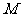 的轨迹方程为
的轨迹方程为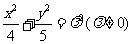 .
.
(2)当 存在且
存在且 时,由(1)得
时,由(1)得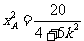 ,
,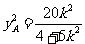 ,
,
由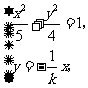 解得
解得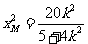 ,
,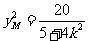 ,
,
所以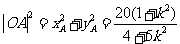 ,
,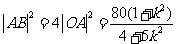 ,
,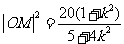 .
.
解法一:由于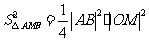
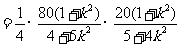
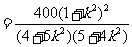
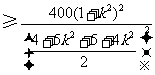
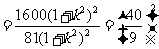 ,
,
当且仅当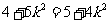 时等号成立,即
时等号成立,即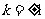 时等号成立,此时
时等号成立,此时 面积的最小值是
面积的最小值是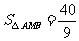 .
.
当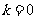 ,
,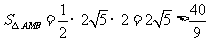 .
.
当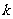 不存在时,
不存在时,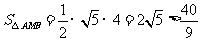 .
.
综上所述,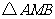 的面积的最小值为
的面积的最小值为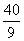 .
.
解法二:因为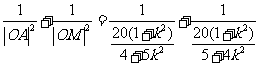
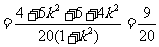 ,
,
又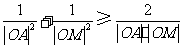 ,
,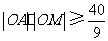 ,
,
当且仅当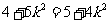 时等号成立,即
时等号成立,即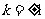 时等号成立,
时等号成立,
此时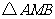 面积的最小值是
面积的最小值是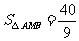 .
.
当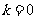 ,
,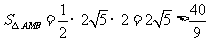 .
.
当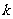 不存在时,
不存在时,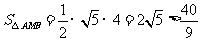 .
.
综上所述,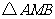 的面积的最小值为
的面积的最小值为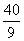 .
.
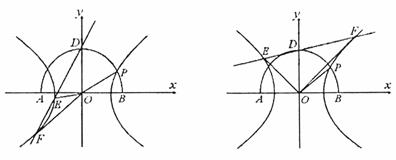
例5(08湖北高考题)如图,在以点O为圆心,|AB|=4为直径的半圆ADB中,OD⊥AB,P是半圆弧上一点,∠POB=30°,曲线C是满足||MA|-|MB||为定值的动点M的轨迹,且曲线C过点P.
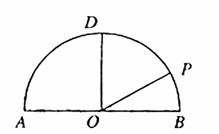
(Ⅰ)建立适当的平面直角坐标系,求曲线C的方程;
(Ⅱ)设过点D的直线l与曲线C相交于不同的两点E、F.
若△OEF的面积不小于2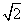 ,求直线l斜率的取值范围.
,求直线l斜率的取值范围.
解:本小题主要考查直线、圆和双曲线等平面解析几何的基础知识,考查轨迹方程的求法、不等式的解法以及综合解题能力.
(Ⅰ)解法1:以O为原点,AB、OD所在直线分别为x轴、y轴,建立平面直角坐标系,则A(-2,0),B(2,0),D(0,2),P(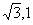 ),依题意得
),依题意得
||MA|-|MB||=|PA|-|PB|=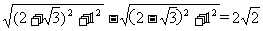 <
<
|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设实半轴长为a,虚半轴长为b,半焦距为c,
则c=2,2a=2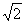 ,∴a2=2,b2=c2-a2=2.
,∴a2=2,b2=c2-a2=2.
∴曲线C的方程为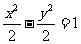 .
.
解法2:同解法1建立平面直角坐标系,则依题意可得
||MA|-|MB||=|PA|-|PB|<|AB|=4.
∴曲线C是以原点为中心,A、B为焦点的双曲线.
设双曲线的方程为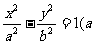 >0,b>0).
>0,b>0).
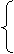 则由
则由 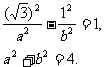 解得a2=b2=2,
解得a2=b2=2,
∴曲线C的方程为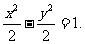
(Ⅱ)解法1:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理
得(1-k2)x2-4kx-6=0. ①
∵直线l与双曲线C相交于不同的两点E、F,
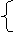
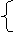 ∴
∴ 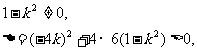
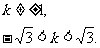
∴k∈(-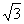 ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,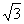 ).
②
).
②
设E(x1,y1),F(x2, y2),则由①式得x1+x2=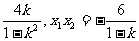 ,于是
,于是
|EF|=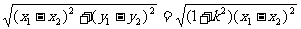
=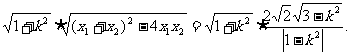
而原点O到直线l的距离d=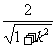 ,
,
∴S△DEF=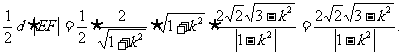
若△OEF面积不小于2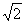 ,即S△OEF
,即S△OEF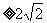 ,则有
,则有
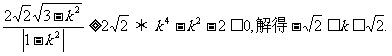 ③
③
综合②、③知,直线l的斜率的取值范围为[-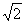 ,-1]∪(-1,1) ∪(1,
,-1]∪(-1,1) ∪(1, 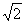 ).
).
解法2:依题意,可设直线l的方程为y=kx+2,代入双曲线C的方程并整理,
得(1-k2)x2-4kx-6=0. ①
∵直线l与双曲线C相交于不同的两点E、F,
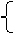
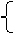 ∴
∴ 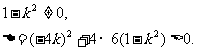
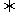
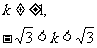 .
.
∴k∈(-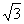 ,-1)∪(-1,1)∪(1,
,-1)∪(-1,1)∪(1,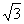 ).
②
).
②
设E(x1,y1),F(x2,y2),则由①式得
|x1-x2|=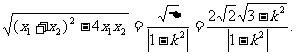 ③
③
当E、F在同一支上时(如图1所示),
S△OEF=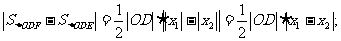
当E、F在不同支上时(如图2所示).
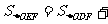 S△ODE=
S△ODE=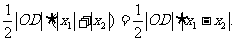
综上得S△OEF=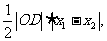 于是
于是
由|OD|=2及③式,得S△OEF=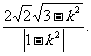
若△OEF面积不小于2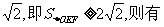
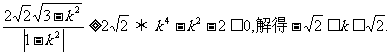 ④
④
综合②、④知,直线l的斜率的取值范围为[-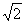 ,-1]∪(-1,1)∪(1,
,-1]∪(-1,1)∪(1,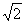 ).
).
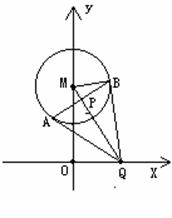
例7、 已知⊙M: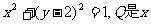 轴上的动点,QA,QB分别切⊙M于A,B两点,(1)如果
轴上的动点,QA,QB分别切⊙M于A,B两点,(1)如果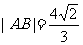 ,求直线MQ的方程;
,求直线MQ的方程;
(2)求动弦AB的中点P的轨迹方程.
解:(1)由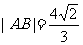 ,可得
,可得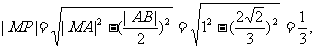 由射影定理,得
由射影定理,得 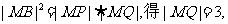 在Rt△MOQ中,
在Rt△MOQ中,
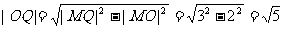 ,
,
故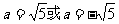 ,
,
所以直线AB方程是
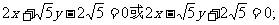
(2)连接MB,MQ,设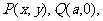 由
由
点M,P,Q在一直线上,得
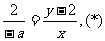 由射影定理得
由射影定理得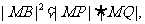
即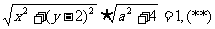 把(*)及(**)消去a,
把(*)及(**)消去a,
并注意到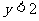 ,可得
,可得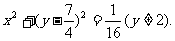
说明:适时应用平面几何知识,这是快速解答本题的要害所在。
例8、已知椭圆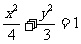 ,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1、F2距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由。
,能否在此椭圆位于y轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点F1、F2距离的等比中项,若能找到,求出该点的坐标,若不能找到,请说明理由。
解:假设存在满足条件的点,设M(x1,y1)a2=4,b2=3,∴a=2,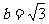 ,c=1,∴
,c=1,∴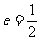 ,
,
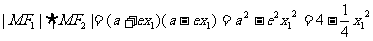 ,点M到椭圆左准线的距离
,点M到椭圆左准线的距离
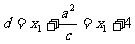 ,∴
,∴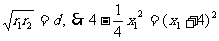 ,∴
,∴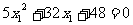 ,∴
,∴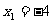 或
或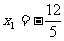 ,这与x1∈[-2,0)相矛盾,∴满足条件的点M不存在。
,这与x1∈[-2,0)相矛盾,∴满足条件的点M不存在。
例9、已知椭圆中心在原点,焦点在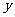 轴上,焦距为4,离心率为
轴上,焦距为4,离心率为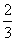 ,
,
(Ⅰ)求椭圆方程;
(Ⅱ)设椭圆在y轴正半轴上的焦点为M,又点A和点B在椭圆上,且M分有向线段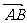 所成的比为2,求线段AB所在直线的方程。
所成的比为2,求线段AB所在直线的方程。
解:(Ⅰ)设椭圆方程为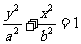 由2c=4得c=2 又
由2c=4得c=2 又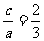
故a=3, 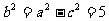 ∴所求的椭圆方程为
∴所求的椭圆方程为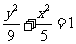
(Ⅱ)若k 不存在,则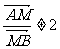 ,若k 存在,则设直线AB的方程为:y=kx+2
,若k 存在,则设直线AB的方程为:y=kx+2
又设A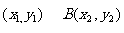
由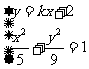 得
得 
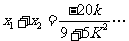 ①
①
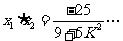 ②
②
∵点M坐标为M(0,2)
∴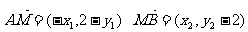
由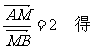
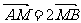 ∴
∴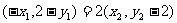
∴ 代入①、②得
代入①、②得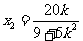 … ③
… ③
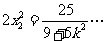 ④
④
由③、④ 得
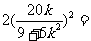
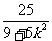 ∴
∴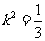
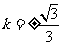
∴线段AB所在直线的方程为: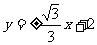 。
。
说明:有向线段所成的比,线段的定比分点等概念,本身就是解析几何研究的一类重要问题。向量概念的引入,使这类问题的解决显得简洁而流畅。求解这类问题可以用定比分点公式,也可以直接用有向线段的比解题。
另外,向量的长度,点的平移等与解析几何都有着千丝万缕的联系,向量与解析几何的结合,为解决这些问题开辟了新的解题途径。
例12、已知双曲线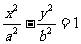 的离心率
的离心率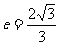 ,过
,过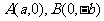 的直线到原点的距离是
的直线到原点的距离是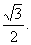
(1)求双曲线的方程;
(2)已知直线 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
解:∵(1)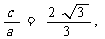 原点到直线AB:
原点到直线AB: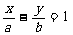 的距离
的距离 .
.
故所求双曲线方程为 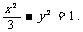
(2)把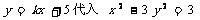 中消去y,整理得
中消去y,整理得
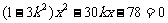 .
.
设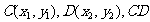 的中点是
的中点是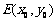 ,则
,则

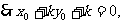
即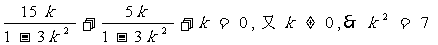
故所求k=±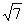 .
.
说明:为了求出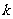 的值, 需要通过消元, 想法设法建构
的值, 需要通过消元, 想法设法建构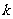 的方程.
的方程.
例15、已知椭圆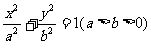 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点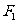 ,向量
,向量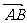 与
与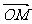 是共线向量。
是共线向量。
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点,
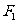 、
、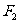 分别是左、右焦点,求∠
分别是左、右焦点,求∠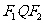 的取值范围;
的取值范围;
解:(1)∵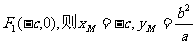 ,∴
,∴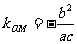 。
。
∵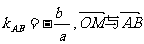 是共线向量,∴
是共线向量,∴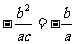 ,∴b=c,故
,∴b=c,故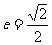 。
。
(2)设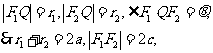
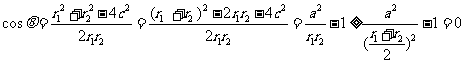
当且仅当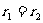 时,cosθ=0,∴θ
时,cosθ=0,∴θ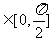 。
。
说明:由于共线向量与解析几何中平行线、三点共线等具有异曲同工的作用,因此,解析几何中与平行线、三点共线等相关的问题均可在向量共线的新情景下设计问题。求解此类问题的关键是:正确理解向量共线与解析几何中平行、三点共线等的关系,把有关向量的问题转化为解析几何问题。
例16、一条斜率为1的直线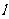 与离心率为
与离心率为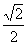 的椭圆C:
的椭圆C: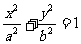 (
(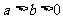 )交于P、Q,两点,直线
)交于P、Q,两点,直线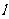 与Y轴交于点R,且
与Y轴交于点R,且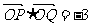 ,
,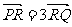 ,求直线
,求直线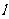 和椭圆C的方程。
和椭圆C的方程。
解: 椭圆离心率为
椭圆离心率为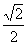 ,
,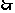
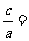
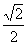 ,
,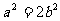
所以椭圆方程为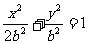 ,设
,设 方程为:
方程为: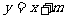 ,
,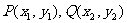
由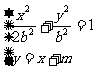 消去
消去 得
得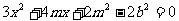
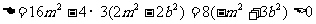
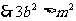
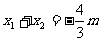 ……(1)
……(1) 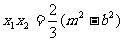 ……(2)
……(2)
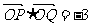 所以
所以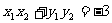
而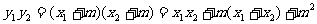
所以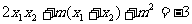
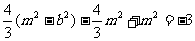
所以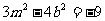 ……(3)又
……(3)又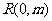 ,
,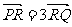 ,
,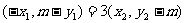 从而
从而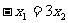 ……(4)
由(1)(2)(4)得
……(4)
由(1)(2)(4)得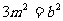 ……(5)
……(5)
由(3)(5)解得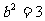 ,
,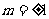 适合
适合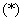 ,
,
所以所求直线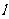 方程为:
方程为: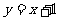 或
或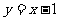 ;椭圆C的方程为
;椭圆C的方程为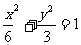
说明:向量数量积的坐标表示,构建起向量与解析几何的密切关系,使向量与解析几何融为一体。求此类问题的关键是:利用向量数量积的坐标表示,沟通向量与解析几何的联系。体现了向量的工具性。
3.命题的热点:
(1)与其他知识进行综合,在知识网络的交汇处设计试题(如与向量综合,与数列综合、与函数、导数及不等式综合等);
(2)直线与圆锥曲线的位置关系,由于该部分内容体现解析几何的基本思想方法--用代数的手段研究几何问题,因此该部分内容一直是考试的热点,相信,在09年的考试中将继续体现;
(3)求轨迹方程.
(4)应用题.
2.命题内容:从今年各地的试题以及前几年的试题来看,解答题所考查的内容基本上是椭圆、双曲线、抛物线交替出现的,所以,今年极有可能考双曲线的解答题.此外,从命题所追求的目标来看,小题所涉及的内容一定会注意到知识的覆盖,兼顾到对能力的要求.
1.难度:解析几何内容是历年来高考数学试题中能够拉开成绩差距的内容之一,该部分试题往往有一定的难度和区分度,预计这一形式仍将在09年的试题中得到体现.此外,从08年分省(市)命题的情况来看,在文科类15份试卷(含文理合用的试卷)中,有9分试卷(占3/5)用解析几何大题作为最后一道压轴题,预计这一现状很有可能在09年试卷中继续重现.
3.注意强化思维的严谨性,力求规范解题,尽可能少丢分在解解析几何的大题时,有不少学生常出现因解题不够规范而丢分的现象,因此,要通过平时的讲评对易出现错误的相关步骤作必要的强调,减少或避免无畏的丢分.
2.重视通性通法,加强解题指导,提高解题能力.在二轮复习中,不能仅仅复习概念和性质,还应该以典型的例题和习题(可以选用08年的各地高考试题和近两年的各地高考模拟试题)为载体,在二轮复习中强化各类问题的常规解法,使学生形成解决各种类型问题的操作范式.数学学习是学生自主学习的过程,解题能力只有通过学生的自主探究才能掌握.所以,在二轮复习中,教师的作用是对学生的解题方法进行引导、点拨和点评,只有这样,才能够实施有效复习.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com