4.(2001年上海，3)下列物质不属于“城市空气质量日报”报道的是

A.二氧化硫　　　　　　　　　　　　　　　　　　　　　　　 B.氮氧化物

C.二氧化碳　　　　　　　　　　　　　　　　　　　　　　　 D.悬浮颗粒

3.(2001年全国，4)为了保护臭氧层，可采取的有效措施是

A.减少二氧化硫的排放量　　　　　　　　　　　　 B.减少含铅废气的排放量

C.减少氟氯代烃的排放量　　　　　　　　　　　　 D.减少二氧化碳的排放量

2.(2002年江苏大综合，22)高温下硫酸亚铁发生如下反应：2FeSO₄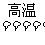Fe₂O₃+

SO₂↑+SO₃↑,若将生成的气体通入氯化钡溶液中，得到的沉淀物是

A.BaSO₃和BaSO₄ B.BaS

C.BaSO₃ D.BaSO₄

1.(2002年上海，10)水的状态除了气、液和固态外，还有玻璃态。它是由液态水急速冷却到165 K时形成的，玻璃态的水无固定形状，不存在晶体结构，且密度与普通液态水的密度相同，有关玻璃态水的叙述正确的是

A.水由液态变为玻璃态，体积缩小

B.水由液态变为玻璃态，体积膨胀

C.玻璃态是水的一种特殊状态

D.玻璃态水是分子晶体

4.设数列{a_n}的各项均为正整数，a₁=1，设S_n=a₁+a₂+……+a_n，若对自然数n总有S_n+1+S_n=( S_n+1－S_n)² ，试推测用n表示S_n的关系式(S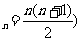

3.已知数列{a_n}中，a₁=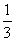, a_n+1=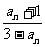求a₂,　 a₃,　 a₄，猜测通项公式a_n

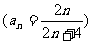
2.平面上有n条直线，其中无两条平行，无三条共点，

问：(1)这n条直线共有几个交点f(n)？(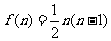

(2)这n条直线互相分割成多少条线段(或射线)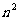？(条)

(3)平面被这n条直线分割成多少块区域？()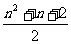

1.对一切自然数n，猜出使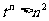成立的最小自然数t

2.首项为a₁，公比为q的等比数列的通项公式是：a_n=a₁q^n－1.

证明：(1)n=1时，左边=a₁，右边=a₁·q^1－1=a₁q⁰=a₁.

∴左边=右边.

(2)假设当n=k时等式成立.即a_k =a₁q^k－1.那么当n=k+1时.

a_k+1=a_kq=a₁q^k－1·q=a₁q^(k+1)－1

∴n=k+1时等式也成立.

由(1)、(2)可知等式对一切n∈N^*都成立

1.用数学归纳法证明：1+2+3+…+n=.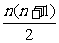

证明：(1)当n=1时，左边=1，右边=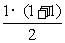=1.

∴等式成立.

(2)假设当n=k时，等式成立，即1+2+3+…+k=.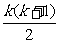

那么当n=k+1时，

1+2+3+…+k+(k+1)=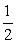k(k+1)+(k+1)=(k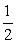+1)(k+1)=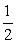(k+1)(k+1+1)

∴n=k+1时，等式也成立.

由(1)(2)可知等式对一切n∈N*都成立.