
1、对于函数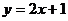 填写下表,并画出函数的图象,观察当
填写下表,并画出函数的图象,观察当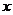 无限趋近于1时的变化趋势,说出当
无限趋近于1时的变化趋势,说出当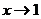 时函数
时函数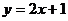 的极限
的极限
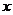 |
0.1 |
0.9 |
0.99 |
0.999 |
0.9999 |
0.99999 |
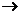 |
1 |
|
y=2X+1 |
|
|
|
|
|
|
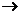 |
|
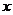 |
1.5 |
1.1 |
1.01 |
1.001 |
1.0001 |
1.00001 |
 |
1 |
|
y=2X+1 |
|
|
|
|
|
|
 |
|
求下列函数在X=0处的极限
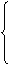 (1)
(1)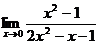 (2)
(2)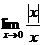 (3)
(3)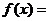
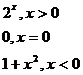
就问题(3)展开讨论:函数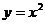 当
当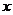 无限趋近于2时的变化趋势
无限趋近于2时的变化趋势
当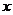 从左侧趋近于2时 (
从左侧趋近于2时 (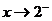 )
)
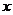 |
1.1 |
1.3 |
1.5 |
1.7 |
1.9 |
1.99 |
1.999 |
1.9999 |
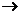 |
2 |
|
y=x2 |
1.21 |
|
|
|
|
|
|
|
 |
|
当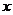 从右侧趋近于2时 (
从右侧趋近于2时 (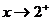 )
)
 |
2.9 |
2.7 |
2.5 |
2.3 |
2.1 |
2.01 |
2.001 |
2.0001 |
 |
2 |
|
y=x2 |
8.41. |
7.29 |
|
|
|
|
|
|
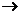 |
|
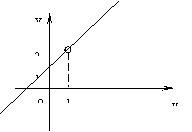 发现
发现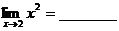
我们再继续看
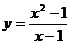
当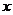 无限趋近于1(
无限趋近于1(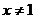 )时的变化趋势;
)时的变化趋势;
函数的极限有概念:当自变量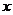 无限趋近于
无限趋近于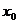 (
(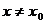 )时,如果函数
)时,如果函数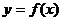 无限趋近于一个常数A,就说当
无限趋近于一个常数A,就说当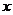 趋向
趋向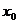 时,函数
时,函数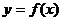 的极限是A,记作
的极限是A,记作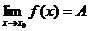 。
。
特别地,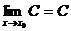 ;
;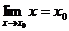
(1)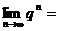 _____
_____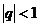 ;(2)
;(2)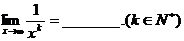
(3)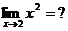
18.自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响. 用xn表示某鱼群在第n年年初的总量,n∈N*,且x1>0.不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c.
(Ⅰ)求xn+1与xn的关系式;
(Ⅱ)猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
(Ⅲ)设a=2,b=1,为保证对任意x1∈(0,2),都有xn>0,n∈N*,则捕捞强度b的最大允许值是多少?证明你的结论.
17.
讨论 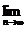
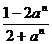 的值.
的值. 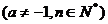
16.已知 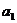 =
= ,且
,且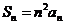
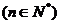
(1) 求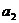 ,
,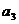 ,
,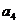
(2) 猜测{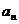 }的通项公式,并用数学归纳法证明之.
}的通项公式,并用数学归纳法证明之.
15.用数学归纳法证明: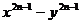 能被x -y整除.
能被x -y整除. 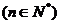
14.若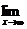
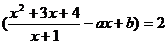 , 则a=_________,b=_________.
, 则a=_________,b=_________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com