
3. 1980年以来,黑龙江西部水稻集中种植区向北推移了一个纬度左右,替代了原玉米种植区。引起这一变化的主要自然因素是
A. 土壤肥力 B. 热量条件 C. 河流汛期 D. 降水总量
[解析]水稻生长对气候尤其是热量条件要求较高,全球气候变暖的背景下,引起黑龙江西部水稻集中种植区向北推移了一个纬度左右的主要自然因素是热量条件的改善,故本题选择B。
2. 在水资源的社会循环个环节中,下列做法不够恰当的是
A. 取水--保护水源地 B. 输水--减少过程损耗
C. 用水--节约、综合利用 D. 排水--防止当地污染
[解析]本组题重点考查学生的读图能力及对水循环各环节的理解。图1以地表水体及③为界分为自然循环、社会循环,这也正是第一题的切入点。地表水体与水汽输送之间的水循环环节为蒸发,其余①为降水,②为地表径流,④跨流域调水,故第1题选B。在社会循环中,人类的排水活动若不对污染进行回收处理,则会导致当地环境污染,故第2题选D。
 水循环包括自然循环和社会循环。读图1,回答1-2.
水循环包括自然循环和社会循环。读图1,回答1-2.
1. 图中①②③④分别为
A. 蒸发、地表径流、跨流域调水、降水
B. 降水、地表径流、蒸发、跨流域调水
C. 跨流域调水、下渗、地下径流、蒸发
D. 降水、蒸发、地表径流、跨流域调水
30.(2009福建卷文)(本小题满分)2分)
等比数列 中,已知
中,已知


(I)求数列 的通项公式;
的通项公式;
(Ⅱ)若 分别为等差数列
分别为等差数列 的第3项和第5项,试求数列
的第3项和第5项,试求数列 的通项公式及前
的通项公式及前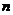 项和
项和 。
。
解:(I)设 的公比为
的公比为
由已知得 ,解得
,解得
(Ⅱ)由(I)得 ,
,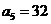 ,则
,则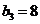 ,
,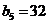
设 的公差为
的公差为 ,则有
,则有 解得
解得
从而
所以数列 的前
的前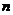 项和
项和
29.(2009天津卷理)(本小题满分14分)
已知等差数列{ }的公差为d(d
}的公差为d(d 0),等比数列{
0),等比数列{ }的公比为q(q>1)。设
}的公比为q(q>1)。设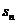 =
= +
+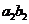 …..+
…..+
 ,
,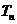 =
= -
-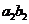 +…..+(-1
+…..+(-1
 ,n
,n
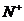
(I)
若 =
= =
1,d=2,q=3,求
=
1,d=2,q=3,求
 的值;
的值;
(II)
若 =1,证明(1-q)
=1,证明(1-q) -(1+q)
-(1+q) =
= ,n
,n
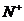 ;
;
(Ⅲ) 若正数n满足2 n
n q,设
q,设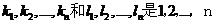 的两个不同的排列,
的两个不同的排列,  ,
,  证明
证明 。
。
本小题主要考查等差数列的通项公式、等比数列的通项公式与前n项和公式等基础知识,考查运算能力,推理论证能力及综合分析和解决问题的能力的能力,满分14分。
(Ⅰ)解:由题设,可得
所以,
(Ⅱ)证明:由题设可得 则
则
 ①
①
 ②
②
① 式减去②式,得
① 式加上②式,得
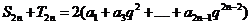 ③
③
② 式两边同乘q,得

所以,

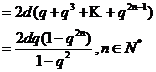
(Ⅲ)证明:


因为 所以
所以

(1) 若 ,取i=n
,取i=n
(2) 若 ,取i满足
,取i满足 且
且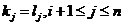
由(1),(2)及题设知,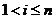 且
且

① 当 时,得
时,得
即 ,
, …,
…,
又 所以
所以

因此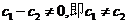
② 当 同理可得
同理可得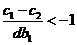 ,因此
,因此

综上,
28.(2009辽宁卷文)(本小题满分10分)
等比数列{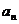 }的前n 项和为
}的前n 项和为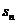 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列
(1)求{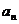 }的公比q;
}的公比q;
(2)求 -
- =3,求
=3,求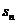


解:(Ⅰ)依题意有 


由于  ,故
,故

又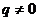 ,从而
,从而 5分
5分
(Ⅱ)由已知可得
故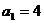
从而 10分
10分
27.(2009天津卷文)(本小题满分12分)
已知等差数列 的公差d不为0,设
的公差d不为0,设

(Ⅰ)若 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅱ)若 成等比数列,求q的值。
成等比数列,求q的值。
(Ⅲ)若
[答案](1) (2)
(2) (3)略
(3)略
[解析] (1)解:由题设,
代入解得 ,所以
,所以

(2)解:当 成等比数列,所以
成等比数列,所以 ,即
,即 ,注意到
,注意到 ,整理得
,整理得
(3)证明:由题设,可得 ,则
,则
 ①
①
 ②
②
①-②得,

①+②得,
 ③
③
③式两边同乘以 q,得
所以
(3)证明:
=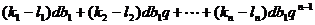
因为 ,所以
,所以

若 ,取i=n,
,取i=n,
若 ,取i满足
,取i满足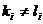 ,且
,且 ,
,
由(1)(2)及题设知, ,且
,且
 .
.


① 当 时,
时, ,由
,由 ,
,
即 ,
,

所以
因此
② 当 时,同理可得
时,同理可得 因此
因此 .
. 

综上,
[考点定位]本小题主要考查了等差数列的通项公式,等比数列通项公式与前n项和等基本知识,考查运算能力和推理论证能力和综合分析解决问题的能力。
26.(2009安徽卷文)(本小题满分12分)
已知数列{ } 的前n项和
} 的前n项和 ,数列{
,数列{ }的前n项和
}的前n项和
(Ⅰ)求数列{ }与{
}与{ }的通项公式;
}的通项公式;
(Ⅱ)设 ,证明:当且仅当n≥3时,
,证明:当且仅当n≥3时, <
< .
.


[思路]由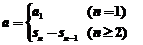 可求出
可求出 ,这是数列中求通项的常用方法之一,在求出
,这是数列中求通项的常用方法之一,在求出 后,进而得到
后,进而得到 ,接下来用作差法来比较大小,这也是一常用方法。
,接下来用作差法来比较大小,这也是一常用方法。
[解析](1)由于
当 时,
时, 

又当 时
时

 数列
数列 项与等比数列,其首项为1,公比为
项与等比数列,其首项为1,公比为
 .
. 

(2)由(1)知

由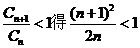 即
即 即
即
又 时
时 成立,即
成立,即 由于
由于 恒成立. .
恒成立. . 

因此,当且仅当 时,
时, 
25.(2009安徽卷理)(本小题满分13分)
首项为正数的数列 满足
满足


(I)证明:若 为奇数,则对一切
为奇数,则对一切 都是奇数;
都是奇数;
(II)若对一切 都有
都有 ,求
,求 的取值范围.
的取值范围.
解:本小题主要考查数列、数学归纳法和不等式的有关知识,考查推理论证、抽象概括、运算求解和探究能力,考查学生是否具有审慎思维的习惯和一定的数学视野。本小题满分13分。
解:(I)已知 是奇数,假设
是奇数,假设 是奇数,其中
是奇数,其中 为正整数,
为正整数,
则由递推关系得 是奇数。
是奇数。 

根据数学归纳法,对任何 ,
,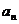 都是奇数。
都是奇数。
(II)(方法一)由 知,
知, 当且仅当
当且仅当 或
或 。
。
另一方面,若 则
则 ;若
;若 ,则
,则
根据数学归纳法,
综合所述,对一切 都有
都有 的充要条件是
的充要条件是 或
或 。
。
(方法二)由 得
得 于是
于是 或
或 。
。



因为 所以所有的
所以所有的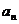 均大于0,因此
均大于0,因此 与
与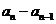 同号。
同号。
根据数学归纳法, ,
, 与
与 同号。
同号。 

因此,对一切 都有
都有 的充要条件是
的充要条件是 或
或 。
。
24.(2009广东卷理)(本小题满分14分). 

已知曲线 .从点
.从点 向曲线
向曲线 引斜率为
引斜率为 的切线
的切线 ,切点为
,切点为 .
.
(1)求数列 的通项公式;
的通项公式;
(2)证明: .
.
解:(1)设直线 :
: ,联立
,联立 得
得 ,则
,则 ,∴
,∴ (
( 舍去).
舍去). 

 ,即
,即 ,∴
,∴
(2)证明:∵ .
. 


∴
由于 ,可令函数
,可令函数 ,则
,则 ,令
,令 ,得
,得 ,给定区间
,给定区间 ,则有
,则有 ,则函数
,则函数 在
在 上单调递减,∴
上单调递减,∴ ,即
,即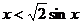 在
在 恒成立,又
恒成立,又 ,
,
则有 ,即
,即 .
. 
 .
. 

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com