
2、下列函数既是奇函数,又在区间 上单调递减的是( )
上单调递减的是( )
A、 B、
B、 C、
C、 D、
D、
1、若
 是奇函数,则下列各点中,在曲线
是奇函数,则下列各点中,在曲线 上的点是 ( )
上的点是 ( )
A、 B、
B、 C、
C、 D、
D、
5. (2006上海春)已知函数 是定义在
是定义在 上的偶函数. 当
上的偶函数. 当 时,
时,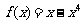 ,则当
,则当 时,
时, .
.
函数的奇偶性和周期性(作业)
4. (2006全国卷I)已知函数 ,若
,若 为奇函数,则
为奇函数,则 ________。
________。
3. (2006安徽卷)函数 对于任意实数
对于任意实数 满足条件
满足条件 ,若
,若 则
则 __________。
__________。
2. (07全国Ⅰ)设 ,
, 是定义在R上的函数,
是定义在R上的函数, ,则“
,则“ ,
, 均为偶函数”是“
均为偶函数”是“ 为偶函数”的( )
为偶函数”的( )
A.充要条件 B.充分不必要的条件C.必要不充分的条件D.既不充分也不必要的条件
(07江西)设函数f(x)是R上以5为周期的可导偶函数,则曲线y=f(x)在x=5处的切线的斜率为
A.- B.0 C.
B.0 C. D.5
D.5
(07安徽)定义在R上的函数 既是奇函数,又是周期函数,
既是奇函数,又是周期函数, 是它的一个正周期.若将方程
是它的一个正周期.若将方程 在闭区间
在闭区间 上的根的个数记为
上的根的个数记为 ,则
,则 可能为
可能为
A.0 B.1 C.3 D.5
(07天津)在 上定义的函数
上定义的函数 是偶函数,且
是偶函数,且 ,若
,若 在区间
在区间 是减函数,则函数
是减函数,则函数 ( )
( )
A.在区间 上是增函数,区间
上是增函数,区间 上是增函数
上是增函数
B.在区间 上是增函数,区间
上是增函数,区间 上是减函数
上是减函数
C.在区间 上是减函数,区间
上是减函数,区间 上是增函数
上是增函数
1. (2006福建卷)已知 是周期为2的奇函数,当
是周期为2的奇函数,当 时,
时, 设
设
 则( )
则( )
(A) (B)
(B) (C)
(C)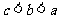 (D)
(D)
5.
设 是R上的任意函数,则下列叙述正确的是
A)
是R上的任意函数,则下列叙述正确的是
A) 是奇函数 B)
是奇函数 B) 是奇函数
C)
是奇函数
C)  是偶函数 (D)
是偶函数 (D)  是偶函数
是偶函数
[例题讲解]
例1:判断下列函数的奇偶性(先看定义域,后看f(x)与f(-x)关系)
1) 2)
2)
3)
例2:设 是
是 上的奇函数,
上的奇函数, ,当
,当 时,
时, ,则
,则 等于_______
等于_______
[变题]设 是定义在实数集R上的函数,且满足
是定义在实数集R上的函数,且满足 ,如果
,如果 ,
, ,求
,求
例3:设 是定义在
是定义在 上的奇函数,且
上的奇函数,且 ,又当
,又当 时,
时, ,(1)证明:直线
,(1)证明:直线 是函数
是函数 图象的一条对称轴:(2)当
图象的一条对称轴:(2)当 时,求
时,求 的解析式。
的解析式。
[变题]设 是定义在
是定义在 上的奇函数,且它的图象关于直线
上的奇函数,且它的图象关于直线 对称,求证:
对称,求证: 是周期函数.
是周期函数.
[命题展望]
4.
若函数f(x)是定义在R上的偶函数,在 上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是_______
上是减函数,且f(2)=0,则使得f(x)<0的x的取值范围是_______
3.
若函数 是定义在R上的奇函数,且当
是定义在R上的奇函数,且当 时,
时, ,那么当x∈(-∞,0)时,f(x) =_______
,那么当x∈(-∞,0)时,f(x) =_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com