
1. 方程 的实根的个数为( )
的实根的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
见优化设计。
[模拟试题]
数形结合思想是解答数学试题的的一种常用方法与技巧,特别是在解决选择、填空题是发挥着奇特功效,复习中要以熟练技能、方法为目标,加强这方面的训练,以提高解题能力和速度。
例1.
分析:

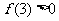 ,
,




例2. 
解:法一、常规解法:



法二、数形结合解法:





例3. 
A. 1个 B. 2个 C. 3个 D. 1个或2个或3个
分析:
出两个函数图象,易知两图象只有两个交点,故方程有2个实根,选(B)。

例4. 

分析:







例5. 
分析:
构造直线的截距的方法来求之。




截距。


例6. 

分析:
以3为半径的圆在x轴上方的部分,(如图),而N则表示一条直线,其斜率k=1,纵截




例7. 
MF1的中点,O表示原点,则|ON|=( )

分析:①设椭圆另一焦点为F2,(如图), 
 又注意到N、O各为MF1、F1F2的中点,
又注意到N、O各为MF1、F1F2的中点,
∴ON是△MF1F2的中位线, 
②若联想到第二定义,可以确定点M的坐标,进而求MF1中点的坐标,最后利用两点间的距离公式求出|ON|,但这样就增加了计算量,方法较之①显得有些复杂。
例8. 
分析:



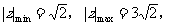



例9. 
解法一(代数法): ,
,




解法二(几何法):








例10. 
分析:
转化出一元二次函数求最值;倘若对式子平方处理,将会把问题复杂化,因此该题用常规解法显得比较困难,考虑到式中有两个根号,故可采用两步换元。
解:


第一象限的部分(包括端点)有公共点,(如图)


相切于第一象限时,u取最大值



4.数形结合的思想方法应用广泛,常见的如在解方程和解不等式问题中,在求函数的值域,最值问题中,在求复数和三角函数问题中,运用数形结合思想,不仅直观易发现解题途径,而且能避免复杂的计算与推理,大大简化了解题过程。这在解选择题、填空题中更显其优越,要注意培养这种思想意识,要争取胸中有图,见数想图,以开拓自己的思维视野。
3.纵观多年来的高考试题,巧妙运用数形结合的思想方法解决一些抽象的数学问题,可起到事半功倍的效果,数形结合的重点是研究“以形助数”。
2.实现数形结合,常与以下内容有关:①实数与数轴上的点的对应关系;②函数与图象的对应关系;③曲线与方程的对应关系;④以几何元素和几何条件为背景,建立起来的概念,如复数、三角函数等;⑤所给的等式或代数式的结构含有明显的几何意义。

1.数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题能迎刃而解,且解法简捷。所谓数形结合,就是根据数与形之间的对应关系,通过数与形的相互转化来解决数学问题的一种重要思想方法。数形结合思想通过“以形助数,以数解形”,使复杂问题简单化,抽象问题具体化能够变抽象思维为形象思维,有助于把握数学问题的本质,它是数学的规律性与灵活性的有机结合。
7.设双曲线C: 与直线
与直线 相交于两个不同的点A、B。
相交于两个不同的点A、B。
Ⅰ.求双曲线C的离心率 的取值范围;
的取值范围;
Ⅱ.设直线 与
与 轴的交点为P,且
轴的交点为P,且 ,求
,求 的值。
的值。
6.设 ,
, ,曲线
,曲线 在点
在点 处切线的倾斜角的取值范围为
处切线的倾斜角的取值范围为 ,则点P到曲线
,则点P到曲线 对称轴距离的取值范围是( )
对称轴距离的取值范围是( )




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com