
5.分段函数:(举一例)
3.理解分段函数的意义.通过对分段定义函数,复合函数,抽象函数等的认识,进一步体会函数关系的本质,进一步树立运动变化,相互联系、制约的函数思想,为函数思想的广泛运用打好基础.
4 克服“函数就是解析式”的片面认识,真正明确不仅函数的对应法则,而且其定义域都包含着对函数关系的制约作用,并真正以此作为处理问题的指导.
克服“函数就是解析式”的片面认识,真正明确不仅函数的对应法则,而且其定义域都包含着对函数关系的制约作用,并真正以此作为处理问题的指导.
5 函数的概念是复习函数全部内容和建立函数思想的基础,不能仅满足会背诵定义,会做一些有关题目,要从联系、应用的角度求得理解上的深度,还要对确定函数三要素的类型、方法作好系统梳理,这样才能进一步为综合运用打好基础.复习的重点是求得对这些问题的系统认识,而不是急于做过难的综合题.
函数的概念是复习函数全部内容和建立函数思想的基础,不能仅满足会背诵定义,会做一些有关题目,要从联系、应用的角度求得理解上的深度,还要对确定函数三要素的类型、方法作好系统梳理,这样才能进一步为综合运用打好基础.复习的重点是求得对这些问题的系统认识,而不是急于做过难的综合题.
知识点归纳
函数是一种特殊的映射,而映射是一种特殊的对应;函数的三要素中对应法则是核心,定义域是灵魂.
函数有二种定义,一是变量观点下的定义,一是映射观点下的定义.复习中不能仅满足对这两种定义的背诵,而应在判断是否构成函数关系,两个函数关系是否相同等问题中得到深化,更应在有关反函数问题中正确运用.
1 函数的定义:设A、B是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中x叫做自变量
函数的定义:设A、B是非空的数集,如果按某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数,记作y=f(x),x∈A,其中x叫做自变量 x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域
x的取值范围A叫做函数的定义域;与x的值相对应的y的值叫做函数值,函数值的集合{f(x)|x∈A}叫做函数的值域
2 两个函数的相等:函数的定义含有三个要素,即定义域A、值域C和对应法则f
两个函数的相等:函数的定义含有三个要素,即定义域A、值域C和对应法则f 当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定
当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定 因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数
因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数
3 映射的定义:一般地,设A、B是两个集合,如果按照某种对应关系f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,那么,这样的对应(包括集合A、B,以及集合A到集合B的对应关系f)叫做集合A到集合B的映射,记作f:A→B
映射的定义:一般地,设A、B是两个集合,如果按照某种对应关系f,对于集合A中的任何一个元素,在集合B中都有唯一的元素和它对应,那么,这样的对应(包括集合A、B,以及集合A到集合B的对应关系f)叫做集合A到集合B的映射,记作f:A→B
由映射和函数的定义可知,函数是一类特殊的映射,它要求A、B非空且皆为数集
4 映射的概念中象、原象的理解:(1) A中每一个元素都有象;(2)B中每一个元素不一定都有原象,不一定只一个原象;(3)A中每一个元素的象唯一
映射的概念中象、原象的理解:(1) A中每一个元素都有象;(2)B中每一个元素不一定都有原象,不一定只一个原象;(3)A中每一个元素的象唯一
2.能根据函数的三要素判断两个函数是否为同一函数;
1.了解映射的概念,在此基础上加深对函数概念的理解;
4. 已知函数 .
.
① 当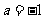 时,求函数的最大值和最小值;
时,求函数的最大值和最小值;
② 求实数 的取值范围,使
的取值范围,使 在区间
在区间 上是单调函数.
上是单调函数.
3. 利用函数的单调性求函数 的值域;
的值域;
2. 已知函数 的定义域为
的定义域为 ,且同时满足下列条件:(1)
,且同时满足下列条件:(1) 是奇函数;
是奇函数;
(2) 在定义域上单调递减;(3)
在定义域上单调递减;(3) 求
求 的取值范围.
的取值范围.
1. 判断一次函数 反比例函数
反比例函数 ,二次函数
,二次函数 的
的
单调性.
5. 下列四个命题
(1) 有意义; (2)函数是其定义域到值域的映射;
有意义; (2)函数是其定义域到值域的映射;
(3)函数 的图象是一直线;(4)函数
的图象是一直线;(4)函数 的图象是抛物线,
的图象是抛物线,
其中正确的命题个数是____________.
4. 若函数 是偶函数,则
是偶函数,则 的递减区间是
.
的递减区间是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com