
7.若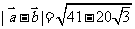 ,
,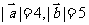 ,则
,则 的数量积为
( )
的数量积为
( )
A.10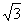 B.-10
B.-10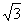 C.10
C.10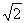 D.10
D.10
6.与向量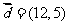 平行的单位向量为 ( )
平行的单位向量为 ( )
A.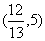 B.
B.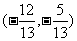 C.
C.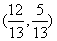 或
或 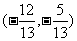 D.
D.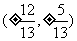
5.已知平行四边形三个顶点的坐标分别为(-1,0),(3,0),(1,-5),则第四个点的坐标为 ( )
A.(1,5)或(5,-5) B.(1,5)或(-3,-5)
C.(5,-5)或(-3,-5) D.(1,5)或(-3,-5)或(5,-5)
4.已知向量 反向,下列等式中成立的是 ( )
反向,下列等式中成立的是 ( )
A.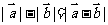 B.
B.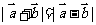
C.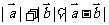 D.
D.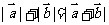
3. 在 ABCD中,设
在 ABCD中,设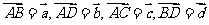 ,则下列等式中不正确的是( )
,则下列等式中不正确的是( )
A.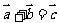 B.
B.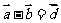 C.
C. D.
D.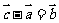
2.对于菱形ABCD,给出下列各式: ①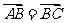 ②
②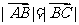
③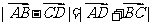 ④
④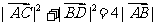 2其中正确的个数为 ( )
2其中正确的个数为 ( )
A.1个 B.2个 C.3个 D.4个
1.在矩形ABCD中,O是对角线的交点,若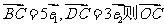 =(
)
=(
)
A.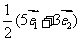 B.
B.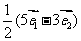 C.
C.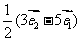 D.
D.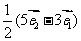
例1、若直线mx+y+2=0与线段AB有交点,其中A(-2, 3),B(3,2),求实数m的取值范围。
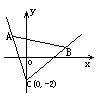 解:直线mx+y+2=0过一定点C(0,
-2),直线mx+y+2=0实际上表示的是过定点(0, -2)的直线系,因为直线与线段AB有交点,则直线只能落在∠ABC的内部,设BC、CA这两条直线的斜率分别为k1、k2,则由斜率的定义可知,直线mx+y+2=0的斜率k应满足k≥k1或k≤k2, ∵A(-2,
3) B(3, 2)
解:直线mx+y+2=0过一定点C(0,
-2),直线mx+y+2=0实际上表示的是过定点(0, -2)的直线系,因为直线与线段AB有交点,则直线只能落在∠ABC的内部,设BC、CA这两条直线的斜率分别为k1、k2,则由斜率的定义可知,直线mx+y+2=0的斜率k应满足k≥k1或k≤k2, ∵A(-2,
3) B(3, 2)
∴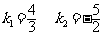
∴-m≥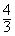 或-m≤
或-m≤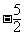 即m≤
即m≤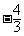 或m≥
或m≥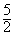
说明:此例是典型的运用数形结合的思想来解题的问题,这里要清楚直线mx+y+2=0的斜率-m应为倾角的正切,而当倾角在(0°,90°)或(90°,180°)内,角的正切函数都是单调递增的,因此当直线在∠ACB内部变化时,k应大于或等于kBC,或者k小于或等于kAC,当A、B两点的坐标变化时,也要能求出m的范围。
例2、已知x、y满足约束条件
 x≥1,
x≥1,
x-3y≤-4,
3x+5y≤30,
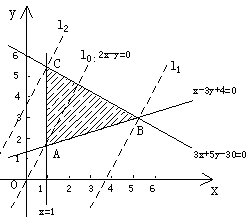 求目标函数z=2x-y的最大值和最小值.
求目标函数z=2x-y的最大值和最小值.
解:根据x、y满足的约束条件作出可行域,即如图所示的阴影部分(包括边界).
作直线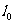 :2x-y=0,再作一组平行于
:2x-y=0,再作一组平行于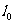 的直线
的直线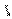 :2x-y=t,t∈R.
:2x-y=t,t∈R.
可知,当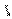 在
在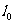 的右下方时,直线
的右下方时,直线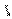 上的点(x,y)满足2x-y>0,即t>0,而且直线
上的点(x,y)满足2x-y>0,即t>0,而且直线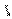 往右平移时,t随之增大.当直线
往右平移时,t随之增大.当直线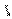 平移至
平移至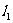 的位置时,直线经过可行域上的点B,此时所对应的t最大;当
的位置时,直线经过可行域上的点B,此时所对应的t最大;当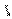 在
在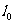 的左上方时,直线
的左上方时,直线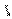 上的点(x,y)满足2x-y<0,即t<0,而且直线
上的点(x,y)满足2x-y<0,即t<0,而且直线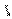 往左平移时,t随之减小.当直线
往左平移时,t随之减小.当直线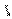 平移至
平移至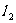 的位置时,直线经过可行域上的点C,此时所对应的t最小.
的位置时,直线经过可行域上的点C,此时所对应的t最小.
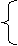 x-3y+4=0,
x-3y+4=0,
由 解得点B的坐标为(5,3);
3x+5y-30=0,
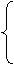 x=1,
x=1,
由
解得点C的坐标为(1,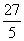 ).
).
3x+5y-30=0,
所以,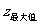 =2×5-3=7;
=2×5-3=7;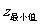 =2×1-
=2×1-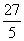 =
=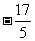 .
.
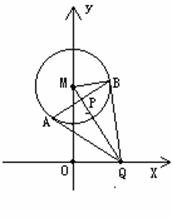
例3、 已知⊙M: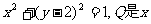 轴上的动点,QA,QB分别切⊙M于A,B两点,(1)如果
轴上的动点,QA,QB分别切⊙M于A,B两点,(1)如果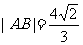 ,求直线MQ的方程;
,求直线MQ的方程;
(2)求动弦AB的中点P的轨迹方程.
解:(1)由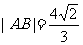 ,可得
,可得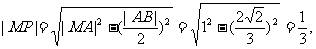 由射影定理,得
由射影定理,得 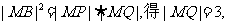 在Rt△MOQ中,
在Rt△MOQ中,
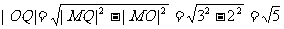 ,
,
故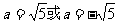 ,
,
所以直线AB方程是
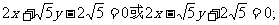
(2)连接MB,MQ,设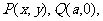 由
由
点M,P,Q在一直线上,得
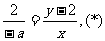 由射影定理得
由射影定理得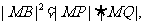
即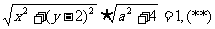 把(*)及(**)消去a,
把(*)及(**)消去a,
并注意到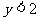 ,可得
,可得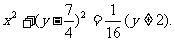
说明:适时应用平面几何知识,这是快速解答本题的要害所在。
例4、已知双曲线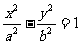 的离心率
的离心率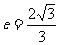 ,过
,过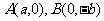 的直线到原点的距离是
的直线到原点的距离是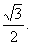 (1)求双曲线的方程;
(1)求双曲线的方程;
(2)已知直线 交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
交双曲线于不同的点C,D且C,D都在以B为圆心的圆上,求k的值.
解:∵(1)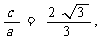 原点到直线AB:
原点到直线AB: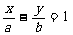 的距离
的距离 .
.
故所求双曲线方程为 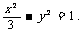
(2)把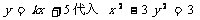 中消去y,整理得
中消去y,整理得 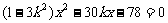 .
.
设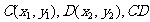 的中点是
的中点是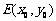 ,则
,则

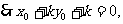
即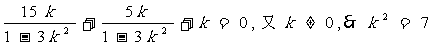
故所求k=±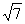 .
.
说明:为了求出 的值, 需要通过消元, 想法设法建构
的值, 需要通过消元, 想法设法建构 的方程.
的方程.
例5、已知椭圆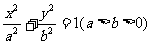 的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点
的长、短轴端点分别为A、B,从此椭圆上一点M向x轴作垂线,恰好通过椭圆的左焦点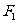 ,向量
,向量 与
与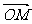 是共线向量。
是共线向量。
(1)求椭圆的离心率e;
(2)设Q是椭圆上任意一点,
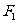 、
、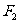 分别是左、右焦点,求∠
分别是左、右焦点,求∠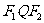 的取值范围;
的取值范围;
解:(1)∵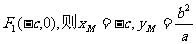 ,∴
,∴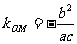 。
。
∵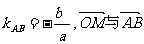 是共线向量,∴
是共线向量,∴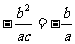 ,∴b=c,故
,∴b=c,故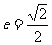 。
。
(2)设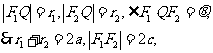
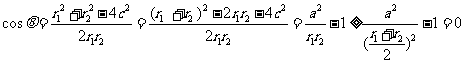
当且仅当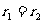 时,cosθ=0,∴θ
时,cosθ=0,∴θ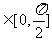 。
。
说明:由于共线向量与解析几何中平行线、三点共线等具有异曲同工的作用,因此,解析几何中与平行线、三点共线等相关的问题均可在向量共线的新情景下设计问题。求解此类问题的关键是:正确理解向量共线与解析几何中平行、三点共线等的关系,把有关向量的问题转化为解析几何问题。
3.注意强化思维的严谨性,力求规范解题,尽可能少丢分
在解解析几何的大题时,有不少学生常出现因解题不够规范而丢分的现象,因此,要通过平时的讲评对易出现错误的相关步骤作必要的强调,减少或避免无畏的丢分.
例14(04全国文科Ⅰ)设双曲线C: 相交于两个不同的点A、B.
相交于两个不同的点A、B.
(I)求双曲线C的离心率e的取值范围:
(II)设直线l与y轴的交点为P,且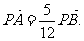 求a的值.
求a的值.
解:(I)由C与t相交于两个不同的点,故知方程组
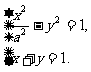 有两个不同的实数解.消去y并整理得
有两个不同的实数解.消去y并整理得
(1-a2)x2+2a2x-2a2=0. ①

双曲线的离心率

还有,在设直线方程为点斜式时,就应该注意到直线斜率不存在的情形;又如,在求轨迹方程时,还要注意到纯粹性和完备性等.
2.重视通性通法,加强解题指导,提高解题能力
在二轮复习中,不能仅仅复习概念和性质,还应该以典型的例题和习题(可以选用04年的各地高考试题和近两年的各地高考模拟试题)为载体,在二轮复习中强化各类问题的常规解法,使学生形成解决各种类型问题的操作范式.数学学习是学生自主学习的过程,解题能力只有通过学生的自主探究才能掌握.所以,在二轮复习中,教师的作用是对学生的解题方法进行引导、点拨和点评,只有这样,才能够实施有效复习.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com