2、机械能守恒定律

(1)内容：在只有重力或弹力做功的物体系统内，动能和弹性势能可以相互转化，而总的机械能保持不变。这就是机械能守恒定律。

(2)表达式：或

(3)机械能守恒条件的理解

1、动能与势能的相互转化

4.根据机械能守恒定律的不同表达式列方程，并求解结果。

(2)应用机械能守恒定律解题的优点

机械能守恒定律不涉及运动过程中的加速度和时间，用它来处理问题要比牛顿定律方便；应用机械能守恒定律解决问题，只需考虑运动的始末状态，不必考虑两个状态之间过程的细节。如果直接用牛顿运动定律解决问题，往往要分析过程中各个力的作用，而这些力往往又是变化的，因此一些难以用牛顿运动定律解决的问题，应用机械能守恒定律则易于解决。

板书设计：

第八节　 机械能守恒定律

3.恰当地选取零势能面，确定研究对象在过程中的始态或末态的机械能。

2.明确研究对象的运动过程，分析对象在过程中的受力情况，弄清各力做功的情况，判断机械能是否守恒。

1.根据题意选取研究对象(物体或系统)

3、守恒定律的多种表达方式

　　 当系统满足机械能守恒的条件以后，常见的守恒表达式有以下几种：

(1)，即初状态的动能和势能之和等于末状态的动能和势能之和。

(2)，即动能(或势能)的增加量等于势能(或动能)的减少量。

(3)，即A物体机械能的增加量等于B物体机械能的减少量。

把一个小球用细绳悬挂起来，就成为一个摆(如图)，摆长为l 　,最大偏角为θ .小球运动到最低位置时的速度是多大？

分析：这个问题直接用牛顿第二定律和运动学的公式来处理，需要用高等数学。现在用机械能守恒定律求解。

提问：你是怎样判断这种情况下机械能守恒的？

解：选择小球在最低位置时所在的水平面为参考平面。

小球在最高点时为初状态，初状态的动能E _k1 = 0 ，

重力势能E _p1 = mg ( l -l cosθ )

机械能E_k1+E_p1=mg ( l - l cosθ )

小球在最低点时为末状态，末状态的动能 =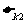

重力势能

末状态的机械能为.

根据机械能守恒定律有　

即　 　　　所以　 = 　.

思考：你能不能直接用牛顿第二定律和运动学的公式来处理这个问题 ？应用机械能守恒定律解题的优越性。

(1)机械能守恒定律解题的一般步骤

2.除重力或弹力外，还受其它力，但其它力不做功或其它力所做功代数和为零(如摆球的摆动)。

例1： A、B间，B与地面间摩擦不计，A自B上自由下滑过程中，A、B组成的系统只有重力和A、B间的弹力(系统内的弹力)做功，A、B组成的系统的机械能守恒，但对B来说，A对B的弹力做功，但这个力对B来说是外力，B的机械能不守恒。同样对A来说，A的机械能不守恒。

说明：如果问题中只有动能和重力势能的相互转化，没有涉及到弹性势能，此时机械能守恒的条件可以表述为：只有重力做功以后遇到的问题绝大多数都是这种情形。

1.只受重力或弹力；

2.从系统做功的角度看，只有重力或弹力做功。

(4)只有重力或弹力做功与只受重力或弹力作用的含义不同。