
96. [2010 •辽宁文数]
设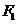 ,
,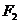 分别为椭圆
分别为椭圆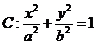
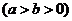 的左、右焦点,过
的左、右焦点,过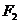 的直线
的直线 与椭圆
与椭圆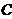 相交于
相交于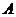 ,
,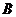 两点,直线
两点,直线 的倾斜角为
的倾斜角为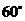 ,
,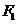 到直线
到直线 的距离为
的距离为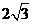 .
.
(Ⅰ)求椭圆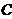 的焦距;
的焦距;
(Ⅱ)如果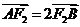 ,求椭圆
,求椭圆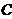 的方程.
的方程.
解:(Ⅰ)设焦距为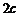 ,由已知可得
,由已知可得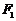 到直线l的距离
到直线l的距离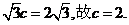
所以椭圆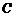 的焦距为4.
的焦距为4.
(Ⅱ)设 直线
直线 的方程为
的方程为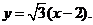
联立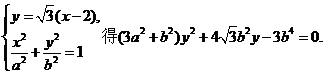
解得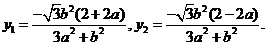
因为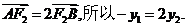
即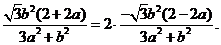
得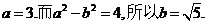
故椭圆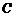 的方程为
的方程为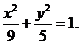
95.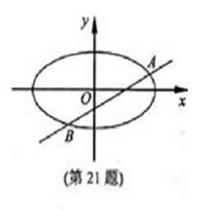 [2010•浙江理数]已知m>1,直线
[2010•浙江理数]已知m>1,直线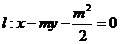 ,椭圆
,椭圆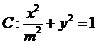 ,
,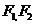 分别为椭圆
分别为椭圆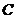 的左、右焦点.
的左、右焦点.
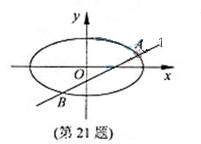
(Ⅰ)当直线 过右焦点
过右焦点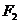 时,求直线
时,求直线 的方程;
的方程;
(Ⅱ)设直线 与椭圆
与椭圆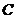 交于
交于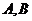 两点,
两点,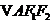 ,
,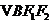 的重心分别为
的重心分别为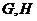 .若原点
.若原点 在以线段
在以线段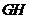 为直径的圆内,求实数
为直径的圆内,求实数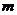 的取值范围.
的取值范围.
[解析]本题主要考察椭圆的几何性质,直线与椭圆,点与圆的位置关系等基础知识,同时考察解析几何的基本思想方法和综合解题能力。
解: (Ⅰ)因为直线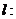
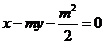 经过
经过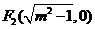 ,所以
,所以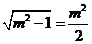 ,得
,得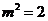 ,
,
又因为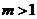 ,所以
,所以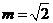 ,
,
故直线 的方程为
的方程为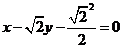 。
。
 (Ⅱ)设
(Ⅱ)设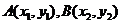 。
。
由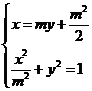 ,消去
,消去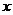 得
得
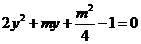
则由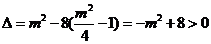 ,知
,知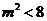 ,
,
且有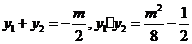 。
。
由于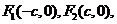 ,
,
故 为
为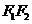 的中点,
的中点,
由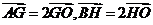 ,
,
可知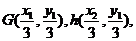
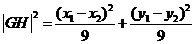
设 是
是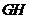 的中点,则
的中点,则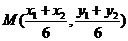 ,
,
由题意可知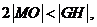
即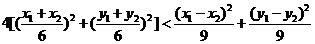
即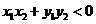
而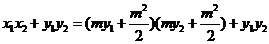
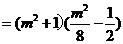
所以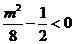
即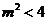
又因为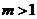 且
且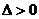
所以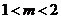 。
。
所以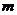 的取值范围是
的取值范围是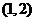 。
。
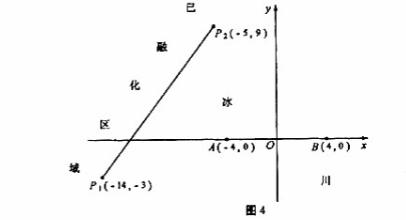
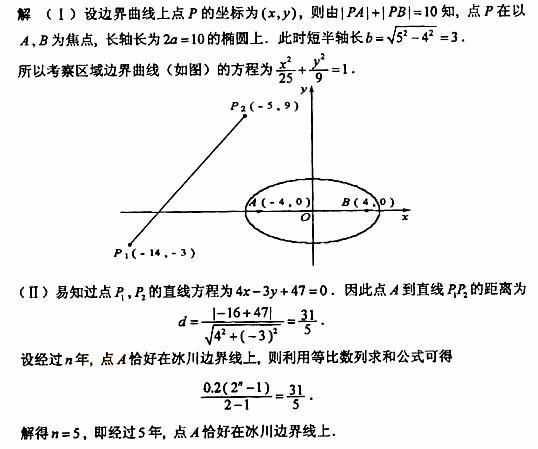
94. [2010•湖南文数]为了考察冰川的融化状况,一支科考队在某冰川山上相距8Km的A、B两点各建一个考察基地,视冰川面为平面形,以过A、B两点的直线为x轴,线段AB的垂直平分线为y轴建立平面直角坐标系(图4)。考察范围到A、B两点的距离之和不超过10Km的区域。
(I) 求考察区域边界曲线的方程:
(II)
如图4所示,设线段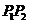 是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
是冰川的部分边界线(不考虑其他边界),当冰川融化时,边界线沿与其垂直的方向朝考察区域平行移动,第一年移动0.2km,以后每年移动的距离为前一年的2倍。问:经过多长时间,点A恰好在冰川边界线上?
93. [2010•上海文数]已知椭圆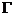 的方程为
的方程为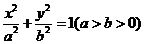 ,
,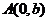 、
、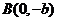 和
和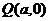 为
为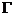 的三个顶点.
的三个顶点.
(1)若点 满足
满足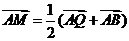 ,求点
,求点 的坐标;
的坐标;
(2)设直线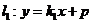 交椭圆
交椭圆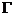 于
于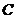 、
、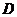 两点,交直线
两点,交直线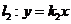 于点
于点 .若
.若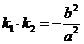 ,证明:
,证明: 为
为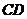 的中点;
的中点;
(3)设点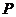 在椭圆
在椭圆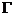 内且不在
内且不在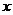 轴上,如何构作过
轴上,如何构作过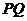 中点
中点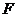 的直线
的直线 ,使得
,使得 与椭圆
与椭圆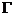 的两个交点
的两个交点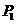 、
、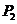 满足
满足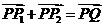
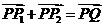 ?令
?令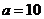 ,
,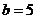 ,点
,点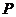 的坐标是(-8,-1),若椭圆
的坐标是(-8,-1),若椭圆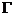 上的点
上的点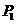 、
、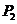 满足
满足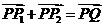 ,求点
,求点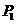 、
、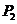 的坐标.
的坐标.
解:(1) 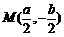 ;
(2) 由方程组
;
(2) 由方程组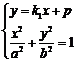 ,消y得方程
,消y得方程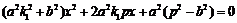 ,
因为直线
,
因为直线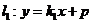 交椭圆
交椭圆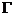 于
于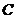 、
、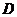 两点,
所以D>0,即
两点,
所以D>0,即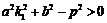 ,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则
,
设C(x1,y1)、D(x2,y2),CD中点坐标为(x0,y0),
则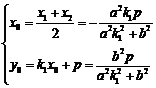 ,
由方程组
,
由方程组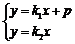 ,消y得方程(k2-k1)x=p,
又因为
,消y得方程(k2-k1)x=p,
又因为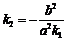 ,所以
,所以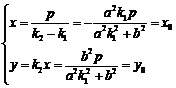 ,
故E为CD的中点;
(3) 因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由
,
故E为CD的中点;
(3) 因为点P在椭圆Γ内且不在x轴上,所以点F在椭圆Γ内,可以求得直线OF的斜率k2,由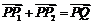 知F为P1P2的中点,根据(2)可得直线l的斜率
知F为P1P2的中点,根据(2)可得直线l的斜率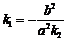 ,从而得直线l的方程.
,从而得直线l的方程.
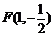 ,直线OF的斜率
,直线OF的斜率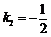 ,直线l的斜率
,直线l的斜率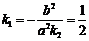 ,
解方程组
,
解方程组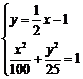 ,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3).
,消y:x2-2x-48=0,解得P1(-6,-4)、P2(8,3).
92.[2010·湖北省襄樊五中5月调研]从双曲线-=1的左焦点F引圆x2 + y2 = 3的切线FP交双曲线右支于点P,T为切点,M为线段FP的中点,O为坐标原点,则| MO | – | MT | 等于 。
[答案]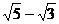
[解析]设双曲线的右焦点为F1,因为O为FF1中点,M为PF中点,所以MO为三角形PFF1的中位线,|MO|=|PF1|,又|MT|=|PT|-|PM|=|PF|-|FT|-|PF|=|PF|-|FT|,所以|MO|-|MT|=(|PF1|-|PF|)+|FT|=|FT|-a,又a=,|FT|==。所以|MO|-|MT|=-。
91.[2010·河南省郑州市第二次质检]已知直线l过抛物线x2=ay(a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a=_____________.
[答案]4
[解析]易知直线l被抛物线截得的弦长为抛物线的通径2p=a=4.
90.[2010湖北省普通高等学校招生全国统一考试模拟训练(二)]抛物线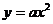 的准线方程是
的准线方程是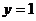 ,则
,则 的值为
.
的值为
.
[答案]―
[解析]将抛物线化为标准方程:x2=y,因为其准线为y=1,所以a<0,从而其准线方程为y=-=1,解得a=―。
89.[2010·甘肃省兰州市五月实战模拟]已知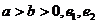 分别是圆锥曲线
分别是圆锥曲线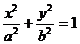 和
和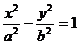 的离心率,设
的离心率,设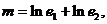 则m的取值范围是
。
则m的取值范围是
。
[答案]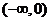
[解析]由条件得: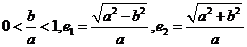 ,则
,则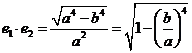
得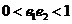 ,所以
,所以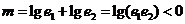 .
.
88.[2010·广东省四月调研]已知点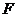 、
、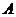 分别为双曲线
分别为双曲线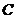 :
: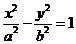
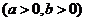 的
的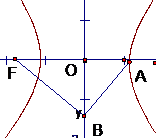 左焦点、右顶点,点
左焦点、右顶点,点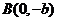 满足
满足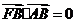 ,则双曲线的离心率为
。
,则双曲线的离心率为
。
[答案]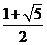
[解析]如图,∵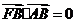 ,∴
,∴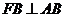 ,则
,则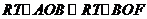 ,
,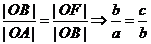 ,
,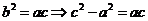
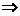
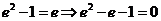 ,∴
,∴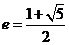
87.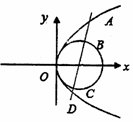 [2010·河北省衡水中学一模] 如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|·|CD|=____________。
[2010·河北省衡水中学一模] 如图,过抛物线y2=4x的焦点F的直线交抛物线与圆(x-1)2+y2=1于A,B,C,D四点,则|AB|·|CD|=____________。
[答案]1
[解析]由特殊化原则,当直线过焦点F且垂直于x轴时,|AD|=2p=4,|BC|=2r=2,由抛物线与圆的对称性知:|AB|=|CD|=1,所以|AB|·|CD|=1。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com