
116.[2010·广东省四月调研]已知定点A(0,-1),点B在圆 上运动,
上运动,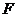 为圆心,线段AB的垂直平分线交BF于P.
为圆心,线段AB的垂直平分线交BF于P.
 (I)求动点P的轨迹
(I)求动点P的轨迹 的方程;若曲线
的方程;若曲线 被轨迹
被轨迹 包围着,求实数
包围着,求实数 的最小值。
的最小值。
(II)已知 、
、 ,动点
,动点 在圆
在圆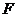 内,且满足
内,且满足 ,求
,求 的取值范围.
的取值范围.
解:(I)由题意得 ,∴
,∴
∴P点轨迹是以A、F为焦点的椭圆.设椭圆方程为
 ,
,
则 ,∴点
,∴点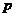 的轨迹方程为
的轨迹方程为
曲线 化为
化为 ,
,
则曲线 是圆心在
是圆心在 ,半径为1的圆。而轨迹E:
,半径为1的圆。而轨迹E: 为焦点在Y轴上的椭圆,短轴上的顶点为
为焦点在Y轴上的椭圆,短轴上的顶点为 结合它们的图像知:若曲线
结合它们的图像知:若曲线 被轨迹E包围着,则
被轨迹E包围着,则 ,∴
,∴ 的最小值为
的最小值为 。
。
(II))设 ,由
,由 得:
得: ,
,
化简得 ,即
,即 ,
,
而


∵点 在圆
在圆 内,∴
内,∴
∴ ,
,
∴ ,∴
,∴ 的取值范围为
的取值范围为 .
.
115.[2010·巢湖市第一学期期末质检]已知椭圆的中心在原点,焦点 在
在 轴的非负半轴上,点
轴的非负半轴上,点 到短轴端点的距离是4,椭圆上的点到焦点
到短轴端点的距离是4,椭圆上的点到焦点 距离的最大值是6.
距离的最大值是6.
(Ⅰ)求椭圆的标准方程和离心率 ;
;
(Ⅱ)若 为焦点
为焦点 关于直线
关于直线 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使 到点
到点 的距离为定值?若存在,求出点
的距离为定值?若存在,求出点 的坐标及此定值;若不存在,请说明理由.
的坐标及此定值;若不存在,请说明理由.
解:(Ⅰ)设椭圆长半轴长及半焦距分别为 ,由已知得
,由已知得
 .
.
所以椭圆的标准方程为 . 离心率
. 离心率
(Ⅱ) ,设
,设 由
由 得
得

化简得 ,即
,即
故存在一个定点 ,使
,使 到
到 点的距离为定值,其定值为
点的距离为定值,其定值为
114.[2010·海淀一模]已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在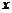 轴上,左右焦点分别为
轴上,左右焦点分别为 ,
, ,且
,且 ,点
,点 在椭圆
在椭圆 上.
上.
⑴求椭圆 的方程;
的方程;
⑵过 的直线
的直线 与椭圆
与椭圆 相交于
相交于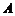 、
、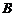 两点,且
两点,且 的面积为
的面积为 ,求以
,求以 为圆心且与直线
为圆心且与直线 相切的圆的方程.
相切的圆的方程.
解:⑴设椭圆的方程为 ,由题意可得:椭圆
,由题意可得:椭圆 两焦点坐标分别为
两焦点坐标分别为 ,
, .∴
.∴ .∴
.∴ ,又
,又 ,
,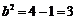 ,故椭圆的方程为
,故椭圆的方程为 .
.
⑵当直线
 轴,计算得到:
轴,计算得到: ,
, ,
, ,不符合题意.当直线
,不符合题意.当直线 与
与 轴不垂直时,设直线
轴不垂直时,设直线 的方程为:
的方程为: ,由
,由 ,消去y得
,消去y得 .显然
.显然 成立,设
成立,设 ,
, ,则
,则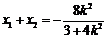 ,
, .
.
又
即 ,又圆
,又圆 的半径
的半径 .
.
所以 ,
,
化简,得 ,即
,即 ,解得
,解得 .所以,
.所以, .
.
故圆 的方程为:
的方程为: .
.
⑵另解:设直线 的方程为
的方程为 ,由
,由 ,消去
,消去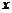 得
得 ,
, 恒成立,设
恒成立,设 ,
, ,则
,则 ,
, .
.
所以

 .
.
又圆 的半径为
的半径为
 .
.
所以


 ,解得
,解得 ,
,
所以
 .故圆
.故圆 的方程为:
的方程为: .
.
113.[2010·湖南师大附中第二次月]已知抛物线C的顶点在坐标原点,焦点在x轴上,P(2,0)为定点.
(Ⅰ)若点P为抛物线的焦点,求抛物线C的方程;
(Ⅱ)若动圆M过点P,且圆心M在抛物线C上运动,点A、B是圆M与 轴的两交点,试推断是否存在一条抛物线C,使|AB|为定值?若存在,求这个定值;若不存在,说明理由.
轴的两交点,试推断是否存在一条抛物线C,使|AB|为定值?若存在,求这个定值;若不存在,说明理由.
解:(Ⅰ) 设抛物线方程为 ,则抛物线的焦点坐标为
,则抛物线的焦点坐标为 .由已知,
.由已知, ,即
,即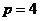 ,故抛物线C的方程是
,故抛物线C的方程是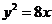 .
.
(Ⅱ)设圆心 (
( ),点A
),点A ,B
,B .
因为圆
.
因为圆 过点P(2,0),则可设圆M的方程为
过点P(2,0),则可设圆M的方程为 . 令
. 令 ,得
,得 .则
.则 ,
, . 所以
. 所以 . ,设抛物线C的方程为
. ,设抛物线C的方程为 ,因为圆心M在抛物线C上,则
,因为圆心M在抛物线C上,则 . 所以
. 所以 . 由此可得,当
. 由此可得,当 时,
时,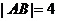 为定值.故存在一条抛物线
为定值.故存在一条抛物线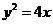 ,使|AB|为定值4.
,使|AB|为定值4.
112.[2010·石家庄市质检(二)]已知抛物线方程x2=4y,过点(t,-4)作抛物线的两条切线PA、PB,切点分别为A、B.
(I)求证直线AB过定点(0,4);
(II)求 OAB(O为坐标原点)面积的最小值.
OAB(O为坐标原点)面积的最小值.
解:(Ⅰ)设切点为
 又
又  , 则切线
, 则切线 的方程为:
的方程为:  , 即
, 即 , 切线
, 切线 的方程为:
的方程为: 即
即 ,由(t,―4)是
,由(t,―4)是 、
、 交点可知:
交点可知:  ,
,  , ∴过A、B的直线方程为
, ∴过A、B的直线方程为 , 即
, 即 , 所以直线
, 所以直线 过定点(0,4).
过定点(0,4).
(Ⅱ)由 ,得
,得 .则
.则 , 因为
, 因为
 =
= ,当且仅当t=0时,
,当且仅当t=0时,
111.[2010·福建漳州一中年五月质检]已知椭圆 ,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且
,直线l与椭圆交于A、B两点,M是线段AB的中点,连接OM并延长交椭圆于点C.直线AB与直线OM的斜率分别为k、m,且 .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)若直线AB经过椭圆的右焦点F,问:对于任意给定的不等于零的实数k,是否存在a∈[2,+∞],使得四边形OACB是平行四边形,请证明你的结论。

解:(Ⅰ)解法一:设 ,
, ,
, ,则
,则 ,
,
两式相减,得: ,又
,又 ,
, ,
,
∴ ,
,
又∵ ,
, ∴
∴ ,∴
,∴
解法二:设直线AB的方程为y=kx+n,代入椭圆方程得 ,设
,设 ,
, ,
, ,则
,则 ,∴
,∴ ,
, ,
,
∴ ,又
,又 ∴
∴ ,∴
,∴
(Ⅱ)设C(xC,yC),直线AB的方程为y=k(x-c)(k≠0),代入椭圆方程 ,得
,得 ,若OACB是平行四边形,则
,若OACB是平行四边形,则 ,∴
,∴ ,
, ,∵C在椭圆上 ∴
,∵C在椭圆上 ∴ ∴
∴ ,∴
,∴ ,∴
,∴ ∴
∴ ,∵
,∵ ,a∈[2,+∞] ,∴
,a∈[2,+∞] ,∴ ,∴
,∴ 且
且 ,∴当
,∴当 且
且 时,存在a∈[2,+∞],使得四边形OACB是平行四边形;当
时,存在a∈[2,+∞],使得四边形OACB是平行四边形;当 或
或 时,不存在a∈[2,+∞],使得四边形OACB是平行四边形。
时,不存在a∈[2,+∞],使得四边形OACB是平行四边形。
110.[2010·北京海淀第二学期期中练习]已知椭圆C的对称中心为原点O,焦点在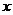 轴上,离心率为
轴上,离心率为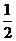 ,且点
,且点 在该椭圆上.
在该椭圆上.
(I)求椭圆C的方程;
(II)过椭圆C的左焦点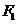 的直线
的直线 与椭圆C相交于A,B两点,若
与椭圆C相交于A,B两点,若 的面积为
的面积为 ,求圆心在原点O且与直线l相切的圆的方程.
,求圆心在原点O且与直线l相切的圆的方程.
解:(I)设椭圆C的方程为 ,由题意可得
,由题意可得 ,
,
又 ,因为椭圆C经过
,因为椭圆C经过 ,代入椭圆方程有
,代入椭圆方程有 ,解得
,解得 ,所以
,所以 故椭圆C的方程为
故椭圆C的方程为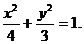
(II)解法一: 当直线l 轴时,计算得到:
轴时,计算得到:
 ,不符合题意。当直线l与x轴不垂直时,设直线l的方程为:
,不符合题意。当直线l与x轴不垂直时,设直线l的方程为: ,由
,由
显然 ,则
,则
又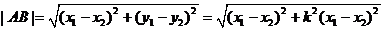

=
即 ,又圆O的半径
,又圆O的半径
所以
化简,得
解得 (舍),所以,
(舍),所以, 故圆O的方程为:
故圆O的方程为:
(II)解法二:设直线 的方程为
的方程为 ,
,
由
 ,因为
,因为 ,
,
则
所以

所以 ,
,
化简得到 ,解得
,解得 (舍),
(舍),
又圆O的半径为 ,所以
,所以 ,故圆O的方程为:
,故圆O的方程为: ;
;
109.[2010·江西省重点中学]第二次联考]已知动圆P过点 并且与圆
并且与圆 相外切,动圆圆心P的轨迹为W,过点N的直线
相外切,动圆圆心P的轨迹为W,过点N的直线 与轨迹W交于A、B两点。
与轨迹W交于A、B两点。
(1)求轨迹W的方程;
(2)若 ,求直线
,求直线 的方程;
的方程;
(3)对于 的任意一确定的位置,在直线
的任意一确定的位置,在直线 上是否存在一点Q,使得
上是否存在一点Q,使得 ,并说明理由。
,并说明理由。
解:(1)依题意可知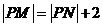 ∴
∴ ,∴点P的轨迹W是以M、N为焦点的双曲线的右支,设其方程为
,∴点P的轨迹W是以M、N为焦点的双曲线的右支,设其方程为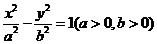 则
则 ∴
∴ ,∴轨迹W的方程为
,∴轨迹W的方程为
(2)当 的斜率不存在时,显然不满足
的斜率不存在时,显然不满足 ,故
,故 的斜率存在,设
的斜率存在,设 的方程为
的方程为 ,由
,由 得
得 ,又设
,又设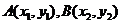 ,则
,则
由①②③解得 ,∵
,∵ ∴
∴
∴ 代入①②得
代入①②得 ,
,
消去 得
得 ,即
,即 ,故所求直线
,故所求直线 的方程为:
的方程为: ;
;
(3)问题等价于判断以AB为直径的圆是否与直线 有公共点
有公共点
若直线 的斜率不存在,则以AB为直径的圆为
的斜率不存在,则以AB为直径的圆为 ,可知其与直线
,可知其与直线 相交;若直线
相交;若直线 的斜率存在,则设直线
的斜率存在,则设直线 的方程为
的方程为 ,
,
由(2)知 且
且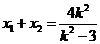 ,又
,又 为双曲线的右焦点,双曲线的离心率e=2,则
为双曲线的右焦点,双曲线的离心率e=2,则
设以AB为直径的圆的圆心为S,点S到直径 的距离为d,则
的距离为d,则
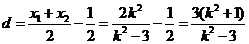
∴
∵ ∴
∴ 即
即 ,即直线
,即直线 与圆S相交。综上所述,以线段AB为直径的圆与直线
与圆S相交。综上所述,以线段AB为直径的圆与直线 相交;
相交;
故对于 的任意一确定的位置,与直线
的任意一确定的位置,与直线 上存在一点Q(实际上存在两点)使得
上存在一点Q(实际上存在两点)使得
108.[2010·巢湖市第一学期期末质检]已知椭圆的中心在原点,焦点 在
在 轴的非负半轴上,点
轴的非负半轴上,点 到短轴端点的距离是4,椭圆上的点到焦点
到短轴端点的距离是4,椭圆上的点到焦点 距离的最大值是6.
距离的最大值是6.
(Ⅰ)求椭圆的标准方程和离心率 ;
;
(Ⅱ)若 为焦点
为焦点 关于直线
关于直线 的对称点,动点
的对称点,动点 满足
满足 ,问是否存在一个定点
,问是否存在一个定点 ,使
,使 到点
到点 的距离为定值?若存在,求出点
的距离为定值?若存在,求出点 的坐标及此定值;若不存在,请说明理由.
的坐标及此定值;若不存在,请说明理由.
解: (Ⅰ)设椭圆长半轴长及半焦距分别为 ,由已知得
,由已知得
 .
.
所以椭圆的标准方程为 . 离心率
. 离心率
(Ⅱ) ,设
,设 由
由 得
得

化简得 ,即
,即
故存在一个定点 ,使
,使 到
到 点的距离为定值,其定值为
点的距离为定值,其定值为
107. [2010 •福建理数]已知中心在坐标原点O的椭圆C经过点A(2,3),且点F(2,0)为其右焦点。
(1)求椭圆C的方程;
(2)是否存在平行于OA的直线 ,使得直线
,使得直线 与椭圆C有公共点,且直线OA与
与椭圆C有公共点,且直线OA与 的距离等于4?若存在,求出直线
的距离等于4?若存在,求出直线 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
解:(1)依题意,可设椭圆C的方程为 ,且可知左焦点为
,且可知左焦点为

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com