
3.数列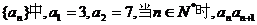 的个位数,则数列
的个位数,则数列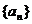 的第2010项是
的第2010项是
( )
A.1 B.3 C.9 D.7
2.已知抛物线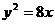 的焦点与双曲线
的焦点与双曲线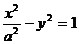 的一个焦点重合,则该双曲线的离心率为 ( )
的一个焦点重合,则该双曲线的离心率为 ( )
A.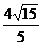 B.
B.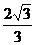 C.
C.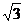 D.3
D.3
1.已知全集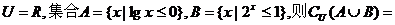 ( )
( )
A.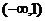 B.
B.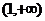 C.
C.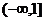 D.
D.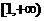
22.(本题满分12分)
已知可行域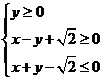 的外接圆
的外接圆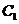 与
与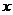 轴交于点
轴交于点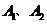 ,椭圆
,椭圆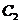 以线段
以线段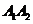 为长轴,离心率
为长轴,离心率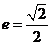
(1)求圆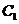 及椭圆
及椭圆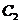 的方程;
的方程;
(2)设椭圆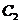 的右焦点为
的右焦点为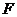 ,点
,点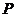 为圆
为圆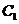 上异于
上异于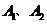 的动点,过原点
的动点,过原点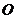 作直线
作直线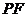 垂线交直线
垂线交直线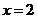 于点
于点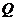 判断直线
判断直线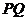 与圆
与圆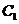 的位置关系,并给出证明.
的位置关系,并给出证明.




21.(本题满分12分)
已知函数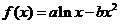 图象上一点
图象上一点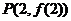 处的切线方程为
处的切线方程为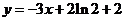 .
.
(1)求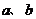 的值;
的值;
(2)若方程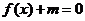 在
在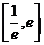 内有两个不等实根.求
内有两个不等实根.求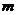 的取值范围(其中
的取值范围(其中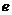 为自然对数的底数).
为自然对数的底数).
20.(本题满分12分)
已知公差大于零的等差数列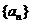 的前
的前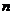 项和为
项和为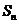 ,且满足:
,且满足: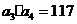 ,
,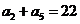 .
.
(1)求数列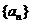 的通项公式
的通项公式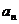 ;
;
(2)若数列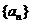 是等差数列,且
是等差数列,且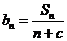 ,求非零常数
,求非零常数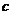 ;
;
(3)若(2)中的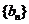 的前
的前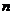 项和为
项和为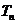 ,求证
,求证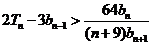
19.(本题满分12分)
-个多面体的直观图和三视图如图所示,其中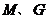 分别是
分别是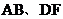 中点.
中点.
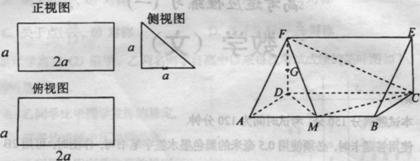
(1)求证: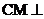 平面
平面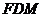 ;
;
(2)在线段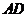 (含
(含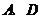 端点)确定一点
端点)确定一点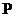 .使得
.使得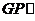 平面
平面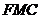 ,并给出证明.
,并给出证明.
18.(本题满分12分)
在甲、乙两个盒子中分别装有标号为1、2、3、4的四个球,现从甲、乙两个盒子中各取出1个球,每个小球被取出的可能性相等.
(1)求取出的两个球上标号为相邻整数的概率;
(2)求取出的两个球上标号之和能被3整除的概率.
17.(本题满分12分)
在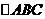 中,
中,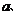
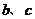 为角
为角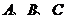 所对的三边.已知
所对的三边.已知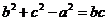
(1)求角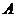 的值;
的值;
(2)若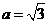 ,设内角
,设内角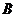 为
为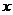 ,周长为
,周长为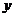 ,求
,求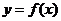 的最大值.
的最大值.
16.若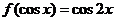 ,且
,且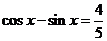 ,则
,则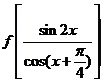 等于_______
等于_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com