
1. 结束[(+by/with)]
We concluded our meeting at 9 o’clock.
我们九点钟结束了会议。
22.(本题满分14分)
解:(Ⅰ) , …………2分
, …………2分
由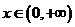 ,得,
,得,
当 时,
时,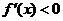 ,
, 单调递减;
单调递减;
当 时,
时,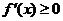 ,
, 单调递增. …………………………4分
单调递增. …………………………4分
∴ 当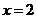 时,
时, 取得最小值
取得最小值 ,
,
即对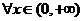 ,
, 常数
常数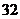 ,都有
,都有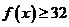 成立,
成立,
所以, 在
在 上有下界. ……………………………………………6分
上有下界. ……………………………………………6分
(Ⅱ)由 ,知
,知
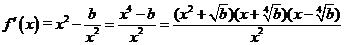 …………………8分
…………………8分
由 ,知
,知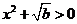 ,
, ,
,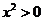
所以,当 ,即
,即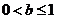 时,
时,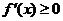 ,
, 在
在 上单调递增;
上单调递增;
 ,即
,即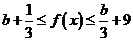 恒成立,
恒成立, 在
在 上是有界函数;
上是有界函数;
当 ,即
,即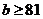 时,
时,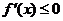 ,
, 在
在 上单调递减;
上单调递减;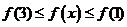 ,即
,即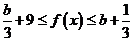 恒成立,
恒成立, 在
在 上是有界函数;………………11分
上是有界函数;………………11分
当 ,即
,即 时,有
时,有 在
在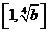 上单调递减;在
上单调递减;在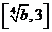 上单调递增,且
上单调递增,且 ,
,
从而当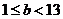 时,
时,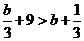 ,
,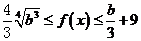 恒成立,
恒成立, 在
在 上是有界函数;
上是有界函数;
当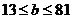 时,
时, ,
, 恒成立,
恒成立, 在
在 上是有界函数.
……………………………………………………………13分
上是有界函数.
……………………………………………………………13分
综上可知, 在
在 上是有界函数.
上是有界函数.
且当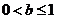 时,下界为
时,下界为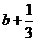 ;当
;当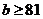 时,下界为
时,下界为 ;当
;当 时,下界为
时,下界为 . ………………………………………………………………………………14分
. ………………………………………………………………………………14分
21.(本题满分12分)
解:(Ⅰ)将
 得
得 
由 得
得 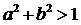
设 ,则
,则
 ,
,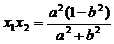 ①……………………………2分
①……………………………2分
∵
 ∴
∴ 
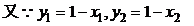
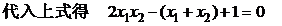 ②
②
将①代入②式,整理得:
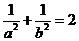 ……………………………4分
……………………………4分
∵ 
∴ 椭圆过四个定点:
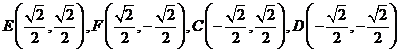 …5分
…5分
∵ 
∴ 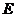 、
、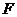 、
、 、
、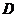 四点在圆
四点在圆 上. ……………………… 7分
上. ……………………… 7分
(Ⅱ)设椭圆 的右焦点为
的右焦点为 ,
,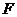 关于直线
关于直线 的对称点为
的对称点为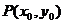 ,
,
则 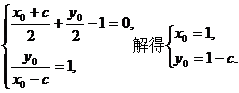 ……………………………8分
……………………………8分
∵  ∴
∴ 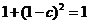 解得
解得 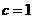 ……9分
……9分
由(I)得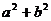 =
= 又
又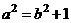
∴ 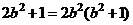 解得
解得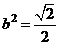 从而
从而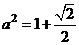
故所求椭圆方程为 . ………………………12分
. ………………………12分
20.(本题满分12分)
解:(Ⅰ) (元); …………………………………………3分
(元); …………………………………………3分
 (元).……………6分
(元).……………6分
(Ⅱ)因为 元可买某股票
元可买某股票 股,又6个月后每股价格为
股,又6个月后每股价格为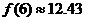 (元),所以,总盈利为
(元),所以,总盈利为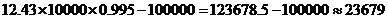 (元).
(元).
答:6个月后盈利为 元.……………………………………………………………12分
元.……………………………………………………………12分
19.(本题满分12分)
解:(Ⅰ)依题意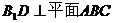 ,∴
,∴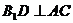
又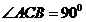 ,∴
,∴ ,
,
而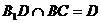 ,∴
,∴ 平面
平面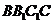 . ……………………………………………4分
. ……………………………………………4分
(Ⅱ)∵ ,
,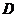 为
为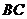 的中点,∴
的中点,∴
又 ∴在
∴在 中,
中, ,
,
而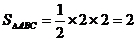 , ………………………………………………………………7分
, ………………………………………………………………7分
∴斜三棱柱 的体积
的体积 .……………………………8分
.……………………………8分
(Ⅲ)由(Ⅰ)知 平面
平面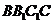 ,又
,又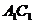 ∥
∥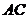 ∴
∴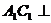 平面
平面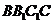 ,
,
∴四棱锥 的高
的高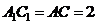
由(Ⅱ)知, ,
,
而 ,∴在
,∴在 中,
中,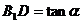 ,
,
∴底面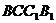 的面积
的面积 , ……………………………………10分
, ……………………………………10分
依题意: 四棱锥 的体积
的体积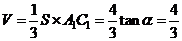 ,
,
∴ ,又
,又 ,∴
,∴  ,
,
于是,当 时,四棱锥
时,四棱锥 的体积为
的体积为 .………………………………12分
.………………………………12分
18.(本题满分12分)
解:(Ⅰ)从 各取一个数组成数对
各取一个数组成数对 共有
共有 对, ……………………………2分
对, ……………………………2分
其中满足 的有(6,4),(6,5),(7,3),(7,4),(7,5),(8,2),(8,3),(8,4),(8,5)共9对 ………………………………………………………4分
的有(6,4),(6,5),(7,3),(7,4),(7,5),(8,2),(8,3),(8,4),(8,5)共9对 ………………………………………………………4分
故所求的概率为 ………………………………………………………6分
………………………………………………………6分
(Ⅱ)用 作为拟合直线时,所得
作为拟合直线时,所得 值与
值与 的实际值的差的平方和为
的实际值的差的平方和为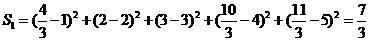 ……………8分
……………8分
用 作为拟合直线时,所得
作为拟合直线时,所得 值与
值与 的实际值的差的平方和为
的实际值的差的平方和为
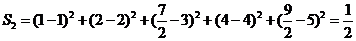 ………………10分
………………10分
∵ 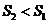 ,故用直线
,故用直线 拟合程度更好.
…………………………………12分
拟合程度更好.
…………………………………12分
17.(本题满分12分)
解:(Ⅰ) ,
,  ,
,
∴ . ……………………………………………1分
. ……………………………………………1分
又 , ∴
, ∴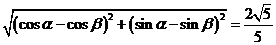 , …………3分
, …………3分
即  , ∴
, ∴ 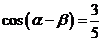 . …………………………5分
. …………………………5分
(Ⅱ)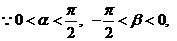 , ∴
, ∴ 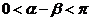
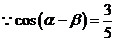 , ∴
, ∴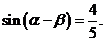 …………………………………………7分
…………………………………………7分
又 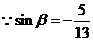 , ∴
, ∴ , …………………………………………9分
, …………………………………………9分
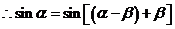

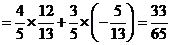 . …………………………………………12分
. …………………………………………12分
15. 16.①②③
16.①②③
13.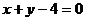 14.
14.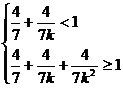
7.D 8. D 9.D 10.B 11.B 12.A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com