
9.函数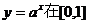 上的最大值与最小值的和为3,则
上的最大值与最小值的和为3,则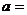 ( )
( )
A、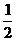 B、2 C、4 D、
B、2 C、4 D、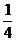
8.函数y=ax2+bx+3在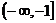 上是增函数,在
上是增函数,在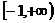 上是减函数,则 ( )
上是减函数,则 ( )
A、b>0且a<0 B、b=2a<0 C、b=2a>0 D、a,b的符号不定
7. 已知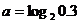 ,
,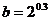 ,
,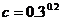 ,则
,则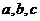 三者的大小关系是 ( )
三者的大小关系是 ( )
A、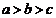 B、
B、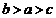 C、
C、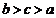 D、
D、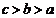
6.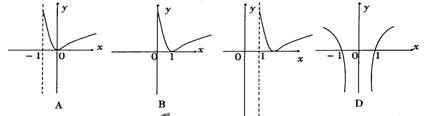 函数y= | lg(x-1)|
的图象是
( )
函数y= | lg(x-1)|
的图象是
( )
5、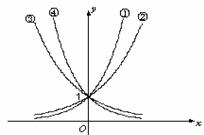 下图是指数函数1
下图是指数函数1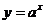 、2
、2 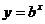 、3
、3 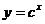 、4
、4 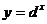 的图象,则
的图象,则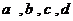 与1的大小关系是( )
与1的大小关系是( )
A.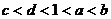 B.
B.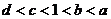
C.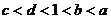 D.
D.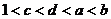
4.设f,g都是由A到A的映射,其对应法则如下表(从上到下):

则与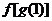 相同的是
(
)
相同的是
(
)
A.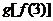 B.
B.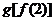 C.
C.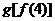 D.
D.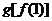
3.函数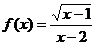 的定义域为
( )
的定义域为
( )
A、[1,2)∪(2,+∞) B、(1,+∞) C、[1,2) D、[1,+∞)
2.设A={a,b},集合B={a+1,5},若A∩B={2},则A∪B= ( )
A、{1,2} B、{1,5} C、{2,5} D、{1,2,5}
1、下列四个集合中,是空集的是( )
A
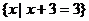 B
B
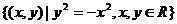
C
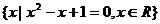 D
D
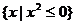
2、我舰在敌岛A南偏西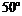 相距12海里的B处,发现敌舰正由岛沿北偏西
相距12海里的B处,发现敌舰正由岛沿北偏西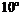 的方向以10海里/小时的速度航行.问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰?(角度用反三角函数表示)
的方向以10海里/小时的速度航行.问我舰需以多大速度、沿什么方向航行才能用2小时追上敌舰?(角度用反三角函数表示)
●板书设计
●授后记
课题: §2.2解三角形应用举例
授课类型:新授课
●教学目标
知识与技能:能够运用正弦定理、余弦定理等知识和方法进一步解决有关三角形的问题, 掌握三角形的面积公式的简单推导和应用
过程与方法:本节课补充了三角形新的面积公式,巧妙设疑,引导学生证明,同时总结出该公式的特点,循序渐进地具体运用于相关的题型。另外本节课的证明题体现了前面所学知识的生动运用,教师要放手让学生摸索,使学生在具体的论证中灵活把握正弦定理和余弦定理的特点,能不拘一格,一题多解。只要学生自行掌握了两定理的特点,就能很快开阔思维,有利地进一步突破难点。
情感态度与价值观:让学生进一步巩固所学的知识,加深对所学定理的理解,提高创新能力;进一步培养学生研究和发现能力,让学生在探究中体验愉悦的成功体验
●教学重点
推导三角形的面积公式并解决简单的相关题目
●教学难点
利用正弦定理、余弦定理来求证简单的证明题
●教学过程
Ⅰ.课题导入
[创设情境]
师:以前我们就已经接触过了三角形的面积公式,今天我们来学习它的另一个表达公式。在
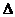 ABC中,边BC、CA、AB上的高分别记为h
ABC中,边BC、CA、AB上的高分别记为h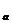 、h
、h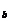 、h
、h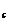 ,那么它们如何用已知边和角表示?
,那么它们如何用已知边和角表示?
生:h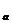 =bsinC=csinB
=bsinC=csinB
h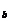 =csinA=asinC
=csinA=asinC
h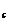 =asinB=bsinaA
=asinB=bsinaA
师:根据以前学过的三角形面积公式S=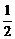 ah,应用以上求出的高的公式如h
ah,应用以上求出的高的公式如h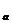 =bsinC代入,可以推导出下面的三角形面积公式,S=
=bsinC代入,可以推导出下面的三角形面积公式,S=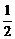 absinC,大家能推出其它的几个公式吗?
absinC,大家能推出其它的几个公式吗?
生:同理可得,S=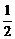 bcsinA, S=
bcsinA, S=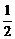 acsinB
acsinB
师:除了知道某条边和该边上的高可求出三角形的面积外,知道哪些条件也可求出三角形的面积呢?
生:如能知道三角形的任意两边以及它们夹角的正弦即可求解
Ⅱ.讲授新课
[范例讲解]
例1、在 ABC中,根据下列条件,求三角形的面积S(精确到0.1cm
ABC中,根据下列条件,求三角形的面积S(精确到0.1cm )
)
(1)已知a=14.8cm,c=23.5cm,B=148.5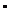 ;
;
(2)已知B=62.7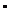 ,C=65.8
,C=65.8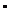 ,b=3.16cm;
,b=3.16cm;
(3)已知三边的长分别为a=41.4cm,b=27.3cm,c=38.7cm
分析:这是一道在不同已知条件下求三角形的面积的问题,与解三角形问题有密切的关系,我们可以应用解三角形面积的知识,观察已知什么,尚缺什么?求出需要的元素,就可以求出三角形的面积。
解:(1)应用S=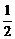 acsinB,得
acsinB,得
S=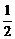
 14.8
14.8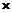 23.5
23.5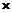 sin148.5
sin148.5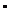 ≈90.9(cm
≈90.9(cm )
)
(2)根据正弦定理,
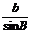 =
= 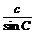
c = 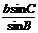
S = 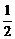 bcsinA =
bcsinA = 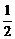 b
b
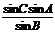
A = 180 -(B + C)= 180
-(B + C)= 180 -(62.7
-(62.7 + 65.8
+ 65.8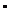 )=51.5
)=51.5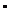
S = 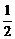
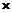 3.16
3.16
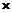
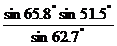 ≈4.0(cm
≈4.0(cm )
)
(3)根据余弦定理的推论,得
cosB =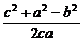
=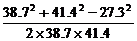
≈0.7697
sinB = 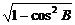 ≈
≈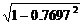 ≈0.6384
≈0.6384
应用S=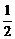 acsinB,得
acsinB,得
S ≈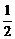
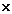 41.4
41.4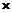 38.7
38.7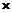 0.6384≈511.4(cm
0.6384≈511.4(cm )
)
例2、如图,在某市进行城市环境建设中,要把一个三角形的区域改造成室内公园,经过测量得到这个三角形区域的三条边长分别为68m,88m,127m,这个区域的面积是多少?(精确到0.1cm )?
)?
师:你能把这一实际问题化归为一道数学题目吗?
生:本题可转化为已知三角形的三边,求角的问题,再利用三角形的面积公式求解。
由学生解答,老师巡视并对学生解答进行讲评小结。
解:设a=68m,b=88m,c=127m,根据余弦定理的推论,
cosB=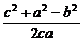
=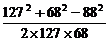 ≈0.7532
≈0.7532
sinB=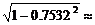 0.6578
0.6578
应用S=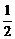 acsinB
acsinB
S ≈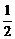
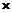 68
68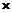 127
127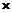 0.6578≈2840.38(m
0.6578≈2840.38(m )
)
答:这个区域的面积是2840.38m 。
。
例3、在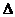 ABC中,求证:
ABC中,求证:
(1)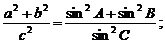
(2)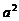 +
+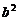 +
+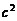 =2(bccosA+cacosB+abcosC)
=2(bccosA+cacosB+abcosC)
分析:这是一道关于三角形边角关系恒等式的证明问题,观察式子左右两边的特点,联想到用正弦定理来证明
证明:(1)根据正弦定理,可设
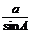 =
= 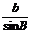 =
= 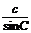 = k
= k
显然 k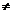 0,所以
0,所以
左边=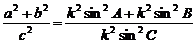
=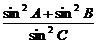 =右边
=右边
(2)根据余弦定理的推论,
右边=2(bc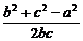 +ca
+ca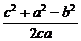 +ab
+ab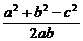 )
)
=(b +c
+c - a
- a )+(c
)+(c +a
+a -b
-b )+(a
)+(a +b
+b -c
-c )
)
=a +b
+b +c
+c =左边
=左边
变式练习1:已知在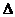 ABC中,
ABC中,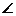 B=30
B=30 ,b=6,c=6
,b=6,c=6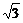 ,求a及
,求a及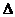 ABC的面积S
ABC的面积S
提示:解有关已知两边和其中一边对角的问题,注重分情况讨论解的个数。
答案:a=6,S=9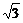 ;a=12,S=18
;a=12,S=18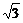
变式练习2:判断满足下列条件的三角形形状,
(1) acosA = bcosB
(2)
sinC =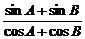
提示:利用正弦定理或余弦定理,“化边为角”或“化角为边”
(1) 师:大家尝试分别用两个定理进行证明。
生1:(余弦定理)得
a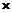
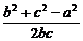 =b
=b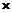
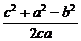
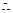 c
c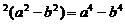 =
=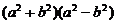
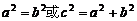
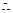 根据边的关系易得是等腰三角形或直角三角形
根据边的关系易得是等腰三角形或直角三角形
生2:(正弦定理)得
sinAcosA=sinBcosB,
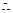 sin2A=sin2B,
sin2A=sin2B,
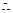 2A=2B,
2A=2B,
 A=B
A=B
 根据边的关系易得是等腰三角形
根据边的关系易得是等腰三角形
师:根据该同学的做法,得到的只有一种情况,而第一位同学的做法有两种,请大家思考,谁的正确呢?
生:第一位同学的正确。第二位同学遗漏了另一种情况,因为sin2A=sin2B,有可能推出2A与2B两个角互补,即2A+2B=180 ,A+B=90
,A+B=90
(2)(解略)直角三角形
Ⅲ.课堂练习
课本第21页练习第1、2题
Ⅳ.课时小结
利用正弦定理或余弦定理将已知条件转化为只含边的式子或只含角的三角函数式,然后化简并考察边或角的关系,从而确定三角形的形状。特别是有些条件既可用正弦定理也可用余弦定理甚至可以两者混用。
Ⅴ.课后作业
课本第23页练习第12、14、15题
●板书设计
●授后记
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com