
6.A、B、C、D是空间不共面的四点,且满足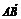 ·
· =0,
=0, ·
·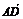 =0,
=0,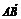 ·
·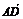 =0,则△BCD是 三角形(用“锐角”、“直角”、“钝角”填空).
=0,则△BCD是 三角形(用“锐角”、“直角”、“钝角”填空).
答案 锐角
5.已知A(4,1,3),B(2,-5,1),C为线段AB上一点,且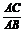 =
=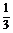 ,则C点的坐标为 .
,则C点的坐标为 .
答案 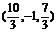
4.已知空间四边形ABCD的每条边和对角线的长都等于a,点E、F分别是BC、AD的中点,则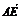 ·
·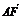 的值为 .
的值为 .
答案 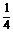 a2
a2
3.已知向量a,b满足|a|=2,|b|=3,|2a+b|=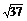 ,则a与b的夹角为
.
,则a与b的夹角为
.
答案 60°
2.已知向量a=(8,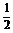 x,x)b=(x,1,2),其中x>0.若a∥b,则x的值为
.
x,x)b=(x,1,2),其中x>0.若a∥b,则x的值为
.
答案 4
1.已知点O、A、B、C为空间不共面的四点,且向量a=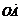 +
+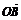 +
+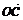 ,向量b=
,向量b=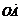 +
+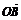 -
-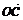 ,则
,则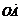 、
、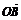 、
、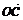 中不能与a,b构成空间基底的向量是 .
中不能与a,b构成空间基底的向量是 .
答案 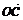
(17)(本小题满分12分)
设G是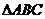 的重心(即三条中线的交点),
的重心(即三条中线的交点),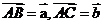 ,
,
(Ⅰ)试用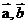 表示
表示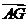 ;(Ⅱ)试用
;(Ⅱ)试用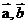 表示
表示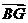
解:(Ⅰ)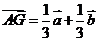 ----------------------------------(6分);
----------------------------------(6分);
(Ⅱ)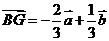 -----------------------------------(12分)
-----------------------------------(12分)
(18) (本小题满分12分)
已知函数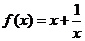
(Ⅰ)求证: 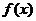 在区间
在区间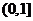 内单调递减,在
内单调递减,在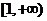 内单调递增;
内单调递增;
(Ⅱ)求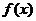 在区间
在区间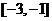 上的最小值.
上的最小值.
(Ⅰ)证明:设 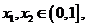 且
且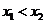 ,则
,则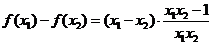
又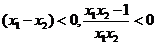
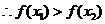
 区间
区间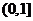 内单调递减,同理可证在
内单调递减,同理可证在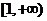 内单调递增;----------------------- (7分);
内单调递增;----------------------- (7分);
(Ⅱ)利用单调性的定义或奇函数的性质可知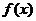 在区间
在区间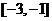 上单增,
上单增,
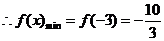 -----------------------------------------------------------------------------(12分)
-----------------------------------------------------------------------------(12分)
(19).(本小题满分12分)
已知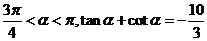
(Ⅰ)求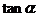 的值;
的值;
(Ⅱ)求的值.

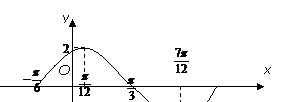 (20).(本小题满分12分)
(20).(本小题满分12分)
已知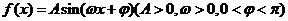
图象的一部分如图所示:
(1)求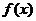 的解析式;(2)写出
的解析式;(2)写出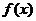 的单调区间.
的单调区间.
 (21).(本小题满分12分)
(21).(本小题满分12分)
舒城县某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出。当每辆车的月租金每增加50元时,未租出的车将会增加一辆。租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元。
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:(1)当每辆车的月租金定为3600时,未租出的车辆数为: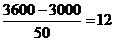 ,所以这时租出了88辆车。--------------------------------------------------------------------------------------------------------------- (4分);
,所以这时租出了88辆车。--------------------------------------------------------------------------------------------------------------- (4分);
(2)设每辆本的月租金定为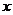 元,则租赁公司的月收益为:
元,则租赁公司的月收益为: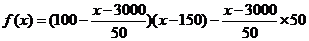 ,
,
整理得: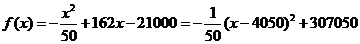 。所以,当
。所以,当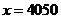 时,
时,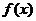 最大,其最大值为
最大,其最大值为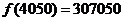 。即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元。--------------------------------------------------------------------------------------------------- (12分);
。即当每辆车的月租金定为4050元时,租赁公司的月收益最大,最大收益为307050元。--------------------------------------------------------------------------------------------------- (12分);
(22).(本小题满分14分)
已知: 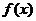 是定义在
是定义在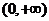 上的函数,且①
上的函数,且①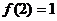 ,②对
,②对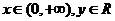 ,恒有
,恒有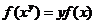 ③
③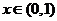 时,有
时,有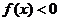
(Ⅰ)求证: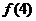 =2;
=2;
(Ⅱ)求证: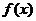 在
在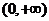 上单调递增。
上单调递增。
(Ⅲ)若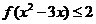 ,求
,求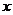 的取值范围。(提示:注意利用已证结论)
的取值范围。(提示:注意利用已证结论)
(13) 函数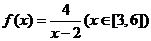 的值域为
。
的值域为
。
答案: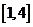

(14) 函数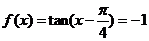 ,则
,则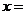 。
。
答案: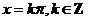
(15) 已知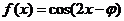
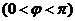 的图像关于直线
的图像关于直线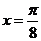 对称,则
对称,则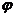 =
。
=
。
答案: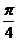
 (16) 设
(16) 设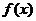 是R上的奇函数,且在
是R上的奇函数,且在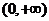 内是增函数,又
内是增函数,又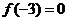 ,则
,则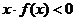 的解集是
。
的解集是
。
答案: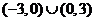
(1) 已知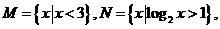 则
则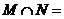 (
D )
(
D )
A.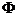 B.
B.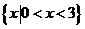 C.
C.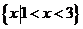 D.
D.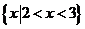

(2) 化简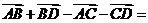 (
D )
(
D )
A.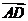 B.
B.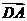 C.
C.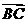 D.
D.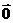 .
.
(3) 已知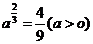 ,则
,则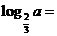 ( C
)
( C
)
A.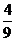 B.
B.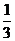 C.
C.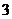 D.
D.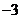

(4) 函数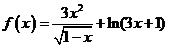 的定义域为
( B )
的定义域为
( B )
A.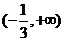 B.
B.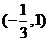
 C.
C.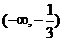 D.
D.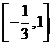

(5) 设已知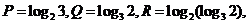 则 ( A )
则 ( A )
A.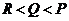 B.
B.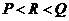 C.
C.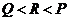 D.
D.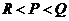

(6) 已知点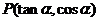 在第三象限,则角
在第三象限,则角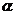 的终边位置在
( B )
的终边位置在
( B )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
(7) 若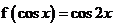 ,则
,则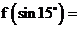 ( A )
( A )
A.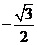 B.
B.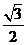 C.
C.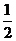 D.
D.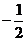

(8) 为了得到函数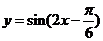 的图像,可以将函数
的图像,可以将函数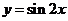 的图像 ( B )
的图像 ( B )
A.向右平移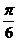 个单位
B.向右平移
个单位
B.向右平移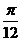 个单位
个单位 
C.向左平移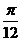 个单位 D.向右平移
个单位 D.向右平移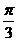 个单位
个单位
(9) 若函数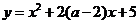 在区间
在区间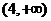 上是增函数,则
上是增函数,则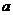 的取值范围是( B )
的取值范围是( B )
A.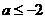 B.
B.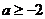 C.
C.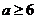 D.
D.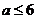

(10) 要使函数 的图像不经过第二象限,则
的图像不经过第二象限,则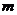 的取值范围是
(
A )
的取值范围是
(
A )
A.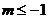 B.
B.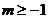 C.
C.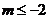 D.
D.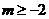

(11) 依据“二分法”,函数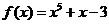 的实数解落在的区间是
(
B )
的实数解落在的区间是
(
B )
A.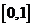 B.
B.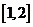 C.
C.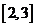 D.
D.

(12) 定义在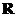 上的函数
上的函数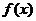 既是奇函数,又是周期函数,
既是奇函数,又是周期函数,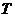 是它的一个正周期
是它的一个正周期 若将方程
若将方程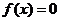 在闭区间
在闭区间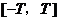 上的根的个数记为
上的根的个数记为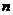 ,则
,则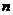 可能为
( D
)
可能为
( D
)
(提示:解选择题有诸多技巧。比如:排除法、一般问题特殊化等)
A 0 B
0 B 1 C
1 C 3 D
3 D 5
5
23.(本小题满分10分)已知f(x)是定义域为(0,+∞)的函数,当x∈(0,1)时,
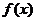 <0.现针对任意正实数x、y,给出下列四个等式:
<0.现针对任意正实数x、y,给出下列四个等式:
① 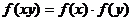 ;
②
;
② 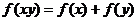 ;
;
③
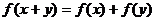 ; ④
; ④ 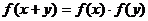 .
.
请选择其中的一个等式作为条件,使得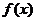 在(0,+∞)上为增函数.并证明你的结论.
在(0,+∞)上为增函数.并证明你的结论.
解:你所选择的等式代号是 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com