
2.一般数学表达式:
1.定律内容:相互作用的几个物体组成的系统,如果不受外力作用,或者它们受到的外力之和为零,则系统的总动量保持不变。
23.(09重庆卷)(16分)2009年中国女子冰壶队首次获得了世界锦标赛冠军,这引起了人们对冰壶运动的关注。冰壶在水平冰面上的一次滑行可简化为如下过程:如题23图,运动员将静止于O点的冰壶(视为质点)沿直线 推到A点放手,此后冰壶沿
推到A点放手,此后冰壶沿 滑行,最后停于C点。已知冰面各冰壶间的动摩擦因数为,冰壶质量为m,AC=L,
滑行,最后停于C点。已知冰面各冰壶间的动摩擦因数为,冰壶质量为m,AC=L, =r,重力加速度为g
=r,重力加速度为g

(1)求冰壶在A 点的速率;
(2)求冰壶从O点到A点的运动过程中受到的冲量大小;
(3)若将 段冰面与冰壶间的动摩擦因数减小为
段冰面与冰壶间的动摩擦因数减小为 ,原只能滑到C点的冰壶能停于
,原只能滑到C点的冰壶能停于 点,求A点与B点之间的距离。
点,求A点与B点之间的距离。
解析:
(1)对冰壶,从A点放手到停止于C点,设在A点时的速度为V1,
应用动能定理有-μmgL= mV12,解得V1=
mV12,解得V1= ;
;
(2)对冰壶,从O到A,设冰壶受到的冲量为I,
应用动量定理有I=mV1-0,解得I=m ;
;
(3)设AB之间距离为S,对冰壶,从A到O′的过程,
应用动能定理,-μmgS-0.8μmg(L+r-S)=0- mV12,
mV12,
解得S=L-4r。
(09山东卷)(2)如图所示,光滑水平面轨道上有三个木块,A、B、C,质量分别为mB=mc=2m,mA=m,A、B用细绳连接,中间有一压缩的弹簧 (弹簧与滑块不栓接)。开始时A、B以共同速度v0运动,C静止。某时刻细绳突然断开,A、B被弹开,然后B又与C发生碰撞并粘在一起,最终三滑块速度恰好相同。求B与C碰撞前B的速度。
(2)设共同速度为v,球A和B分开后,B的速度为 ,由动量守恒定律有
,由动量守恒定律有 ,
, ,联立这两式得B和C碰撞前B的速度为
,联立这两式得B和C碰撞前B的速度为 。
。
[考点]原子核、动量守恒定律
一:复习要点
25. (16分)
(16分)
(09福建卷) (1)现代科学技术的发展与材料科学、能源的开发密切相关,下列关于材料、能源的说法正确的是
。(填选项前的编号)
(1)现代科学技术的发展与材料科学、能源的开发密切相关,下列关于材料、能源的说法正确的是
。(填选项前的编号)
 ①化石能源为清洁能源
②纳米材料的粒度在1-100μm之间
①化石能源为清洁能源
②纳米材料的粒度在1-100μm之间
 ③半导体材料的导电性能介于金属导体和绝缘体之间
③半导体材料的导电性能介于金属导体和绝缘体之间
 ④液晶既有液体的流动性,又有光学性质的各向同性
④液晶既有液体的流动性,又有光学性质的各向同性
[解析](1)化石能源燃烧时产生二氧化碳,造成温室气体效应;煤碳和石油中含有硫,燃烧时产生二氧化硫等物质使雨水的酸度增高等等,说明化石能源不是清洁能源;①错;
纳米材料的粒度在1-100nm,而不是1-100μm,②错;
液晶既有液体的流动性,又有光学性质的各向异性(不是同性),④错。
正确选项为③
24.(1)设碰撞前的速度为,根据机械能守恒定律
 ①
①
设碰撞后m1与m2的速度分别为v1和v2,根据动量守恒定律
 ②
②
由于碰撞过程中无机械能损失
 ③
③
②、③式联立解得
 ④
④
将①代入得④

(2)a由④式,考虑到 得
得
根据动能传递系数的定义,对于1、2两球
 ⑤
⑤
同理可得,球m2和球m3碰撞后,动能传递系数k13应为
 ⑥
⑥
依次类推,动能传递系数k1n应为

解得

b.将m1=4m0,m3=mo代入⑥式可得

为使k13最大,只需使
由

24.(09北京卷)(20分) 如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为
如图1所示,ABC为一固定在竖直平面内的光滑轨道,BC段水平,AB段与BC段平滑连接。质量为 的小球从高位
的小球从高位 处由静止开始沿轨道下滑,与静止在轨道BC段上质量为
处由静止开始沿轨道下滑,与静止在轨道BC段上质量为 的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球
的小球发生碰撞,碰撞后两球两球的运动方向处于同一水平线上,且在碰撞过程中无机械能损失。求碰撞后小球 的速度大小
的速度大小 ;
;
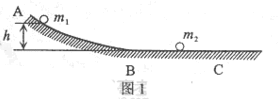
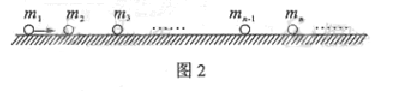
(2)碰撞过程中的能量传递规律在屋里学中有着广泛的应用。为了探究这一规律,我们才用多球依次碰撞、碰撞前后速度在同一直线上、且无机械能损失的恶简化力学模型。如图2所示,在固定光滑水平轨道上,质量分别为 、
、 ……的若干个球沿直线静止相间排列,给第1个球初能
……的若干个球沿直线静止相间排列,给第1个球初能 ,从而引起各球的依次碰撞。定义其中第
,从而引起各球的依次碰撞。定义其中第 个球经过依次碰撞后获得的动能
个球经过依次碰撞后获得的动能 与
与 之比为第1个球对第
之比为第1个球对第 个球的动能传递系数
个球的动能传递系数
a 求
b 若 为确定的已知量。求
为确定的已知量。求 为何值时,
为何值时, 值最大
值最大
[解析]
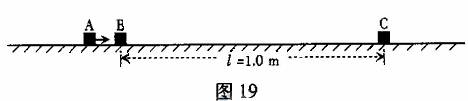
19.(09广东物理卷)(16分)如图19所示,水平地面上静止放置着物块B和C,相距 =1.0m 。物块A以速度
=1.0m 。物块A以速度 =10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度
=10m/s沿水平方向与B正碰。碰撞后A和B牢固地粘在一起向右运动,并再与C发生正碰,碰后瞬间C的速度 =2.0m/s 。已知A和B的质量均为m,C的质量为A质量的k倍,物块与地面的动摩擦因数
=2.0m/s 。已知A和B的质量均为m,C的质量为A质量的k倍,物块与地面的动摩擦因数 =0.45.(设碰撞时间很短,g取10m/s2)
=0.45.(设碰撞时间很短,g取10m/s2)
(1)计算与C碰撞前瞬间AB的速度;
(2)根据AB与C的碰撞过程分析k的取值范围,并讨论与C碰撞后AB的可能运动方向。
[解析]⑴设AB碰撞后的速度为v1,AB碰撞过程由动量守恒定律得 
设与C碰撞前瞬间AB的速度为v2,由动能定理得 
联立以上各式解得
⑵若AB与C发生完全非弹性碰撞,由动量守恒定律得 
代入数据解得 
此时AB的运动方向与C相同
若AB与C发生弹性碰撞,由动量守恒和能量守恒得

联立以上两式解得
代入数据解得 
此时AB的运动方向与C相反
若AB与C发生碰撞后AB的速度为0,由动量守恒定律得
代入数据解得
总上所述得 当 时,AB的运动方向与C相同
时,AB的运动方向与C相同
当 时,AB的速度为0
时,AB的速度为0
当 时,AB的运动方向与C相反
时,AB的运动方向与C相反
23.(16分)
解:
(1) 设起重机允许输出的最大功率为P0,重物达到最大速度时,拉力F0等于重力。
P0=F0 m
①
m
①
P0=mg ②
代入数据,有:P0=5.1×104W ③
说明:①式2分,②③式各1分。
(2) 匀加速运动结束时,起重机达到允许输出的最大功率,设此时重物受到的拉力为F,速度为v1,匀加速运动经历时间为t1,有:
P0=Fv1 ④
F-mg=ma ⑤
V1=at1 ⑥
由③④⑤⑥,代入数据,得:t1=5 s ⑦
t=2 s时,重物处于匀加速运动阶段,设此时速度为v2,输出功率为P,则
 =at
⑧
=at
⑧
P=F ⑨
⑨
由⑤⑧⑨,代入数据,得:P=2.04×104W ⑩
说明④⑤⑥⑦⑧⑨式各2分,⑦⑩式各1分。
23.(09四川卷)(16分)
 图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上作匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动。取g=10 m/s2,不计额外功。求:
图示为修建高层建筑常用的塔式起重机。在起重机将质量m=5×103 kg的重物竖直吊起的过程中,重物由静止开始向上作匀加速直线运动,加速度a=0.2 m/s2,当起重机输出功率达到其允许的最大值时,保持该功率直到重物做vm=1.02 m/s的匀速运动。取g=10 m/s2,不计额外功。求:
(1) 起重机允许输出的最大功率。
(2) 重物做匀加速运动所经历的时间和起重机在第2秒末的输出功率。
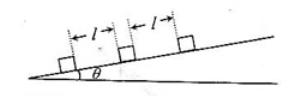
25.(09全国Ⅰ卷)(18分) 如图所示,倾角为θ的斜瓶上静止释放,质量均为m的木箱,相邻两木箱的距离均为l。工人用沿斜面的力推最小面的木箱使之上滑,逐一与其它木箱碰撞。每次碰撞后木箱都站在一起运动。整个过程中工人的推力不变,最后恰好能推着三个木箱匀速上滑。已知木箱与斜面向的动摩擦因数为p,重力加速度为g.设碰撞时间极短,求
(1)
 工人的推力;
工人的推力;
(2) 三个木箱均速运动的速度;
(3) 碰撞中损失的机械能。
答案(1)
(2)
(3)
[解析](1)当匀速时,把三个物体看作一个整体受重力、推力F、摩擦力f和支持力.根据平衡的知识有
(2)第一个木箱与第二个木箱碰撞之前的速度为V1,加速度 根据运动学公式或动能定理有
根据运动学公式或动能定理有 ,碰撞后的速度为V2根据动量守恒有
,碰撞后的速度为V2根据动量守恒有 ,即碰撞后的速度为
,即碰撞后的速度为 ,
,
然后一起去碰撞第三个木箱,设碰撞前的速度为V3
从V2到V3的加速度为 ,
,
根据运动学公式有 ,得
,得 ,
,
跟第三个木箱碰撞根据动量守恒有 ,
,
得 就是匀速的速度.
就是匀速的速度.
(3)设第一次碰撞中的能量损失为 ,根据能量守恒有
,根据能量守恒有 ,带入数据得
,带入数据得 .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com